Язык логики высказываний Пропозициональная логика

Привет, мой друг, тебе интересно узнать все про пропозициональная логика, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое пропозициональная логика, язык логики высказываний , логика высказываний , символическая логика , настоятельно рекомендую прочитать все из категории Модели представления знаний.

логика высказываний , пропозициональная логика (лат. propositio — «высказывание» ) или исчисление высказываний , также логика нулевого порядка — это раздел символической логики, изучающий сложные высказывания, образованные из простых, и их взаимоотношения. В отличие от логики предикатов, пропозициональная логика не рассматривает внутреннюю структуру простых высказываний, она лишь учитывает, с помощью каких союзов и в каком порядке простые высказывания сочленяются в сложные .Логика высказываний, пропозициональная логика (лат. propositio — «высказывание») или исчисление высказываний, также логика нулевого порядка — это раздел символической логики, изучающий сложные высказывания, образованные из простых, и их взаимоотношения.

Несмотря на свою важность и широкую сферу применения, логика высказываний является простейшей логикой и имеет очень ограниченные средства для исследования суждений .

символическая логика — это раздел формальной логики, в которой логические выводы исследуются посредством логических исчислений на основе строгого символического языка.

Основы современной логической символики были разработаны итальянским математиком Дж. Пеано, чьи интересы, как и Фреге, концентрировались вокруг оснований математики и развития формально-логического языка. Его широко известный труд «Formulaire de mathématiques», опубликованный (в соавторстве) в 1894–1908 годах, был нацелен на развитие математики в ее целостности, исходя из некоторых фундаментальных постулатов. Логическая запись Пеано была принята, хотя и частично модифицирована, А. Н. Уайтхедом и Б. Расселом в их широко известной трехтомной работе «Principia Mathematica» (1910–1913), а затем воспринята Д. Гилбертом. Таким образом, был введен в употребление символический язык, где появляются логические знаки:

• отрицания: ¬
• конъюнкции: &
• дизъюнкции: ∨
• импликации: ⊃
• кванторов всеобщности: ∀
• кванторов существования: ∃

Создание такого искусственного языка и с его помощью таких объектов, как логические исчисления, строго формализующие различные теории в виде некоторого конечного списка аксиом и правил вывода, означало, что в науке XIX века возникла потребность в символической логике. В первую очередь это было вызвано потребностями математики, ставившей проблемы, для решения которых средства традиционной логики были непригодны. Одной из таких проблем была недоказуемость пятого постулата Евклида из остальных постулатов и аксиом в его геометрии. Только с развитием символической логики появился аппарат, позволяющий решать проблему независимости аксиом данной теории чисто логическими средствами.

Основным стимулом развития символической логики в начале XX века была проблема оснований математики. К. Вейерштрасс, Р. Дедекинд и Г. Кантор показали, что в качестве фундамента всей классической математики может рассматриваться арифметика целых чисел. Дедикинд и Пеано аксиоматизировали арифметику, а Фреге дал определение натурального числа как множества всех равномощных множеств. Таким образом, вся математика сводилась к теории множеств. Однако в 1902 году математический мир был потрясен простотой и глубиной парадокса, обнаруженного Расселом в первом томе «Оснований арифметики» (Grundgesetze der Arithmetik) Фреге (основной закон V).

Ответом на этот и на другие парадоксы теории множеств стало возникновение четырех направлений в основаниях математики:

1. Логицизм (вся математика может быть дедуцирована из чистой логики без использования каких-либо специфических понятий, таких, как число или множество).
2. Интуиционизм (нужна новая логика).
3. Теоретико-множественный платонизм в виде аксиоматической теории множеств ZF (вводятся ограничения на образование множеств).
4. Формализм (программа Гилберта).

Доказательство существования бога по Гѐделю

язык логики высказываний

Язык логики высказываний (пропозициональный язык ) — формализованный язык, предназначенный для анализа логической структуры сложных высказываний .

Алфавит языка логики высказываний

Исходные символы, или алфавит языка логики высказываний, разделены на следующие три категории :

• пропозициональные буквы (пропозициональные переменные):

• логические знаки (логические союзы):

Символ	Значение
	Знак отрицания
или &	Знак конъюнкции («И»)
	Знак дизъюнкции («включающее ИЛИ»)
или	Знак строгой дизъюнкции («исключающее ИЛИ»)
	Знак импликации
или ~ или	Знак эквивалентности

Пропозициональные переменные

Пропозициональная переменная — переменная, которая в пропозициональных формулах служит для замены собой элементарных логических высказываний .

Пропозициональные формулы

Роль структурных образований, аналогичных элементарным и сложным высказываниям, играют в этом языке формулы. Пропозициональная формула — слово языка логики высказываний , т.е. конечная последовательность знаков алфавита, построенная по изложенным ниже правилам и образующая законченное выражение языка логики высказываний . Заглавные латинские буквы , и другие, которые употребляются в определении формулы, принадлежат не языку логики высказываний, а его метаязыку, то есть языку, который используется для описания самого языка логики высказываний. Содержащие метабуквы выражения , и другие — не пропозициональные формулы, а схемы формул. Например, выражение есть схема, под которую подходят формулы , и другие .

Индуктивное определение формулы логики высказываний:

1. пропозициональная переменная есть формула;
2. если — произвольная формула, то — тоже формула;
3. если и — произвольные формулы, то , , , и — тоже формулы.

Других формул в языке логики высказываний нет.

Относительно любой последовательности знаков алфавита языка логики высказываний можно решить, является она формулой или нет. Если эта последовательность может быть построена в соответствии с пп. 1—3 определения формулы, то она формула, если нет, то не формула .

Соглашения о скобках

Поскольку в построенных по определению формулах оказывается слишком много скобок, иногда и не обязательных для однозначного понимания формулы, математики приняли соглашения о скобках, по которым некоторые из скобок можно опускать. Об этом говорит сайт https://intellect.icu . Записи с опущенными скобками восстанавливаются по следующим правилам.

• Если опущены внешние скобки, то они восстанавливаются.
• Если рядом стоят две конъюнкции или дизъюнкции (например, ), то в скобки заключается сначала самая левая часть (то есть две подформулы со связкой между ними). (Говорят также, что эти связки левоассоциативны.)
• Если рядом стоят разные связки, то скобки расставляются согласно приоритетам: и (от высшего к низшему).

Когда говорят о длине формулы, имеют в виду длину подразумеваемой (восстанавливаемой) формулы, а не сокращенной записи.

Например: запись означает формулу , а ее длина равна 12.

Формализация и интерпретация

Как и любой другой формализованный язык, язык логики высказываний можно рассматривать как множество всех слов, построенных с использованием алфавита этого языка . Язык логики высказываний можно рассматривать как множество всевозможных пропозициональных формул . Предложения естественного языка могут быть переведены на символический язык логики высказываний, где они будут представлять собой формулы логики высказываний. Процесс перевода высказывания в формулу языка логики высказываний называется формализацией. Обратный процесс подстановки вместо пропозициональных переменных конкретных высказываний называется интерпретацией .

Аксиомы и правила вывода формальной системы логики высказываний

Одним из возможных вариантов (гильбертовской) аксиоматизации логики высказываний является следующая система аксиом:

;

;

;

;

;

;

;

;

;

;

.

вместе с единственным правилом:

(Modus ponens)

Теорема корректности исчисления высказываний утверждает, что все перечисленные выше аксиомы являются тавтологиями, а с помощью правила modus ponens из истинных высказываний можно получить только истинные. Доказательство этой теоремы тривиально и сводится к непосредственной проверке. Куда более интересен тот факт, что все остальные тавтологии можно получить из аксиом с помощью правила вывода — это так называемая теорема полноты логики высказываний.

Таблицы истинности основных операций

Основной задачей логики высказываний является установление истинностного значения формулы, если даны истинностные значения входящих в нее переменных. Истинностное значение формулы в таком случае определяется индуктивно (с шагами, которые использовались при построении формулы) с использованием таблиц истинности связок .

Пусть — множество всех истинностных значений , а — множество пропозициональных переменных. Тогда интерпретацию (или модель) языка логики высказываний можно представить в виде отображения

,

которое каждую пропозициональную переменную сопоставляет с истинностным значением .

Оценка отрицания задается таблицей:

Значения двухместных логических связок (импликация), (дизъюнкция) и (конъюнкция) определяются так:

Тождественно истинные формулы (тавтологии)

Формула является тождественно истинной, если она истинна при любых значениях входящих в нее переменных (то есть, при любой интерпретации)^[10]. Далее перечислены несколько широко известных примеров тождественно истинных формул логики высказываний:

• законы де Моргана:

;

;

• закон контрапозиции:

;

• законы поглощения:

;

;

• законы дистрибутивности:

;

.

Пропозициональная логика

В данном разделе рассматриваются стандартные шаблоны логического вывода, которые могут применяться для формирования цепочек заключений, ведущих к желаемой цели. Эти шаблоны логического вывода называются правилами логического вывода. Наиболее широко известное правило называется правилом отделения (Modus Ponens — модус поненс) и записывается следующим образом:

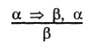
Эта запись означает, что если даны любые высказывания в форме α => β и а, то из них можно вывести высказывание β. Например, если дано (WumpusAhead ^ WumpusAlive) => Shoot и (WumpusAhead л WumpusAlive), то можно вывести высказывание Shoot.

Еще одним полезным правилом логического вывода является правило удаления связки "И", в котором утверждается, что из конъюнкции можно вывести любой из ее конъюнктов:

Например, из высказывания (WumpusAhead ^ WumpusAlive) можно вывести высказывание WumpusAlive. Рассматривая возможные истинностные значения α и β, можно легко показать, что правило отделения и правило удаления связки "И" являются непротиворечивыми не только применительно к данным примерам, но и ко всем возможным высказываниям. Это означает, что данные правила могут использоваться во всех конкретных случаях, в которых они могут потребоваться, вырабатывая непротиворечивые логические выводы без необходимости перебирать все модели.

В качестве правил логического вывода можно также применять все логические эквивалентности, приведенные в листинге. Например, из эквивалентности двухсторонней импликации и двух импликаций можно получить следующие два правила логического вывода (первое из них называется правилом удаления двухсторонней импликации):

Но не все правила логического вывода действуют в обоих направлениях, как это. Например, нельзя применить правило отделения в противоположном направлении, чтобы получить высказывания α => β и а из высказывания β.

Рассмотрим, как можно использовать эти правила логического вывода и эквивалентности в мире вампуса. Начнем с базы знаний, содержащей высказывания R₁—R₅, и покажем, как доказать высказывание ¬P_1,2, т.е. утверждение, что в квадрате [1,2] нет ямы. Вначале применим правило удаления двухсторонней импликации к высказыванию R₂, чтобы получить следующее:

R₆: (B_1,1 => (P_1,2 v P_2,1)) ^ ((P_1,2 v P_2,1) => B_1,1)

Затем применим к высказыванию R₆ правило удаления связки "И" и получим:

R7: ((P_1,2 v P_2,1) => B_1,1)

Из логической эквивалентности отрицаний следует:

R₈: (¬B_1,1 => ¬(P_1,2 v P_2,1))

Теперь можно применить правило отделения к высказыванию R₈ и к высказыванию R₄с данными восприятия (т.е. ¬B_1,1), чтобы получить следующее:

R9: ¬(P_1,2 v P_2,1)

Наконец, применим правило де Моргана, позволяющее получить такое заключение:

R10: ¬P_1,2 ^ ¬P_2,1

Это означает, что ни в квадрате [1,2],ни в квадрате [2,1] нет ямы.

Приведенный выше процесс логического вывода (последовательность применения правил логического вывода) называется доказательством. Процесс формирования доказательств полностью аналогичен процессу обнаружения решений в задачах поиска. В действительности, если можно было бы составить функцию определения преемника для выработки всех возможных вариантов применения правил логического вывода, это позволило бы использовать для формирования доказательств всеалгоритмы поиска. Таким образом, вместо трудоемкого перебора моделей может применяться более эффективный способ логического вывода — формирование доказательств. Поиск может проходить в прямом направлении, от первоначальной базы знаний, и осуществляться путем использования правил логического вывода для получения целевого высказывания, или же этот поиск может проходить в обратном направлении, от целевого высказывания, в попытке найти цепочку правил логического вывода, ведущую от первоначальной базы знаний. Ниже в этом разделе рассматриваются два семейства алгоритмов, в которых используются оба эти подхода.

Из того факта, что задача логического вывода в пропозициональной логике являетсяNP-полной, следует, что в наихудшем случае поиск доказательств может оказаться не более эффективным по сравнению с перебором моделей. Однако во многих практических случаях поиск доказательства может быть чрезвычайно эффективным просто потому, что в нем могут игнорироваться не относящиеся к делу (нерелевантные) высказывания, независимо от того, насколько велико их количество.

Например, в приведенном выше доказательстве, ведущем к высказыванию ¬P_1,2 ^ ¬P_2,1 не упоминались высказывания B_2,1, P_1,1, P_2,2 или P_3,1. Их можно было не рассматривать, поскольку целевое высказывание, P_1,2, присутствует только в высказывании R₄; остальные высказывания из состава R₄ присутствуют только в R₄ иR₂, поэтому R₁, R₃ и R₅ не имеют никакого отношения к доказательству. Те же рассуждения останутся справедливыми, если в базу знаний будет введено на миллион больше высказываний; с другой стороны, в этом случае простой алгоритм перебора строк в истинностной таблице был бы буквально подавлен из-за экспоненциального взрыва, вызванного стремительным увеличением количества моделей.

Это свойство логических систем фактически вытекает из гораздо более фундаментального свойства, называемого монотонностью. Согласно этому свойству, множество высказываний, которые могут быть получены путем логического вывода, возрастает лишь по мере добавления к базе знаний новой информации. Для любых высказываний α и β справедливо следующее:

если KB ≠ α, то KB ^ β ≠ α

Например, предположим, что база знаний содержит дополнительное утверждение β, согласно которому в этом экземпляре мира вампуса имеется точно восемь ям. Эти знания могут помочь агенту прийти к дополнительным заключениям, но не способны поставить под сомнение какое-либо уже сделанное заключение α, в частности вывод о том, что в квадрате [1,2] нет ямы. Монотонность означает, что правила логического вывода могут применяться каждый раз, когда в базе знаний обнаруживаются подходящие предпосылки, — полученное заключение будет следствием из данного правила, независимо от того, что еще находится в базе знаний.

пример

Курт Гедель

Философ науки и математик Курт Гедель предоставил формальные аргументы существования Бога. Его аргументы были опубликованы намного позже, после его смерти. Он привел аргументы, основанные на модальной логике; он использовал концепцию свойств, которые в итоге приводят к существованию Бога

Определение 1: «x» является богоподобным, тогда и только тогда, когда все его существенные свойства и только они положительны.

Определение 2: «А» является сущностью «x» тогда и только тогда, когда каждое свойство «B» объекта «X» является следствием «А». .

Определение 3: «X» обязательно существует тогда и только тогда, когда все его сущности воплощены.

Аксиома 1: Если свойство положительно, то его обратное не является положительным. .

Аксиома 2: Любое свойство, вызванное, т.е. прямо следующее из положительного, является положительным. .

Аксиома 3: Свойства Богоподобности всегда положительные .

Аксиома 4: Если свойство положительное, то оно обязательно положительное. .

Аксиома 5: Существование — положительное свойство

Аксиома 6: Для любого свойства P, если P положительно, то обязательно быть P - положительно.

Теорема 1: Если свойство положительно, то это можно доказать. .

Вывод 1: Свойство быть подобным Богу непротиворечиво. .

Теорема 2: Если что-то Богоподобное, то оно должно существовать. .

Теорема 3: Обязательно, свойство быть богоподобным воплощается. .

Гедель объяснил термин «богоподобный», как имеющий только положительные свойства. Он оставил термин «позитивный» неопределенным. Гедель считал, что это понимается как эстетическое и нравственное чувство, как противоположность лишения (отсутствие необходимых качеств во Вселенной). Он говорил, что «положительный» не стоит трактовать как эстетически «хорошо», так как понятие «хорошо» растяжимо и включает в себя и негативные характеристики. Вместо этого, он предположил, что «положительный» следует интерпретировать как совершенство или «исключительно хорошо», без отрицательных характеристик.^[28]

Гедель писал теоремы, опираясь на аксиомы, поэтому основная часть критики фокусировалась на его аксиомах и допущениях. Некоторые философы подвергали критике его основы модальной логики, когда другие критиковали его широкое понятие свойств. Оппи говорил, что Гедель так и не дал определения «положительным свойствам». Он предположил, что если эти положительные свойства образуют множество, то нет причин полагать, что любое такое существующее множество теологически интересно, или, что есть только один набор положительных свойств, которые теологически интересны.^[26]

Вау!! 😲 Ты еще не читал? Это зря!

• Логика первого порядка
• Дизъюнктивная нормальная форма
• Конъюнктивная нормальная форма
• логика высказываний (пропозициональная логика )

Если я не полностью рассказал про пропозициональная логика? Напиши в комментариях Надеюсь, что теперь ты понял что такое пропозициональная логика, язык логики высказываний , логика высказываний , символическая логика и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Модели представления знаний