Привет, сегодня поговорим про вывод в логических моделях метод резолюций, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
вывод в логических моделях метод резолюций , настоятельно рекомендую прочитать все из категории Модели представления знаний.
Вывод в формальной логической системе является процедурой, которая из заданной группы выражений выводит отличное от заданных семантически правильное выражение. Эта процедура, представленная в определенной форме, и является правилом вывода. Если группа выражений, образующая посылку, является истинной, то должно гарантироваться, что применение правила вывода обеспечит получение истинного выражения в качестве заключения.
Наиболее часто используются два метода. Первый – метод правил вывода или метод естественного (натурального) вывода, названный так потому, что используемый тип рассуждений в исчислении предикатов приближается к обычному человеческому рассуждению. Второй – метод резолюций. В его основе лежит исчисление резольвент.
В этой статье рассматривается второй метод. Метод резолюций предложен в 1930г. в докторской диссертации Эрбрана для доказательства теорем в формальных системах первого порядка.
Метод резолюций опирается на исчисление резольвент. Существует теорема, утверждающая, что вопрос о доказуемости произвольной формулы в исчислении предикатов сводится к вопросу о доказуемости пустого списка в исчислении резольвент. Поэтому доказательство того, что список формул в исчислении резольвент пуст, эквивалентно доказательству ложности формулы в исчислении предикатов.
Идея метода резолюций заключается в том, что доказательство истинности или ложности выдвинутого предположения, например:
ведется методом от противного. Для этого в исходное множество предложений включают аксиомы формальной системы и отрицание доказываемой гипотезы:
Если в процессе доказательства возникает противоречие между отрицанием гипотезы и аксиомами, выражающееся в нахождении пустого списка (дизъюнкта), то выдвинутая гипотеза правильна.
Такое доказательство может быть получено на основании теоремы Эрбрана, гарантирующей, что существующее противоречие может быть всегда достигнуто за конечное число шагов, каковы бы ни были значения истинности, даваемые функциям, присутствующим в гипотезах и заключениях.
В методе резолюций множество предложений обычно рассматривается как составной предикат, содержащий несколько предикатов, соединенных логическими функциями и кванторами существования и общности. Так как одинаковые по смыслу предикаты могут иметь разный вид, то предложения преобразуются в клаузальную форму – разновидность конъюнктивной нормальной формы (КНФ), в которой удалены кванторы существования, всеобщности, символы импликации, равнозначности и др. Клаузальную форму называют сколемовской конъюнктивной формой.
В клаузальной форме вся исходная логическая формула представляется в виде множества предложений (клауз)

, называемых
клаузальным множеством 
:
Любое предложение

, из которого образуется клаузальное множество

, является совокупностью атомарных предикатов или их отрицаний, соединенных символом дизъюнкции:
Предикат или его отрицание называется дизъюнктом, литералом, атомом, атомарной формулой.
Сущность метода резолюций состоит в проверке, содержит или не содержит

пустое предложение
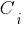
. Об этом говорит сайт https://intellect.icu . Предложение
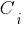
является пустым, если не содержит никаких литер. Так как условием истинности

является истинность всех
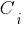
, входящих в

, то ложность какого-либо
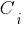
, заключающаяся в том, что множество
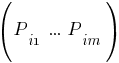
, образующее
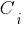
, окажется пустым, указывает на ложность исходной логической формулы.
Если

содержит пустое предложение
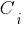
, то

противоречиво (невыполнимо). Если предложение
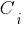
не является пустым, то делается попытка вывода предложений

пока не будет получено пустое (что всегда будет иметь место для невыполнимого

).
Для этого в двух предложениях, одно из которых состоит из одной литеры, а второе содержит произвольное число литер, находится
контрарная пара литер (например
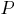
и
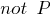
), которая вычеркивается, а из оставшихся частей формируется новое предложение (например из
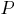
и
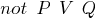
выводится
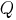
).
Предложение

, вновь сформированное из имеющихся
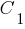
и

, называется
резольвентой 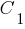
и

. Например:
Если при выводе предложений получены два однолитерных дизъюнкта, образующих контрарную пару, то их резольвентой будет пустой дизъюнкт. Так как наличие пустого дизъюнкта означает, что

является ложным, то невыполнимость исходного утверждения, сформулированного в виде отрицания:
доказывает истинность выдвинутого предположения:
Поскольку в логике предикатов в предложениях допускается наличие переменных, то для нахождения контрарных пар требуется введение операции унификации (подстановки константы вместо переменной в предикаты, имеющие одинаковые предикатные символы, но разные литеры). Алгоритм унификации разработали в 1966 г. Ж. Питра и независимо от него – Дж. Робинсон: чтобы унифицировать два различных выражения, отыскивается наиболее общий унификатор – НОУ (подстановка, при которой выражение с большей описательной мощностью согласуется с выражением, имеющим малую описательную мощность). Наличие этого алгоритма позволило реализовать метод резолюций Эрбрана в виде программы для ЭВМ.
Итак, если требуется методом резолюций доказать истинность какого-либо логического утверждения, то отрицание этого утверждения преобразуется в клаузальную форму, по его предложениям выполняется поиск пустого предложения с использованием унификации и вывода резольвент. Невыполнимость отрицания подтверждает истинность рассматриваемого утверждения.
Метод резолюций получил широкое распространение из-за высокой эффективности машинной обработки. На его основе построен язык «Prolog». Однако человек в процессе рассуждений такой логикой не пользуется, и это дает основание для поиска более естественных для человеческого сознания процедур вывода заключений.
Существенным недостатком метода резолюций является то, что он предназначен только для доказательства теорем. Он не пригоден для порождения новых предложений. К тому же, если предложение не является теоремой, резолюция может привести к построению бесконечного дерева решений.
Пример: вывод решения в логической модели на основе метода резолюций.
Даны утверждения:
- «Сократ – человек»;
- «Человек – это живое существо»;
- «Все живые существа смертны».
Требуется методом резолюций доказать утверждение «Сократ смертен».
Решение:
Шаг 1. Преобразуем высказывания в дизъюнктивную форму:
Шаг 2. Запишем отрицание целевого выражения (требуемого вывода), т.е. «Сократ бессмертен»:
Шаг 3. Cоставим конъюнкцию всех дизъюнктов (т. е. построим КНФ), включив в нее отрицание целевого выражения:
Шаг 4. В цикле проведем операцию поиска резольвент над каждой парой дизъюнктов:
Получение пустого дизъюнкта означает, что высказывание «Сократ бессмертен» ложно, значит истинно высказывание «Сократ смертен».
В целом метод резолюций интересен благодаря простоте и системности, но применим только для ограниченного числа случаев (доказательство не должно иметь большую глубину, а число потенциальных резолюций не должно быть большим). Кроме метода резолюций и правил вывода существуют другие методы получения выводов в логике предикатов.
К сожалению, в одной статье не просто дать все знания про вывод в логических моделях метод резолюций. Но я - старался.
Если ты проявишь интерес к раскрытию подробностей,я обязательно напишу продолжение! Надеюсь, что теперь ты понял что такое вывод в логических моделях метод резолюций
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Модели представления знаний
Из статьи мы узнали кратко, но содержательно про вывод в логических моделях метод резолюций
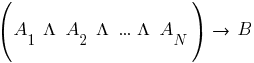

 , называемых клаузальным множеством
, называемых клаузальным множеством  :
:
 , из которого образуется клаузальное множество
, из которого образуется клаузальное множество  , является совокупностью атомарных предикатов или их отрицаний, соединенных символом дизъюнкции:
, является совокупностью атомарных предикатов или их отрицаний, соединенных символом дизъюнкции: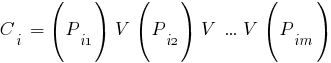
 пустое предложение
пустое предложение 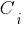 . Об этом говорит сайт https://intellect.icu . Предложение
. Об этом говорит сайт https://intellect.icu . Предложение 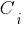 является пустым, если не содержит никаких литер. Так как условием истинности
является пустым, если не содержит никаких литер. Так как условием истинности  является истинность всех
является истинность всех 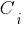 , входящих в
, входящих в  , то ложность какого-либо
, то ложность какого-либо 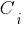 , заключающаяся в том, что множество
, заключающаяся в том, что множество 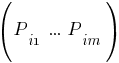 , образующее
, образующее 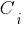 , окажется пустым, указывает на ложность исходной логической формулы.
, окажется пустым, указывает на ложность исходной логической формулы. содержит пустое предложение
содержит пустое предложение 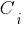 , то
, то  противоречиво (невыполнимо). Если предложение
противоречиво (невыполнимо). Если предложение 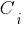 не является пустым, то делается попытка вывода предложений
не является пустым, то делается попытка вывода предложений  пока не будет получено пустое (что всегда будет иметь место для невыполнимого
пока не будет получено пустое (что всегда будет иметь место для невыполнимого  ).
).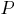 и
и 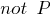 ), которая вычеркивается, а из оставшихся частей формируется новое предложение (например из
), которая вычеркивается, а из оставшихся частей формируется новое предложение (например из 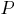 и
и 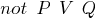 выводится
выводится 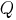 ).
). , вновь сформированное из имеющихся
, вновь сформированное из имеющихся 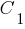 и
и  , называется резольвентой
, называется резольвентой 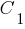 и
и  . Например:
. Например:


 является ложным, то невыполнимость исходного утверждения, сформулированного в виде отрицания:
является ложным, то невыполнимость исходного утверждения, сформулированного в виде отрицания:
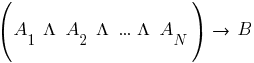


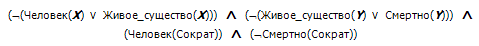

Комментарии
Оставить комментарий
Модели представления знаний
Термины: Модели представления знаний