Лекция
Привет, сегодня поговорим про минимальное остовное дерево, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое минимальное остовное дерево, алгоритм прима, остовное дерево, алгоритм краскала, алгоритм крускала, алгоритм борувки , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика..
минимальное остовное дерево (или минимальное покрывающее дерево) в связанном взвешенном неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него ребер.
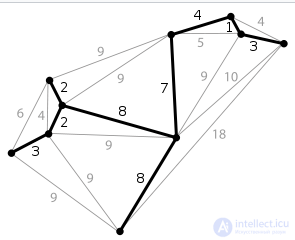
Пример минимального остовного дерева в графе. Числа на ребрах обозначают вес ребер.
Задача о нахождении минимального остовного дерева часто встречается в подобной постановке: допустим, есть nгородов, которые необходимо соединить дорогами, так, чтобы можно было добраться из любого города в любой другой (напрямую или через другие города). Разрешается строить дороги между заданными парами городов и известна стоимость строительства каждой такой дороги. Требуется решить, какие именно дороги нужно строить, чтобы минимизировать общую стоимость строительства.
Эта задача может быть сформулирована в терминах теории графов как задача о нахождении минимального остовного дерева в графе, вершины которого представляют города, ребра — это пары городов, между которыми можно проложить прямую дорогу, а вес ребра равен стоимости строительства соответствующей дороги.
Существует несколько алгоритмов для нахождения минимального остовного дерева. Некоторые наиболее известные из них перечислены ниже:
На задачу о нахождении минимального остовного дерева похожа задача о дереве Штейнера. В ней задано несколько точек на плоскости и требуется проложить между ними граф путей, так, чтобы минимизировать сумму длин путей. Главное отличие от задачи о минимальном остовном дереве при этом заключается в том, что разрешается добавлять дополнительные точки ветвления с целью еще сильнее уменьшить сумму длин ребер. Задача о дереве Штейнера является NP-полной.
При изучении сетей возникает задача построения минимального остовного дерева, т.е. задача соединения всех узлов сети с помощью путей наименьшей длины. Примером такой задачи является проектирование сети дорог, соединяющих населенные пункты, где дороги, соединяющие два пункта, могут проходить через другие населенные пункты. Наиболее экономичный проект должен минимизировать общую длину дорог.
Рассмотрим процедуру построения минимального остовного дерева. Обозначим:
X={ x1, x2, …, xn } - множество узлов сети;
Ck - связное множество узлов сети, соединенных алгоритмом после выполнения k-й итерации.
- множество узлов сети, не соединенных с узлами множества Ck после выполнения k-й итерации.
1. Об этом говорит сайт https://intellect.icu . Выбрать произвольный узел сети xi, C1={xi},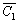 
= X\{xi}.
2. Выбрать из оставшихся узлов узел xj, ближайший к множеству узлов C1, C2={ xi, xj },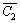 
= X\{ xi, xj }.
3. Выбрать из множества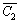 
узел, ближайший к узлам множества C2 , включить его в множество C2 и исключить из множества 
.
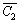За конечное число шагов будут обработаны все узлы сети и построено минимальное остовное дерево. Cn=X, 
=f.
Пример 1. Интернет компания планирует подключение к оптоволоконной сети пяти новых районов. Структура планируемой сети и расстояния между пунктами заданы рисунком-графом.
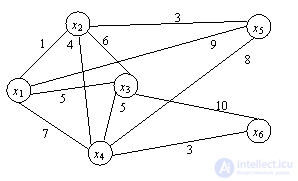
Требуется спроектировать наиболее экономичную оптоволоконную сеть.
Выполним пошаговое построение минимального остовного дерева для данной сети.
C0=f,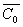 
=X={ x1, x2, x3, x4, x5, x6 }. Начнем с узла x1.
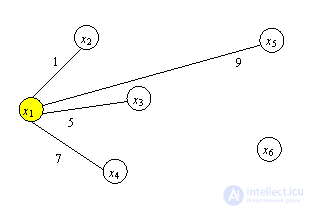
Итерация 1. C1={ x1 },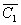 
={ x2, x3, x4, x5, x6 }, min (1,5,7,9)=1.
Ближайшим узлом к множеству C1 является x2. Добавляем его к остовному дереву с ребром длиной 1 км.
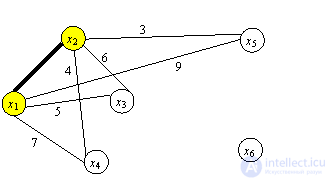
Итерация 2. C2={x1, x2},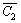 
={x3, x4, x5, x6}, min (3,4,5,6,7,9)=3.
Ближайшим узлом к множеству C2 является x5. Добавляем его к остовному дереву с ребром длиной 3 км.
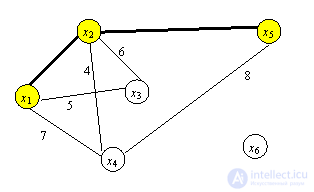
Итерация 3. C3={x1, x2, x5},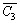 
={x3, x4, x6}, min (4,5,6,7,8)=4.
Ближайшим узлом к множеству C3 является x4. Добавляем его к остовному дереву с ребром длиной 4 км.
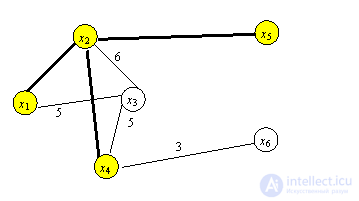
Итерация 4. C4={x1, x2, x4, x5},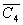 
={x3, x6}, min (3,5,6)=3.
Ближайшим узлом к множеству C4 является x6. Добавляем его к остовному дереву с ребром длиной 3 км.
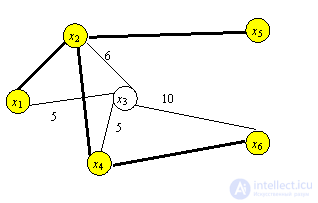
Итерация 5. C5={x1, x2, x4, x5, x6},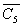 
={ x3 }, min (5,6,10)=5.
Ближайшим узлом к множеству C5 является x3.
Добавляем его к остовному дереву с ребром длиной 5 км.
При этом возможно два альтернативных соединения ( x1, x3 ) и ( x4, x3 ) длиной 5 км.
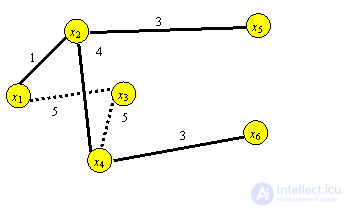
Процесс построения минимального остовного дерева завершен.
C6=X={x1, x2, x3, x4, x5, x6},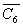 
=f.
Минимальная длина оптоволоконного кабеля составит 1+3+4+5+3=16 км.
|
Алгоритмы поиска на графах
|
|
|---|---|
| Неинформированные методы |
|
| Информированные методы |
|
| Кратчайшие пути |
|
| Минимальное остовное дерево |
|
| Другое |
|
Надеюсь, эта статья про минимальное остовное дерево, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое минимальное остовное дерево, алгоритм прима, остовное дерево, алгоритм краскала, алгоритм крускала, алгоритм борувки и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Из статьи мы узнали кратко, но содержательно про минимальное остовное дерево
Комментарии
Оставить комментарий
Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Термины: Дискретная математика. Теория множеств . Теория графов . Комбинаторика.