Лекция
Привет, сегодня поговорим про алгоритм беллмана-форда, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое алгоритм беллмана-форда, алгоритм беллмана , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
алгоритм беллмана - Форда позволяет решить задачу о кратчайшем пути из одной вершины в общем случае, когда вес каждого из ребер может быть отрицательным. Для заданного взвешенного ориентированного графа G = (V, Е) с истоком s и весовой функцией w : Е —» R алгоритм Беллмана -Форда возвращает логическое значение, указывающее на то, содержится ли в графе цикл с отрицательным весом, достижимый из истока . Если такой цикл существует, в алгоритме указывается, что решения не существует. Если же таких циклов нет, алгоритм выдает кратчайшие пути и их вес.
История алгоритма связана сразу с тремя независимыми математиками: Лестером Фордом, Ричардом Беллманом и Эдвардом Муром. Форд и Беллман опубликовали алгоритм в 1956 и 1958 годах соответственно, а Мур сделал это в 1957 году. И иногда его называют алгоритмом Беллмана – Форда – Мура. Метод используется в некоторых протоколах дистанционно-векторной маршрутизации, например в RIP (Routing Information Protocol – Протокол маршрутной информации).
Также как и алгоритм Дейкстры, алгоритм Беллмана — Форда вычисляет во взвешенном графе кратчайшие пути от одной вершины до всех остальных. Он подходит для работы с графами, имеющими ребра с отрицательным весом. Но спектр применимости алгоритма затрагивает не все такие графы, ввиду того, что каждый очередной проход по пути, составленному из ребер, сумма весов которых отрицательна (т. е. по отрицательному циклу), лишь улучшает требуемое значение. Бесконечное число улучшений делает невозможным определение одного конкретного значения, являющегося оптимальным. В связи с этим алгоритм Беллмана — Форда не применим к графам, имеющим отрицательные циклы, но он позволяет определить наличие таковых, о чем будет сказано позже.
Решить задачу, т. е. найти все кратчайшие пути из вершины s до всех остальных, используя алгоритм Беллмана — Форда, это значит воспользоваться методом динамического программирования: разбить ее на типовые подзадачи, найти решение последним, покончив тем самым с основной задачей. Здесь решением каждой из таких подзадач является определение наилучшего пути от одного отдельно взятого ребра, до какого-либо другого. Для хранения результатов работы алгоритма заведем одномерный массив d[]. В каждом его i-ом элементе будет храниться значение кратчайшего пути из вершины s до вершины i (если таковое имеется). Изначально, присвоим элементам массива d[] значения равные условной бесконечности (например, число заведомо большее суммы всех весов), а в элемент d[s] запишем нуль. Так мы задействовали известную и необходимую информацию, а именно известно, что наилучший путь из вершины s в нее же саму равен 0, и необходимо предположить недоступность других вершин из s. По мере выполнения алгоритма, для некоторых из них, это условие окажется ложным, и вычисляться оптимальные стоимости путей до этих вершин из s.
Задан граф G=(V, E), n=|V|, а m=|E|. Обозначим смежные вершины этого графа символами v и u (vÎV и uÎV), а вес ребра (v, u) символом w. Иначе говоря, вес ребра, выходящего из вершины v и входящего в вершину u, будет равен w. Тогда ключевая часть алгоритма Беллмана — Форда примет следующий вид:
Для i от 1 до n-1 выполнять
Для j от 1 до m выполнять
Если d[v] + w(v, u) < d[u] то
d[u] < d[v] + w(v, u)
На каждом n-ом шаге осуществляются попытки улучшить значения элементов массива d[]: если сумма, составленная из веса ребра w(v, u) и веса хранящегося в элементе d[v], меньше веса d[u], то она присваивается последнему.
#include "stdafx.h" #include #define inf 100000 using namespace std; struct Edges{ int u, v, w; }; const int Vmax=1000; const int Emax=Vmax*(Vmax-1)/2; int i, j, n, e, start; Edges edge[Emax]; int d[Vmax]; // алгоритм беллмана-форда void bellman_ford(int n, int s) { int i, j; for (i=0; id[s]=0; for (i=0; ifor (j=0; jif (d[edge[j].v]+edge[j].wd[edge[j].u]=d[edge[j].v]+edge[j].w; for (i=0; icout<"//главная функция void main() { setlocale(LC_ALL, "Rus"); int w; cout<<"Количество вершин > "; cin>>n; e=0; for (i=0; ifor (j=0; j{ cout<<"Вес "<"< "; cin>>w; if (w!=0) { edge[e].v=i; edge[e].u=j; edge[e].w=w; e++; } } cout<<"Стартовая вершина > "; cin>>start; cout<<"Список кратчайших путей:"; bellman_ford(n, start-1); system("pause>>void"); }
program Ford_Bellman; uses crt; const inf=100000; Vmax=1000; Emax=Vmax*(Vmax-1) div 2; type Edges=record u, v, w: integer; end; Var i, j, e, n, w, start: integer; edge: array[1..Emax] of Edges; d: array[1..Vmax] of integer; {алгоритм Беллмана-Форда} procedure FB(n, s: integer); begin for i:=1 to n do d[i]:=inf; d[s]:=0; for i:=1 to n-1 do for j:=1 to e-1 do if d[edge[j].v]+edge[j].wd[edge[j].u]:=d[edge[j].v]+edge[j].w; for i:=1 to n do if d[i]=inf then writeln(start, '->', i, '=', 'Not') else writeln(start, '->', i, '=', d[i]); end; {основной блок программы} begin clrscr; write('Количество вершин > '); read(n); e:=1; for i:=1 to n do for j:=1 to n do begin write('Вес ', i, '->', j, ' > '); read(w); if w<>0 then begin edge[e].v:=i; edge[e].u:=j; edge[e].w:=w; e:=e+1; end; end; write('Стартовая вершина > '); read(start); writeln('Список кратчайших путей:'); FB(n, start); end.
Здесь граф представлен упрощенным списком ребер, который формируется по мере ввода пользователем матрицы весов. Об этом говорит сайт https://intellect.icu . Основная часть алгоритма Беллмана – Форда (проверка условия) выполняется m*(n-1) раз, т. к. число повторений внешнего цикла равно n-1, а внутреннего – m. Отказ от n-ой итерации целесообразен, поскольку алгоритм справляется со своей задачей за n-1 шаг, но запуск внешнего цикла n раз позволит выявить наличие отрицательного цикла в графе. Проверить это можно, например, при помощи следующей модификации:
|
bool x=true;
for (i=0; i{ if (i!=n-1) for (j=0; jif (d[edge[j].v]+edge[j].wd[edge[j].u]=d[edge[j].v]+edge[j].w; if (i==n-1) for (j=0; jif (d[edge[j].v]+edge[j].w} if (!x) cout< |
Здесь внешний цикл выполняется n раз (в C++ принято начальным указывать значение 0, поэтому для данного кода n-1 раз), и если на n-ой стадии будет возможно улучшение, то это свидетельствует о наличие отрицательного цикла.
В этом алгоритме используется ослабление, в результате которого величина d[v], представляющая собой оценку веса кратчайшего пути из истока s к каждой из вершин v є V, уменьшается до тех пор, пока она не станет равна фактическому весу кратчайшего пути из s в v. Значение TRUE возвращается алгоритмом тогда и только тогда, когда граф не содержит циклов с отрицательным весом, достижимых из истока.
Bellman_Ford(G, w, s) 1 Initialize_Single_Source(G, s) 2 for i «- l to |V[G]|-1 3 do for (для) каждого ребра (u, v) є E[G] 4 do RELAX(u,v,w) 5 for (для) каждого ребра (u, v) є E[G] 6 do if d[v] > d[u] + w(u, v) 7 then return FALSE 8 return TRUE
После инициализации в строке 1 всех значений d и prev, алгоритм осуществляет |V| — 1 проходов по ребрам графа. Каждый проход соответствует одной итерации цикла for в строках 2-4 и состоит из однократного ослабления каждого ребра графа. После |V| — 1 проходов в строках 5-8 проверяется наличие цикла с отрицательным весом и возвращается соответству- ющее булево значение.
Алгоритм Беллмана-Форда завершает свою работу в течение времени O(V*E), поскольку инициализация в строке 1 занимает время O(V), на каждый из |V| — 1 проходов по ребрам в строках 2-4 требуется время в O(E), а на выполнение цикла for в строках 5-7 — время O(Е).
Давайте разберемся в алгоритме на следующем примере графа. Изображения взяты отсюда.
Пусть начальная вершина равна 0. Примите все расстояния за бесконечные, кроме расстояния до самой src. Общее число вершин в графе равно 5, поэтому все ребра нужно пройти 4 раза.
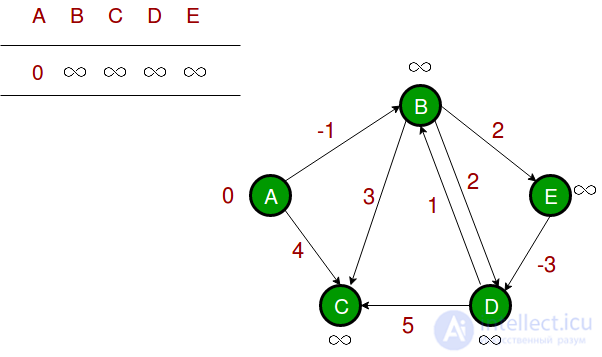
Пусть ребра отрабатываются в следующем порядке: (B, E), (D, B), (B, D), (A, B), (A, C), (D, C), (B, C), (E, D). Мы получаем следующие расстояния, когда проход по ребрам был совершен первый раз. Первая строка показывает начальные расстояния, вторая строка показывает расстояния, когда ребра (B, E), (D, B), (B, D) и (A, B) обрабатываются. Третья строка показывает расстояние при обработке (A, C). Четвертая строка показывает, что происходит, когда обрабатываются (D, C), (B, C) и (E, D).
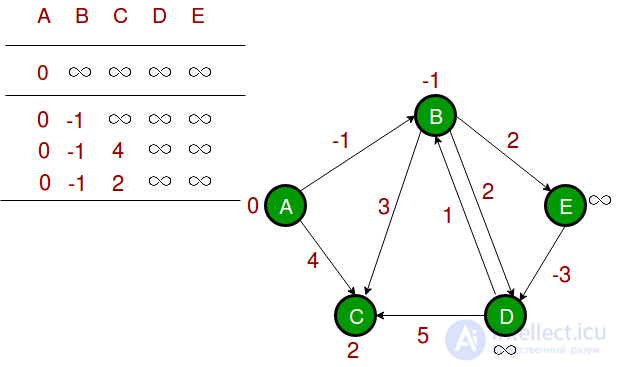
Первая итерация гарантирует, что все самые короткие пути будут не длиннее пути в 1 ребро. Мы получаем следующие расстояния, когда будет совершен второй проход по всем ребрам (в последней строке показаны конечные значения).
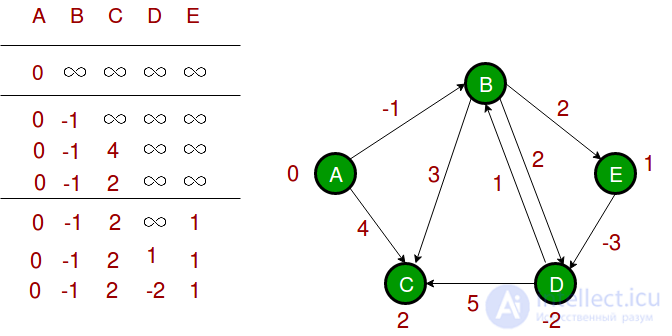
Вторая итерация гарантирует, что все кратчайшие пути будут иметь длину не более 2 ребер. Алгоритм проходит по всем ребрам еще 2 раза. Расстояния минимизируются после второй итерации, поэтому третья и четвертая итерации не обновляют значения расстояний.
Алгоритм Беллмана-Форда позволяет очень просто определить, существует ли в графе отрицательный цикл, достижимый из вершины
. Достаточно произвести внешнюю итерацию цикла не
, a ровно
раз. Если при исполнении последней итерации длина кратчайшего пути до какой-либо вершины строго уменьшилась, то в графе есть отрицательный цикл, достижимый из
. На основе этого можно предложить следующую оптимизацию: отслеживать изменения в графе и, как только они закончатся, сделать выход из цикла (дальнейшие итерации будут бессмысленны).
|
Алгоритмы поиска на графах
|
|
|---|---|
| Неинформированные методы |
|
| Информированные методы |
|
| Кратчайшие пути |
|
| Минимальное остовное дерево | |
| Другое |
|
На этом все! Теперь вы знаете все про алгоритм беллмана-форда, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое алгоритм беллмана-форда, алгоритм беллмана и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов