Лекция
Привет, сегодня поговорим про линейный поиск, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое линейный поиск , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
Линейный, последовательный поиск — алгоритм нахождения заданного значения произвольной функции на некотором отрезке. Данный алгоритм является простейшим алгоритмом поиска и, в отличие, например, от двоичного поиска, не накладывает никаких ограничений на функцию и имеет простейшую реализацию. Поиск значения функции осуществляется простым сравнением очередного рассматриваемого значения (как правило, поиск происходит слева направо, то есть от меньших значений аргумента к большим) и, если значения совпадают (с той или иной точностью), то поиск считается завершенным.
Если отрезок имеет длину N, то найти решение с точностью до 
можно за время 
. Т.о. асимптотическая сложность алгоритма — 
. В связи с малой эффективностью по сравнению с другими алгоритмами
линейный поиск обычно используют, только если отрезок поиска содержит очень мало элементов, тем не менее, линейный поиск не требует дополнительной памяти или обработки/анализа функции, так что может работать в потоковом режиме при непосредственном получении данных из любого источника. Также линейный поиск часто используется в виде линейных алгоритмов поиска максимума/минимума.
Переменные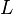 
и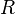 
содержат, соответственно, левую и правую границы отрезка массива, где находится нужный нам элемент. Исследования начинаются с первого элемента отрезка. Если искомое значение не равно значению функции в данной точке, то осуществляется переход к следующей точке. То есть, в результате каждой проверки область поиска уменьшается на один элемент.
int function LinearSearch (Array A, int L, int R, int Key);
begin
for X = L to R do
if A[X] = Key then
return X
return -1; // элемент не найден
end;
В качестве примера можно рассмотреть поиск значения функции на множестве целых чисел, представленной таблично.
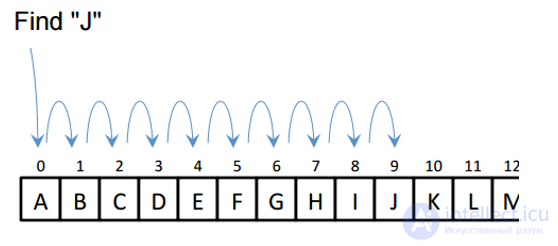
Для нахождения некоторого элемента (ключа) в заданном неупорядоченном массиве используется алгоритм линейного (последовательного) поиска. Он работает как с неотсортированными массивами, так и отсортированными, но для вторых существуют алгоритмы эффективнее линейного поиска. Эту неэффективность компенсируют простая реализация алгоритма и сама возможность применять его к неупорядоченным последовательностям. Об этом говорит сайт https://intellect.icu . Здесь, а также при рассмотрении всех других алгоритмов поиска, будем полагать, что в качестве ключа выступает некоторая величина, по мере выполнения алгоритма, сравниваемая именно со значениями элементов массива.
Слово «последовательный» содержит в себе основную идею метода. Начиная с первого, все элементы массива последовательно просматриваются и сравниваются с искомым. Если на каком-то шаге текущий элемент окажется равным искомому, тогда элемент считается найденным, и в качестве результата возвращается номер этого элемента, либо другая информация о нем. (Далее, в качестве выходных данных будет выступать номер элемента). Иначе, следуют возвратить что-то, что может оповестить о его отсутствии в пройденной последовательности.
Ниже, на примере фигур, наглядно демонстрируется работа алгоритма линейного поиска. В качестве искомого элемента (в данном случае это квадрат) задается фигура, и она поочередно сравнивается со всеми имеющимися фигурами до тех пор, пока не будет найдена тождественная ей фигура, или окажется, что в данном множестве таковой нет.
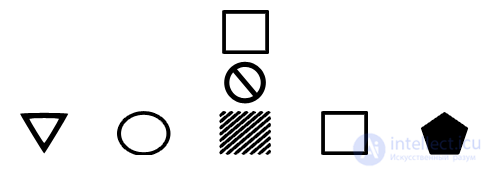
Примечателен тот факт, что имеется вероятность наличия нескольких элементов с одинаковыми значениями, совпадающими со значением ключа. В таком случае, если нет конкретных условий, можно, например, за результирующий взять номер первого найденного элемента (реализовано в листинге ниже), или записать в массив номера всех тождественных элементов.
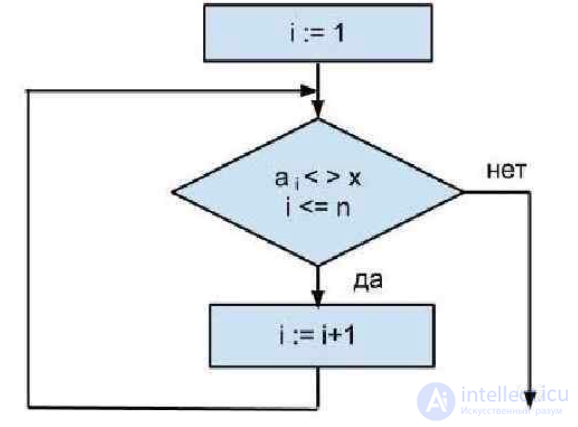
Рис 1. блок-схема алгоритма линейного поиска
где a1, a2, a3, … , an – задан массив из n элементов;
X – это эталон который необходимо найти;
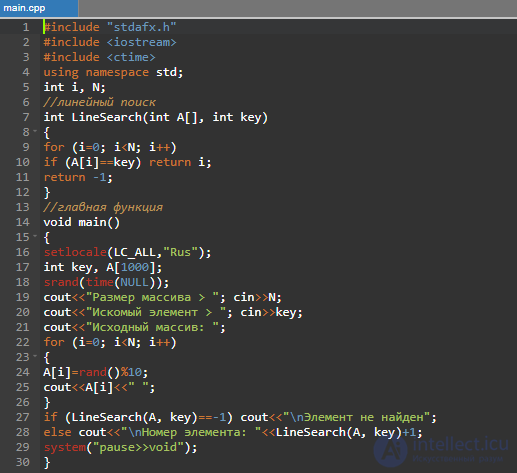
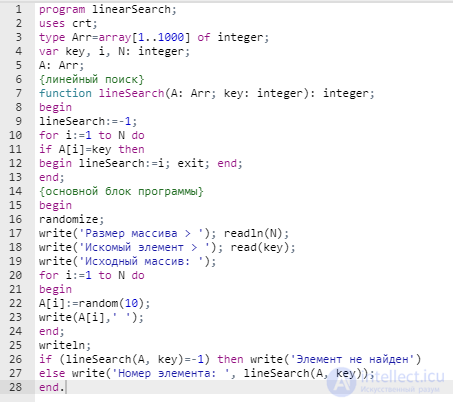
Переменные 
и 
содержат, соответственно, левую и правую границы отрезка массива, где находится нужный нам элемент. Исследования начинаются с первого элемента отрезка. Если искомое значение не равно значению функции в данной точке, то осуществляется переход к следующей точке. То есть в результате каждой проверки область поиска уменьшается на один элемент.
Пример на Swift 3, с "ускоренным" поиском:
Пример линеного поиска на языке PHP
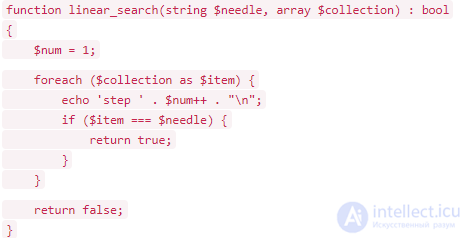
В лучшем случае, когда искомый элемент занимает первую позицию, алгоритм произведет всего одно сравнение, а в худшем N, где N — количество элементов в массиве. Худшему случаю соответствуют две ситуации: искомый элемент занимает последнюю позицию, или он вовсе отсутствует в массиве.
Алгоритм линейного поиска не часто используется на практике, поскольку принцип работы «в лоб» делает скорость решения им задачи очень низкой. Его применение оправдано на небольших и/или неотсортированных последовательностях, но когда последовательность состоит из большого числа элементов, и с ней предстоит работать не раз, тогда наиболее оптимальным решением оказывается предварительная сортировка этой последовательности с последующим применением двоичного или другого, отличного от линейного, алгоритма поиска.
Для списка из n элементов лучшим случаем будет тот, при котором искомое значение равно первому элементу списка и требуется только одно сравнение. Худший случай будет тогда, когда значения в списке нет (или оно находится в самом конце списка), в случае чего необходимо n сравнений.
Если искомое значение входит в список k раз и все вхождения равновероятны, то ожидаемое число сравнений
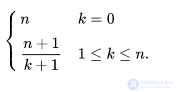
Например, если искомое значение встречается в списке один раз, и все вхождения равновероятны, то среднее число сравнений равно 
. Однако, если известно, что оно встречается один раз, то достаточно n — 1 сравнений, и среднее число сравнений будет равняться
(для n = 2 это число равняется 1, что соответствует одной конструкции if-then-else).
В любом случае вычислительная сложность алгоритма O(n).
Если предположить, что количество элементов в структуре 1 млн или более, то сложно назвать алгоритм “линейный поиск” подходящим, так как его эффективность маловероятно будет высокой. Поэтому в зависимости от задачи и ее условий может применяться свой наиболее рациональный для конкретного случая алгоритм. Например для поиска элемента в большом наборе данных можно применить алгоритм “двоичный поиск”.
Необходимо также отметить, что все ранее сказанное относительно эффективности применимо к структуре, в которой хранятся только уникальные значения. Но имена могут и повторяться, не правда ли? В структуре данных могут располагаться например два человека с именем Karl, тогда эффективность алгоритма линейный поиск сразу же падает. Почему? Потому что алгоритму уже необходимо произвести не N/2 шагов при поиске, а все N, так как найдя нужное значение цикл не должен прерываться и обязан дойти до конца.
При выборе подходящего алгоритма должны быть учтен такой важный момент как возможность или невозможность хранения дубликатов в структуре данных.
Обычно линейный поиск очень прост в реализации и применим, если список содержит мало элементов, либо в случае одиночного поиска в неупорядоченном списке.
Если предполагается поиск в одном и том же списке большое число раз, то часто имеет смысл предварительной обработки списка, например, сортировки и последующего использования бинарного поиска, либо построения какой-либо эффективной структуры данных для поиска. Частая модификация списка также может оказывать влияние на выбор дальнейших действий, поскольку делает необходимым процесс перестройки структуры.
На этом все! Теперь вы знаете все про линейный поиск, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое линейный поиск и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Из статьи мы узнали кратко, но содержательно про линейный поиск
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов