Длинная арифметика с примерами на Си кратко

Привет, Вы узнаете о том , что такое длинная арифметика, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое длинная арифметика , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

длинная арифметика — это набор программных средств (структуры данных и алгоритмы), которые позволяют работать с числами гораздо больших величин, чем это позволяют стандартные типы данных.

Виды целочисленной длинной арифметики

Вообще говоря, даже только в олимпиадных задачах набор средств достаточно велик, поэтому произведем классификацию различных видов длинной арифметики.

Классическая длинная арифметика

Основная идея заключается в том, что число хранится в виде массива его цифр.

Цифры могут использоваться из той или иной системы счисления, обычно применяются десятичная система счисления и ее степени (десять тысяч, миллиард), либо двоичная система счисления.

Операции над числами в этом виде длинной арифметики производятся с помощью "школьных" алгоритмов сложения, вычитания, умножения, деления столбиком. Впрочем, к ним также применимы алгоритмы быстрого умножения: Быстрое преобразование Фурье и Алгоритм Карацубы.

Здесь описана работа только с неотрицательными длинными числами. Для поддержки отрицательных чисел необходимо ввести и поддерживать дополнительный флаг "отрицательности" числа, либо же работать в дополняющих кодах.

Структура данных

Хранить длинные числа будем в виде вектора чисел 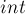, где каждый элемент — это одна цифра числа.

typedef vector<int> lnum;

Для повышения эффективности будем работать в системе по основанию миллиард, т.е. каждый элемент вектора 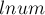содержит не одну, а сразу 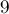цифр:

const int base = 1000*1000*1000;

Цифры будут храниться в векторе в таком порядке, что сначала идут наименее значимые цифры (т.е. единицы, десятки, сотни, и т.д.).

Кроме того, все операции будут реализованы таким образом, что после выполнения любой из них лидирующие нули (т.е. лишние нули в начале числа) отсутствуют (разумеется, в предположении, что перед каждой операцией лидирующие нули также отсутствуют). Следует отметить, что в представленной реализации для числа ноль корректно поддерживаются сразу два представления: пустой вектор цифр, и вектор цифр, содержащий единственный элемент — ноль.

Вывод

Самое простое — это вывод длинного числа.

Сначала мы просто выводим самый последний элемент вектора (или 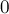, если вектор пустой), а затем выводим все оставшиеся элементы вектора, дополняя их нулями до 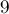символов:

printf ("%d", a.empty() ? 0 : a.back());
for (int i=(int)a.size()-2; i>=0; --i)
	printf ("%09d", a[i]);

(здесь небольшой тонкий момент: нужно не забыть записать приведение типа 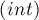, поскольку в противном случае число 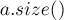будут беззнаковым, и если 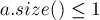, то при вычитании произойдет переполнение)

Чтение

Считываем строку в 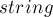, и затем преобразовываем ее в вектор:

for (int i=(int)s.length(); i>0; i-=9)
	if (i < 9)
		a.push_back (atoi (s.substr (0, i).c_str()));
	else
		a.push_back (atoi (s.substr (i-9, 9).c_str()));

Если использовать вместо 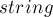массив 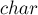'ов, то код получится еще компактнее:

for (int i=(int)strlen(s); i>0; i-=9) {
	s[i] = 0;
	a.push_back (atoi (i>=9 ? s+i-9 : s));
}

Если во входном числе уже могут быть лидирующие нули, то их после чтения можно удалить таким образом:

while (a.size() > 1 && a.back() == 0)
	a.pop_back();

Сложение

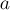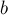Прибавляет к числу число и сохраняет результат в :

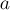int carry = 0;
for (size_t i=0; i(a.size(),b.size()) || carry; ++i) {
	if (i == a.size())
		a.push_back (0);
	a[i] += carry + (i < b.size() ? b[i] : 0);
	carry = a[i] >= base;
	if (carry)  a[i] -= base;
}

Вычитание

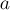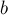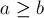Отнимает от числа число () и сохраняет результат в :

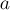int carry = 0;
for (size_t i=0; i() || carry; ++i) {
	a[i] -= carry + (i < b.size() ? b[i] : 0);
	carry = a[i] < 0;
	if (carry)  a[i] += base;
}
while (a.size() > 1 && a.back() == 0)
	a.pop_back();

Здесь мы после выполнения вычитания удаляем лидирующие нули, чтобы поддерживать предикат о том, что таковые отсутствуют.

Умножение длинного на короткое

Умножает длинное 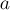на короткое 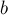(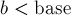) и сохраняет результат в :

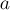int carry = 0;
for (size_t i=0; i() || carry; ++i) {
	if (i == a.size())
		a.push_back (0);
	long long cur = carry + a[i] * 1ll * b;
	a[i] = int (cur % base);
	carry = int (cur / base);
}
while (a.size() > 1 && a.back() == 0)
	a.pop_back();

Здесь мы после выполнения деления удаляем лидирующие нули, чтобы поддерживать предикат о том, что таковые отсутствуют.

(Примечание: способ дополнительной оптимизации. Об этом говорит сайт https://intellect.icu . Если скорость работы чрезвычайно важна, то можно попробовать заменить два деления одним: посчитать только целую часть от деления (в коде это переменная 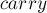), а затем уже посчитать по ней остаток от деления (с помощью одной операции умножения). Как правило, этот прием позволяет ускорить код, хотя и не очень значительно.)

Умножени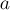е двух длинных чисел

Умножает на 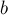и результат сохраняет в :

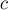lnum c (a.size()+b.size());
for (size_t i=0; i(); ++i)
	for (int j=0, carry=0; j<(int)b.size() || carry; ++j) {
		long long cur = c[i+j] + a[i] * 1ll * (j < (int)b.size() ? b[j] : 0) + carry;
		c[i+j] = int (cur % base);
		carry = int (cur / base);
	}
while (c.size() > 1 && c.back() == 0)
	c.pop_back();

Деление длинного на короткое

Делит длинное 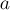на короткое 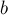(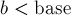), частное сохраняет в 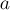, остаток в :

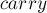int carry = 0;
for (int i=(int)a.size()-1; i>=0; --i) {
	long long cur = a[i] + carry * 1ll * base;
	a[i] = int (cur / b);
	carry = int (cur % b);
}
while (a.size() > 1 && a.back() == 0)
	a.pop_back();

Длинная арифметика в факторизованном виде

Здесь идея заключается в том, чтобы хранить не само число, а его факторизацию, т.е. степени каждого входящего в него простого.

Этот метод также весьма прост для реализации, и в нем очень легко производить операции умножения и деления, однако невозможно произвести сложение или вычитание. С другой стороны, этот метод значительно экономит память в сравнении с "классическим" подходом, и позволяет производить умножение и деление значительно (асимптотически) быстрее.

Этот метод часто применяется, когда необходимо производить деление по непростому модулю: тогда достаточно хранить число в виде степеней по простым делителям этого модуля, и еще одного числа — остатка по этому же модулю.

Длинная арифметика по системе простых модулей (Китайская теорема или схема Гарнера)

Суть в том, что выбирается некоторая система модулей (обычно небольших, помещающихся в стандартные типы данных), и число хранится в виде вектора из остатков от его деления на каждый из этих модулей.

Как утверждает Китайская теорема об остатках, этого достаточно, чтобы однозначно хранить любое число в диапазоне от 0 до произведения этих модулей минус один. При этом имеется Алгоритм Гарнера, который позволяет произвести это восстановление из модульного вида в обычную, "классическую", форму числа.

Таким образом, этот метод позволяет экономить память по сравнению с "классической" длинной арифметикой (хотя в некоторых случаях не столь радикально, как метод факторизации). Крому того, в модульном виде можно очень быстро производить сложения, вычитания и умножения, — все за асимптотически однаковое время, пропорциональное количеству модулей системы.

Однако все это дается ценой весьма трудоемкого перевода числа из этого модульного вида в обычный вид, для чего, помимо немалых временных затрат, потребуется также реализация "классической" длинной арифметики с умножением.

Помимо этого, производить деление чисел в таком представлении по системе простых модулей не представляется возможным.

Виды дробной длинной арифметики

Операции над дробными числами встречаются в олимпиадных задачах гораздо реже, и работать с огромными дробными числами значительно сложнее, поэтому в олимпиадах встречается только специфическое подмножество дробной длинной арифметики.

Длинная арифметика в несократимых дробях

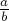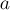Число представляется в виде несократимой дроби , где и 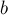— целые числа. Тогда все операции над дробными числами нетрудно свести к операциям над числителями и знаменателями этих дробей.

Обычно при этом для хранения числителя и знаменателя приходится также использовать длинную арифметику, но, впрочем, самый простой ее вид — "классическая" длинная арифметика, хотя иногда оказывается достаточно встроенного 64-битного числового типа.

Выделение позиции плавающей точки в отдельный тип

Иногда в задаче требуется производить расчеты с очень большими либо очень маленькими числами, но при этом не допускать их переполнения. Встроенный 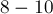-байтовый тип 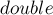, как известно, допускает значения экспоненты в диапазоне 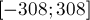, чего иногда может оказаться недостаточно.

Прием, собственно, очень простой — вводится еще одна целочисленная переменная, отвечающая за экспоненту, а после выполнения каждой операции дробное число "нормализуется", т.е. возвращается в отрезок 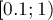, путем увеличения или уменьшения экспоненты.

При перемножении или делении двух таких чисел надо соответственно сложить либо вычесть их экспоненты. При сложении или вычитании перед выполнением этой операции числа следует привести к одной экспоненте, для чего одно из них домножается на 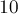в степени разности экспонент.

Наконец, понятно, что не обязательно выбирать 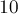в качестве основания экспоненты. Исходя из устройства встроенных типов с плавающей точкой, самым выгодным представляется класть основание равным .

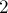Данная статья про длинная арифметика подтверждают значимость применения современных методик для изучения данных проблем. Надеюсь, что теперь ты понял что такое длинная арифметика и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов