Пирамидальная сортировка (Heapsort, Сортировка кучей)

Привет, Вы узнаете о том , что такое пирамидальная сортировка, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое пирамидальная сортировка, heapsort, сортировка кучей , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

Метод пирамидальной сортировки, изобретенный Д. Уилльямсом, является улучшением традиционных сортировок с помощью дерева.

Пирамидой (кучей) называется двоичное дерево такое, что

a[i] ≤ a[2i+1];

a[i] ≤ a[2i+2].

Подробнее

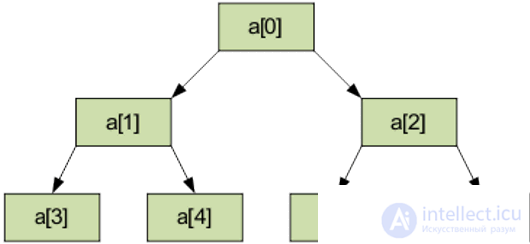
a — минимальный элемент пирамиды.

Общая идея пирамидальной сортировки заключается в том, что сначала строится пирамида из элементов исходного массива, а затем осуществляется сортировка элементов.

Выполнение алгоритма разбивается на два этапа.

1 этап Построение пирамиды. Определяем правую часть дерева, начиная с n/2-1 (нижний уровень дерева). Берем элемент левее этой части массива и просеиваем его сквозь пирамиду по пути, где находятся меньшие его элементы, которые одновременно поднимаются вверх; из двух возможных путей выбираете путь через меньший элемент.

Например, массив для сортировки

24, 31, 15, 20, 52, 6

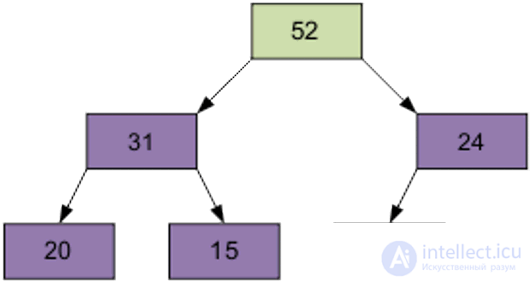
Расположим элементы в виде исходной пирамиды; номер элемента правой части (6/2-1)=2 — это элемент 15.


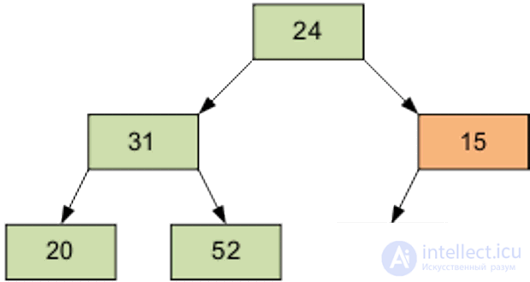
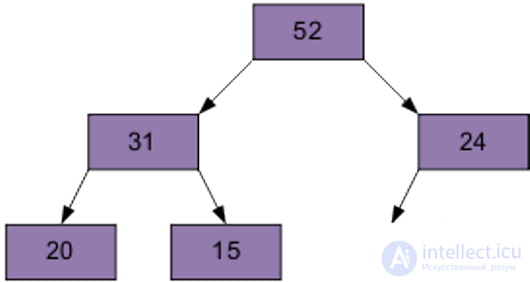
Результат просеивания элемента 15 через пирамиду.


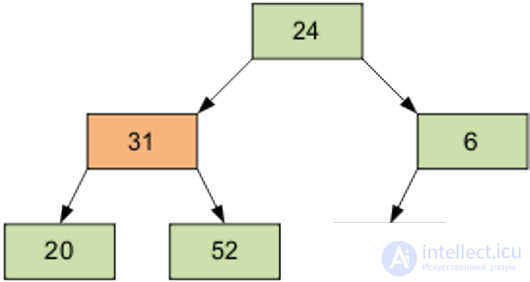
Следующий просеиваемый элемент – 1, равный 31.


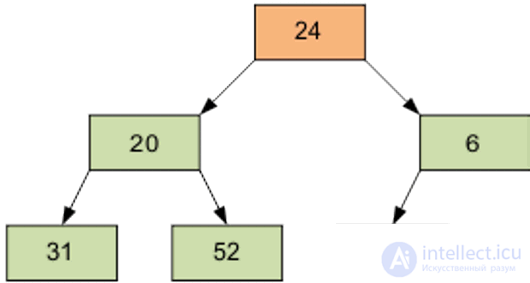
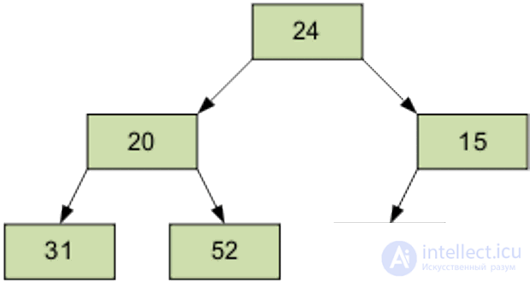
Затем – элемент 0, равный 24.


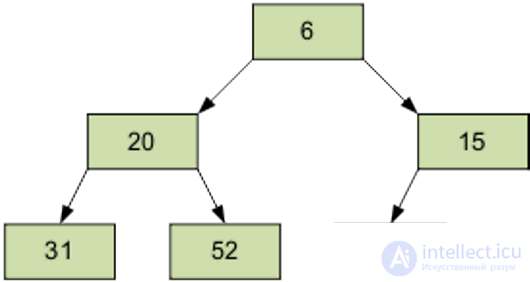
Разумеется, полученный массив еще не упорядочен. Однако процедура просеивания является основой для пирамидальной сортировки. В итоге просеивания наименьший элемент оказывается на вершине пирамиды.

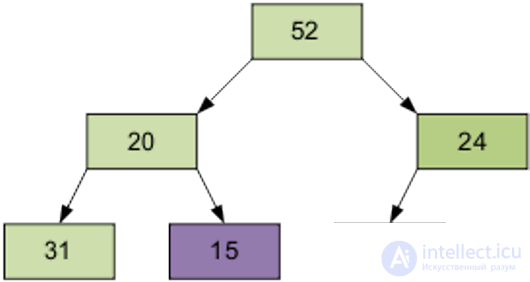
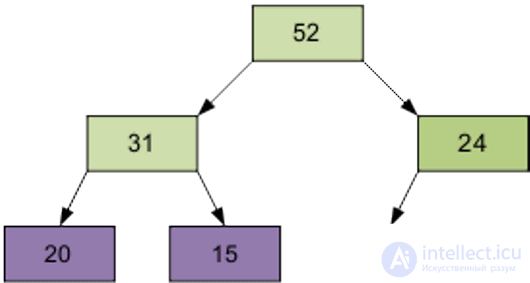
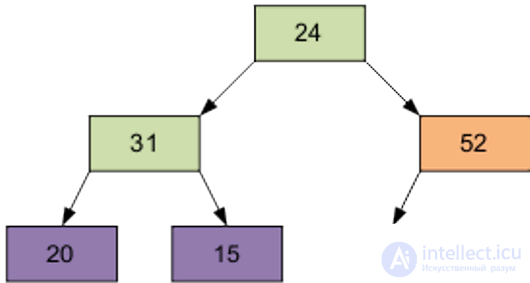
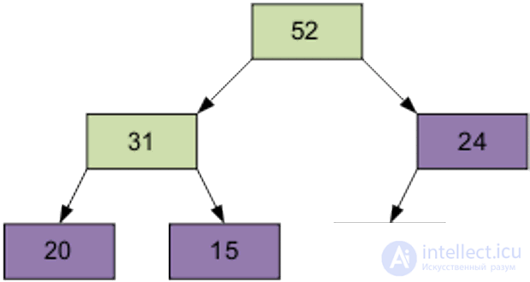
2 этап Сортировка на построенной пирамиде. Берем последний элемент массива в качестве текущего. Меняем верхний (наименьший) элемент массива и текущий местами. Об этом говорит сайт https://intellect.icu . Текущий элемент (он теперь верхний) просеиваем сквозь n-1 элементную пирамиду. Затем берем предпоследний элемент и т.д.




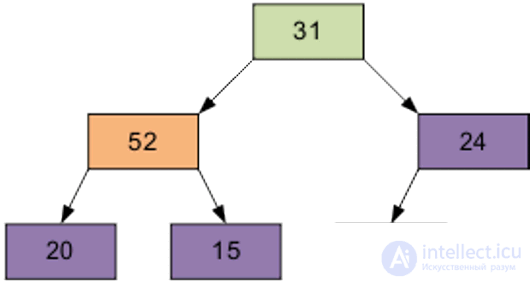
Продолжим процесс. В итоге массив будет отсортирован по убыванию.

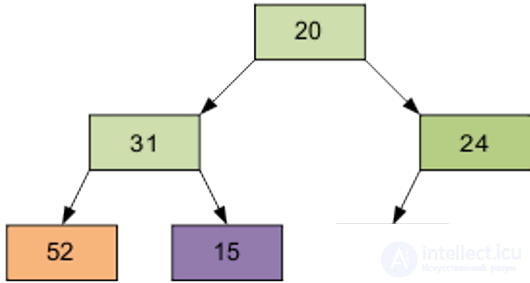
Реализация пирамидальной сортировки на Си

#include
#include
// Функция "просеивания" через кучу - формирование кучи
void siftDown(int *numbers, int root, int bottom)
{
int maxChild; // индекс максимального потомка
int done = 0; // флаг того, что куча сформирована
// Пока не дошли до последнего ряда
while ((root * 2 <= bottom) && (!done))
{
if (root * 2 == bottom) // если мы в последнем ряду,
maxChild = root * 2; // запоминаем левый потомок
// иначе запоминаем больший потомок из двух
else if (numbers[root * 2] > numbers[root * 2 + 1])
maxChild = root * 2;
else
maxChild = root * 2 + 1;
// если элемент вершины меньше максимального потомка
if (numbers[root] < numbers[maxChild])
{
int temp = numbers[root]; // меняем их местами
numbers[root] = numbers[maxChild];
numbers[maxChild] = temp;
root = maxChild;
}
else // иначе
done = 1; // пирамида сформирована
}
}
// Функция сортировки на куче
void heapSort(int *numbers, int array_size)
{
// Формируем нижний ряд пирамиды
for (int i = (array_size / 2) - 1; i >= 0; i--)
siftDown(numbers, i, array_size - 1);
// Просеиваем через пирамиду остальные элементы
for (int i = array_size - 1; i >= 1; i--)
{
int temp = numbers ;
numbers  = numbers[i];
numbers[i] = temp;
siftDown(numbers, 0, i - 1);
}
}
int main()
{
int a[10];
// Заполнение массива случайными числами
for (int i = 0; i<10; i++)
a[i] = rand() % 20 - 10;
// Вывод элементов массива до сортировки
for (int i = 0; i<10; i++)
printf("%d ", a[i]);
printf("\n");
heapSort(a, 10); // вызов функции сортировки
// Вывод элементов массива после сортировки
for (int i = 0; i<10; i++)
printf("%d ", a[i]);
printf("\n");
getchar();
return 0;
}

Результат выполнения

Анализ алгоритма пирамидальной сортировки

Несмотря на некоторую внешнюю сложность, пирамидальная сортировка является одной из самых эффективных. Алгоритм сортировки эффективен для больших n. В худшем случае требуется n·log2n шагов, сдвигающих элементы. Среднее число перемещений примерно равно

(n/2)·log2n,

и отклонения от этого значения относительно невелики.

Достоинства и недостатки

Достоинства

• Имеет доказанную оценку худшего случая O(n log n).
• Сортирует на месте, то есть требует всего O(1) дополнительной памяти (если дерево организовывать так, как показано выше).

Недостатки

• Неустойчив — для обеспечения устойчивости нужно расширять ключ.
• На почти отсортированных массивах работает столь же долго, как и на хаотических данных.
• На одном шаге выборку приходится делать хаотично по всей длине массива — поэтому алгоритм плохо сочетается с кэшированием и подкачкой памяти.
• Методу требуется «мгновенный» прямой доступ; не работает на связанных списках и других структурах памяти последовательного доступа.
• Не распараллеливается.

Сортировка слиянием при расходе памяти O(n) быстрее ( O(n log n). с меньшей константой) и не подвержена деградации на неудачных данных.

Из-за сложности алгоритма выигрыш получается только на больших n. На небольших n (до нескольких тысяч) быстрее сортировка Шелла.

Применение

Алгоритм « сортировка кучей » активно применяется в ядре Linux.

Анализ данных, представленных в статье про пирамидальная сортировка, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое пирамидальная сортировка, heapsort, сортировка кучей и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов