Динамическое программирование

Сразу хочу сказать, что здесь никакой воды про динамическое программирование, и только нужная информация. Для того чтобы лучше понимать что такое динамическое программирование , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

динамическое программирование в теории управления и теории вычислительных систем — способ решения сложных задач путем разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой, выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной. В этом случае время вычислений, по сравнению с «наивными» методами, можно значительно сократить.

Динамическое программирование - раздел математики , посвященный теории и методам решения многошаговых задач оптимального управления .

Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.

Метод динамического программирования сверху - это простое запоминание результатов решения тех подзадач, которые могут повторно встретиться в дальнейшем. Динамическое программирование снизу включает в себя переформулирование сложной задачи в виде рекурсивной последовательности более простых подзадач.

История

Словосочетание «динамическое программирование» впервые было использовано в 1940-х годах Р. Беллманом для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения задачи, «предшествующей» ей. В 1953 г. он уточнил это определение до современного. Первоначально эта область была основана, каксистемный анализ и инжиниринг, которая была признана IEEE. Вклад Беллмана в динамическое программирование был увековечен в названии уравнения Беллмана, центрального результата теории динамического программирования, который переформулирует оптимизационную задачу в рекурсивной форме.

Слово «программирование» в словосочетании «динамическое программирование» в действительности к «традиционному»программированию (написанию кода) почти никакого отношения не имеет и имеет смысл как в словосочетании «математическое программирование», которое является синонимом слова «оптимизация». Поэтому слово «программа» в данном контексте скорее означает оптимальную последовательность действий для получения решения задачи. К примеру, определенное расписание событий на выставке иногда называют программой. Программа в данном случае понимается как допустимая последовательность событий.

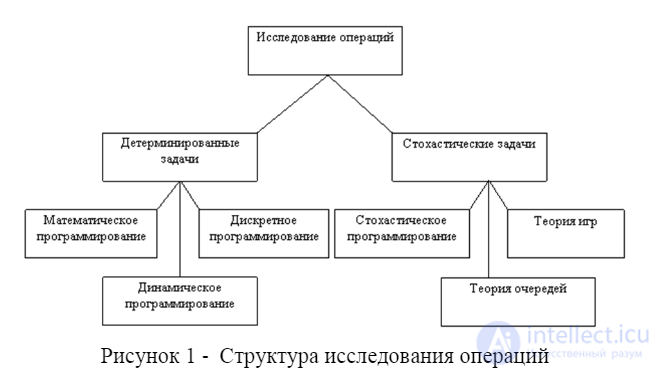
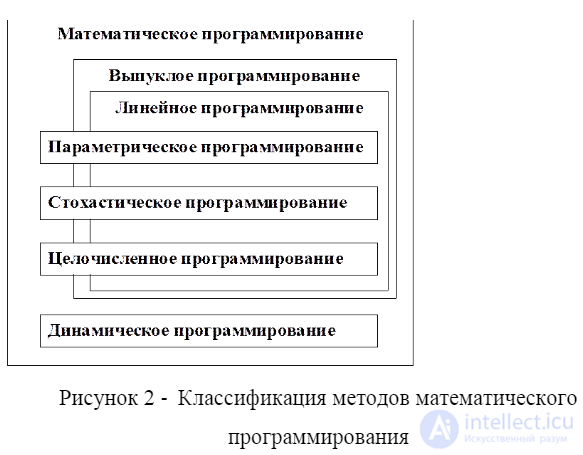
математическое программирование

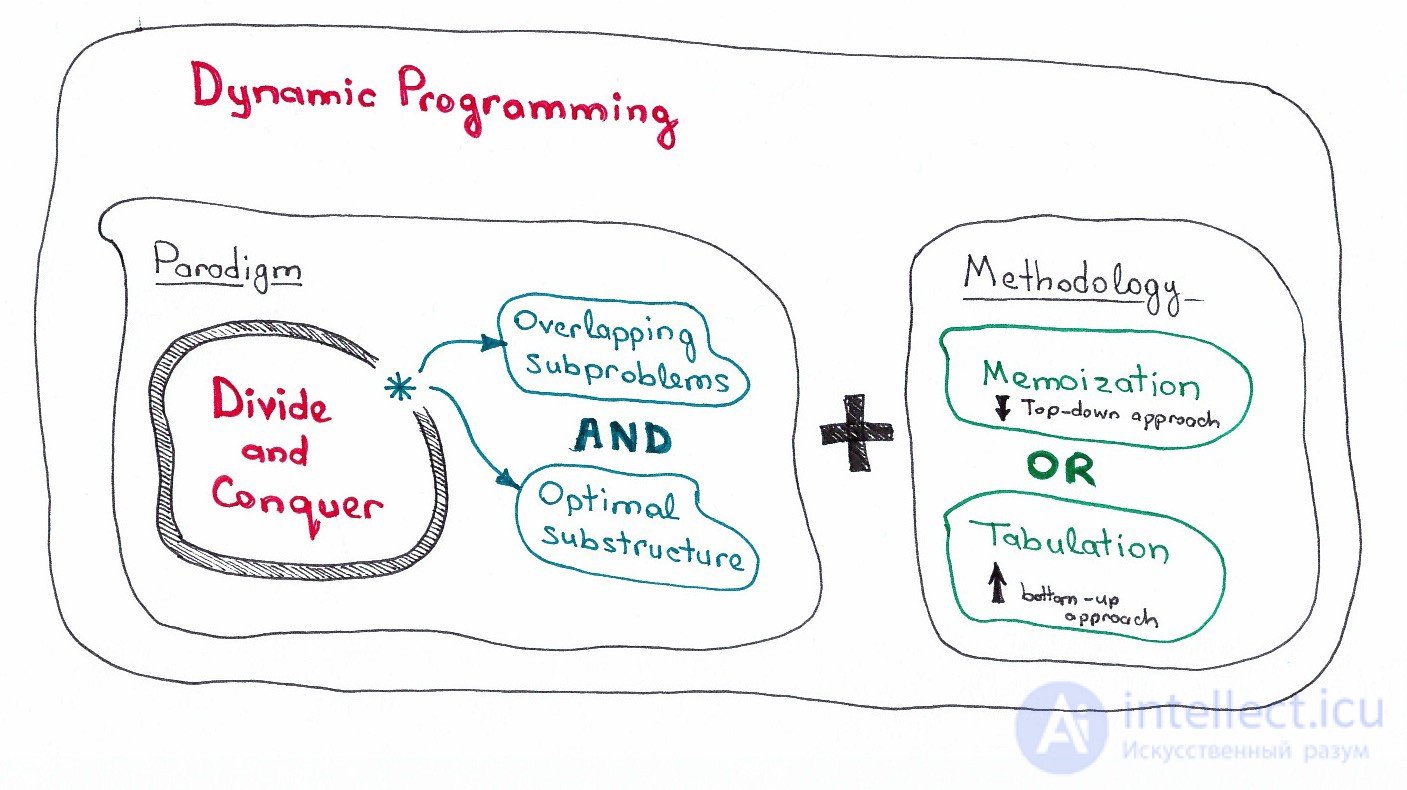
В динамическом программировании для управляемого процесса среди множества всех допустимых управлений ищут оптимальное в смысле некоторого критерия есть такое которое приводит к экстремальному (наибольшего или наименьшего) значения целевой функции - некоторой числовой характеристики процесса. Во многостепенность понимают или многоступенчатую структуру процесса, или распределения управления на ряд последовательных этапов (ступеней, шагов), соответствующих, как правило, различным моментам времени. Таким образом, в названии «Динамическое программирование» под «программированием» понимают «принятие решений» , «планирование» , а слово «динамическое» указывает на существенное значение времени и порядка выполнения операций в процессах и методах, которые рассматриваются.

Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач экспоненциально велико.

Метод динамического программирования сверху — это простое запоминание результатов решения тех подзадач, которые могут повторно встретиться в дальнейшем. Динамическое программирование снизу включает в себя переформулирование сложной задачи в виде рекурсивной последовательности более простых подзадач.

Методы динамического программирования является составной частью методов, используемых при исследовании операций и используются как в задачах оптимального планирования , так и при решении различных технических проблем (например, в задачах определения оптимальных размеров ступеней многоступенчатых ракет, в задачах оптимального проектирования прокладки дорог и др.)

Методы динамического программирования используются не только в дискретных , но и в непрерывных управляемых процессах, например, в таких процессах, когда в каждый момент определенного времени необходимо принимать решение. Динамическое программирование также дало новый подход к задачам вариационного исчисления .

Хотя метод динамического программирования существенно упрощает выходные задачи, и непосредственное его использование, как правило, связано с громоздкими вычислениями. Для преодоления этих трудностей разрабатываются приближенные методы динамического программирования.

Что такое динамическое программирование?

Динамическое программирование — метод решения задачи путем ее разбиения на несколько одинаковых подзадач, рекуррентно связанных между собой. Самым простым примером будут числа Фибоначчи — чтобы вычислить некоторое число в этой последовательности, нам нужно сперва вычислить третье число, сложив первые два, затем четвертое таким же образом на основе второго и третьего, и так далее

Как это использовать?

Решение задачи динамическим программированием должно содержать следующее:

• Зависимость элементов динамики друг от друга. Такая зависимость может быть прямо дана в условии (так часто бывает, если это задача на числовые последовательности). В противном случае вы можете попытаться узнать какой-то известный числовой ряд (вроде тех же чисел Фибоначчи), вычислив первые несколько значений вручную.
• Значение начальных состояний. В результате долгого разбиения на подзадачи вам необходимо свести функцию либо к уже известным значениям (как в случае с Фибоначчи — заранее определены первые два члена), либо к задаче, решаемой элементарно.

​Для решения задач методами динамического программирования нужно использовать рекурсию? они же медленные.

• Конечно, не надо, есть и другие подходы к реализации динамики.

История

Словосочетание «динамическое программирование» впервые было использовано в 1940-х годах Ричардом Беллманом для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения задачи, «предшествующей» ей. В 1953 году он уточнил это определение до современного. Первоначально эта область была основана, как системный анализ и инжиниринг, которая была признана IEEE. Вклад Беллмана в динамическое программирование был увековечен в названии уравнения Беллмана, центрального результата теории динамического программирования, который переформулирует оптимизационную задачу в рекурсивной форме.

Слово «программирование» в словосочетании «динамическое программирование» в действительности к «традиционному» программированию (написанию кода) почти никакого отношения не имеет и имеет смысл как в словосочетании «математическое программирование», которое является синонимом слова «оптимизация». Поэтому слово «программа» в данном контексте скорее означает оптимальную последовательность действий для получения решения задачи. К примеру, определенное расписание событий на выставке иногда называют программой. Программа в данном случае понимается как допустимая последовательность событий.

Идея динамического программирования

Классической задачей на последовательности является следующая.

Последовательность Фибоначчи Fn задается формулами: F1 = 1, F2 = 1,
Fn = Fn – 1 + Fn – 2 при n > 1. Необходимо найти Fn по номеру n.

Один из способов решения, который может показаться логичным и эффективным, — решение с помощью рекурсии:

int F(int n) {
 if (n < 2) return 1;
 else return F(n - 1) + F(n - 2);
}

Используя такую функцию, мы будем решать задачу «с конца» — будем шаг за шагом уменьшать n, пока не дойдем до известных значений.

Но как можно заметить, такая, казалось бы, простая программа уже при n = 40 работает заметно долго. Это связано с тем, что одни и те же промежуточные данные вычисляются по несколько раз — число операций нарастает с той же скоростью, с какой растут числа Фибоначчи — экспоненциально.

Один из выходов из данной ситуации — сохранение уже найденных промежуточных результатов с целью их повторного использования:

int F(int n) {
 if (A[n] != -1) return A[n];
 if (n < 2) return 1;
 else {
  A[n] = F(n - 1) + F(n - 2);
  return A[n];
 }
}

Приведенное решение является корректным и эффективным. Но для данной задачи применимо и более простое решение:

F  = 1;
F  = 1;
for (i = 2; i < n; i++) F[i] = F[i - 1] + F[i - 2];

Такое решение можно назвать решением «с начала» — мы первым делом заполняем известные значения, затем находим первое неизвестное значение (F3), потом следующее и т.д., пока не дойдем до нужного.

Именно такое решение и является классическим для динамического программирования: мы сначала решили все подзадачи (нашли все Fi для i < n), затем, зная решения подзадач, нашли ответ (Fn = Fn – 1 + Fn – 2, Fn – 1 и Fn – 2 уже найдены).

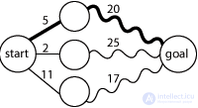
Нахождение кратчайшего пути в графе из одной вершины в другую, используя оптимальную подструктуру; прямая линия обозначает кратчайший путь между вершинами, которые она соединяет (промежуточные вершины пути не показаны); волнистая линия обозначает длинный путь; жирной линией обозначен итоговый кратчайший путь.

Граф подзадач (ребро означает, что одна задача зависит от решения другой) для чисел Фибоначчи (граф — ациклический).

Оптимальная подструктура в динамическом программировании означает, что оптимальное решение подзадач меньшего размера может быть использовано для решения исходной задачи. К примеру, кратчайший путь в графе из одной вершины (обозначим s) в другую (обозначим t) может быть найден так: сначала считаем кратчайший путь из всех вершин, смежных с s, до t, а затем, учитывая веса ребер, которыми s соединена со смежными вершинами, выбираем лучший путь до t (через какую вершину лучше всего пойти). В общем случае мы можем решить задачу, в которой присутствует оптимальная подструктура, проделывая следующие три шага.

1. Разбиение задачи на подзадачи меньшего размера.
2. Нахождение оптимального решения подзадач рекурсивно, проделывая такой же трехшаговый алгоритм.
3. Использование полученного решения подзадач для конструирования решения исходной задачи.

Подзадачи решаются делением их на подзадачи еще меньшего размера и т. Об этом говорит сайт https://intellect.icu . д., пока не приходят к тривиальному случаю задачи, решаемой за константное время (ответ можно сказать сразу). К примеру, если нам нужно найти n!, то тривиальной задачей будет 1! = 1 (или 0! = 1).

Перекрывающиеся подзадачи в динамическом программировании означают подзадачи, которые используются для решения некоторого количества задач (не одной) большего размера (то есть мы несколько раз проделываем одно и то же). Ярким примером является вычисление последовательности Фибоначчи, и — даже в таком тривиальном случае вычисления всего двух чисел Фибоначчи мы уже посчитали дважды. Если продолжать дальше и посчитать , т посчитается еще два раза, так как для вычисления будут нужны опять и . Получается следующее: простой рекурсивный подход будет расходовать время на вычисление решения для задач, которые он уже решал.

Чтобы избежать такого хода событий, мы будем сохранять решения подзадач, которые мы уже решали, и когда нам снова потребуется решение подзадачи, мы вместо того, чтобы вычислять его заново, просто достанем его из памяти. Этот подход называется мемоизацией. Можно проделывать и дальнейшие оптимизации — например, если мы точно уверены, что решение подзадачи нам больше не потребуется, можно выкинуть его из памяти, освободив ее для других нужд, или если процессор простаивает и мы знаем, что решение некоторых, еще не посчитанных подзадач, нам понадобится в дальнейшем, мы можем решить их заранее.

Подводя итоги вышесказанного можно сказать, что динамическое программирование пользуется следующими свойствами задачи:

• перекрывающиеся подзадачи;
• оптимальная подструктура;
• возможность запоминания решения часто встречающихся подзадач.

Динамическое программирование обычно придерживается двух подходов к решению задач:

• нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений уже решенных подзадач.
• восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи. Этот способ лучше нисходящего программирования в смысле размера необходимого стека и количества вызова функций, но иногда бывает нелегко заранее выяснить, решение каких подзадач нам потребуется в дальнейшем.

Языки программирования могут запоминать результат вызова функции с определенным набором аргументов (мемоизация), чтобы ускорить «вычисление по имени». В некоторых языках такая возможность встроена (например, Scheme, Common Lisp, Clojure, Perl, D), а в некоторых требует дополнительных расширений (C++).

Известны сериальное динамическое программирование, включенное во все учебники по исследованию операций, и несериальное динамическое программирование (НСДП), которое в настоящее время слабо известно, хотя было открыто в 1960-х годах.

Обычное динамическое программирование является частным случаем несериального динамического программирования, когда граф взаимосвязей переменных — просто путь. НСДП, являясь естественным и общим методом для учета структуры задачи оптимизации, рассматривает множество ограничений и/или целевую функцию как рекурсивно вычислимую функцию. Это позволяет находить решение поэтапно, на каждом из этапов используя информацию, полученную на предыдущих этапах, причем эффективность этого алгоритма прямо зависит от структуры графа взаимосвязей переменных. Если этот граф достаточно разрежен, то объем вычислений на каждом этапе может сохраняться в разумных пределах.

Одним из основных свойств задач, решаемых с помощью динамического программирования, является аддитивность. Неаддитивные задачи решаются другими методами. Например, многие задачи по оптимизации инвестиций компании являются неаддитивными и решаются с помощью сравнения стоимости компании при проведении инвестиций и без них.

Динамическое программирование в методах оптимизации

С точки зрения математической оптимизации, динамическое программирование заключается в упрощении нахождения общего оптимального развязку, путем поиска решений в подзадач, полученных разбиением задачи на последовательные промежутки времени. Это выражается в определении последовательности значений функций V 1 , V 2 , ..., V n , с аргументом y , который обозначает состояние системы в моменты времени i от 1 до n . Определением V n (y) является значение, полученное в состоянии y в конечный момент времени n . Значение V и в предыдущие моменты времениi = n -1, n - 2, ..., 2, 1 могут быть найдены двигаясь назад, используя рекурсивную зависимость , названную уравнения Беллмана . Для i = 2, ..., n , значение V i -1 для любого состояния y определяется с V i через максимизацию значение простой функции (как правило, суммы) выигрыша от решения в момент времени i - 1 и функции V i в новом состоянии системы, если бы это решение было воплощено. Поскольку V иуже было рассчитано для нужных состояний, тем выше приведена операция обеспечивает необходимое оптимальное значение V и -1 для этих состояний. Наконец, V 1 как исходное состояние системы является значением оптимального решения. Оптимальное значение переменных решения может быть восстановлено одно за другим выполнением обратных во времени вычислений.

Математическая оптимизация

С точки зрения математической оптимизации, динамическое программирование обычно означает упрощение решения путем разбиения его на последовательность шагов принятия решения с течением времени. Это делается путем определения последовательности функций значений V ₁ , V ₂ , ..., V _n, принимая y в качестве аргумента, представляющего состояние системы в моменты времени i от 1 до n . Определение V _n ( y ) - это значение, полученное в состоянии y в последний момент времени n . Значения V _i в более ранние времена i = n −1, n - 2, ..., 2, 1 можно найти, работая в обратном направлении, используя рекурсивное соотношение, называемое уравнением Беллмана . Для i = 2, ..., n , V _{i −1} в любом состоянии y вычисляется из V _i путем максимизации простой функции (обычно суммы) выигрыша от решения в момент времени i - 1 и функции V _i при новом состоянии системы, если это решение принято. Поскольку V _i уже вычислен для необходимых состояний, вышеупомянутая операция дает V _i−1 для этих состояний. Наконец, V ₁ в начальном состоянии системы является значением оптимального решения. Оптимальные значения переменных решения могут быть восстановлены одно за другим, отслеживая уже выполненные вычисления.

Теория управления

В теории управления типичной задачей является поиск допустимого управления что заставляет систему следовать допустимой траектории на непрерывном временном интервале что минимизирует функцию стоимости

Решение этой проблемы - оптимальный закон или политика управления. , что дает оптимальную траекторию и функция себестоимости . Последний подчиняется фундаментальному уравнению динамического программирования:

уравнение в частных производных, известное как уравнение Гамильтона – Якоби – Беллмана , в котором и . Обнаруживается, что минимизация с точки зрения , , а неизвестная функция а затем подставляет результат в уравнение Гамильтона – Якоби – Беллмана, чтобы получить решение уравнения в частных производных с граничным условием . На практике это обычно требует численных методов для некоторого дискретного приближения к точному соотношению оптимизации.

В качестве альтернативы непрерывный процесс можно аппроксимировать дискретной системой, что приводит к следующему рекуррентному соотношению, аналогичному уравнению Гамильтона – Якоби – Беллмана:

на -й этап равноотстоящие дискретные временные интервалы, и где и обозначим дискретные приближения к и . Это функциональное уравнение известно как уравнение Беллмана , которое может быть решено для точного решения дискретной аппроксимации уравнения оптимизации.

Пример из экономики: проблема Рамсея оптимального сбережения: модель Рэмси – Касса – Купманса.

В экономике цель обычно состоит в том, чтобы максимизировать (а не минимизировать) некоторую динамическую функцию общественного благосостояния . В задаче Рамсея эта функция связывает объемы потребления с уровнями полезности . Грубо говоря, планировщик сталкивается с компромиссом между одновременным потреблением и будущим потреблением (через инвестиции в основной капитал, который используется в производстве), известный как межвременной выбор . Будущее потребление дисконтируется по постоянной ставке.. Дискретное приближение к уравнению перехода капитала дается выражением

где потребление, это капитал, и является производственной функцией, удовлетворяющей условиям Инада . Первоначальный основной капитал предполагается.

Позволять быть потреблением в период t , и предположим, что потребление дает полезность пока живет потребитель. Предположим, что потребитель нетерпелив, поэтому он дисконтирует будущую полезность с коэффициентом b каждый период, где. Позволятьбыть капиталом в период t . Предположим, что начальный капитал - это заданная сумма., и предположим, что капитал и потребление этого периода определяют капитал следующего периода как , где A - положительная постоянная, а. Предположим, что капитал не может быть отрицательным. Тогда задачу решения потребителя можно записать следующим образом:

при условии для всех

Написанная таким образом задача выглядит сложной, потому что она включает решение для всех переменных выбора. . (Столица не является переменной выбора - первоначальный капитал потребителя принимается заданным.)

Подход динамического программирования для решения этой проблемы включает разбиение ее на последовательность более мелких решений. Для этого мы определяем последовательность функций значения , за которые представляют ценность наличия любого количества капитала k в каждый момент времени t . Нет (по предположению) никакой пользы от наличия капитала после смерти,.

Стоимость любого количества капитала в любой предыдущий момент может быть рассчитана методом обратной индукции с использованием уравнения Беллмана . В этой задаче для каждого, уравнение Беллмана имеет вид

при условии

Эта задача намного проще, чем та, которую мы записали ранее, потому что она включает только две переменные решения: и . Интуитивно, вместо того, чтобы выбирать план на всю жизнь при рождении, потребитель может делать что-то шаг за шагом. В момент t его текущий капитал дан, и ему нужно только выбрать потребление тока и экономия .

Чтобы решить эту проблему, мы работаем в обратном направлении. Для простоты текущий уровень капитала обозначен как k . уже известно, поэтому, используя уравнение Беллмана, как только мы сможем вычислить и так далее, пока не дойдем до , что является значением задачи начального решения на все время жизни. Другими словами, как только мы узнаем, мы можем вычислить , что является максимумом , где переменная выбора и .

Работая в обратном направлении, можно показать, что функция ценности во времени является

где каждый является константой, и это оптимальное количество, которое нужно потреблять за раз является

который можно упростить до

Мы видим, что оптимально потреблять большую часть текущего богатства по мере того, как человек становится старше, в конечном итоге потребляя все оставшееся богатство в периоде T , последнем периоде жизни.

Компьютерное программирование

Есть два ключевых атрибута, которые проблема должна иметь для того, чтобы динамическое программирование было применимо: оптимальная подструктура и перекрывающиеся подзадачи . Если проблема может быть решена путем комбинирования оптимальных решений неперекрывающихся подзадач, стратегия вместо этого называется « разделяй и властвуй ». Вот почему сортировка слиянием и быстрая сортировка не относятся к задачам динамического программирования.

Оптимальная подструктура означает, что решение данной задачи оптимизации может быть получено путем комбинации оптимальных решений ее подзадач. Такие оптимальные подструктуры обычно описываются с помощью рекурсии . Например, для графа G = (V, E) кратчайший путь p от вершины u до вершины v имеет оптимальную подструктуру: возьмите любую промежуточную вершину w на этом кратчайшем пути p . Если p действительно является кратчайшим путем, то его можно разделить на подпути p ₁ от u до w и p ₂ отw к v , так что они, в свою очередь, действительно являются кратчайшими путями между соответствующими вершинами (с помощью простого аргумента вырезания и вставки, описанного во введении в алгоритмы ). Следовательно, можно легко сформулировать решение для поиска кратчайших путей рекурсивным способом, что и делает алгоритм Беллмана – Форда или алгоритм Флойда – Уоршалла .

Перекрывающиеся подзадачи означают, что пространство подзадач должно быть небольшим, то есть любой рекурсивный алгоритм, решающий проблему, должен решать одни и те же подзадачи снова и снова, а не генерировать новые подзадачи. Например, рассмотрим рекурсивную формулировку для генерации ряда Фибоначчи: F _i = F _{i −1} + F _{i −2} с базовым случаем F ₁ = F ₂ = 1. Тогда F ₄₃ = F ₄₂ + F ₄₁ и F ₄₂ = F ₄₁ + F₄₀ . Теперь F ₄₁ решается в рекурсивных поддеревьях как F _43, так и F ₄₂ . Несмотря на то, что общее количество подзадач на самом деле невелико (всего 43 из них), мы в конечном итоге решаем одни и те же проблемы снова и снова, если примем наивное рекурсивное решение, подобное этому. Динамическое программирование учитывает этот факт и решает каждую подзадачу только один раз.

Рисунок 2. Граф подзадач для последовательности Фибоначчи. Тот факт, что это не дерево, указывает на перекрывающиеся подзадачи.

Этого можно добиться двумя способами:

• Подход «сверху вниз» : это прямой результат рекурсивной постановки любой проблемы. Если решение любой проблемы может быть сформулировано рекурсивноиспользованием раствора для его подзадач, и если ее подзадачи накладываются другдруге, то можно легко memoize или хранить решения для подзадачи в таблице. Каждый раз, когда мы пытаемся решить новую подзадачу, мы сначала проверяем таблицу, чтобы увидеть, решена ли она уже. Если решение было записано, мы можем использовать его напрямую, в противном случае мы решаем подзадачу и добавляем ее решение в таблицу.
• Подход снизу вверх : как только мы рекурсивно сформулируем решение проблемы, как в терминах его подзадач, мы можем попытаться переформулировать проблему снизу вверх: попробуйте сначала решить подзадачи и использовать их решения для построения: и найти решения для более серьезных подзадач. Это также обычно делается в табличной форме, итеративно генерируя решения все больших и больших подзадач, используя решения небольших подзадач. Например, если мы уже знаем значения F ₄₁ и F ₄₀ , мы можем напрямую вычислить значение F ₄₂ .

Некоторые языки программирования могут автоматически запоминать результат вызова функции с определенным набором аргументов, чтобы ускорить вычисление вызова по имени (этот механизм называется вызовом по необходимости ). Некоторые языки делают это возможным переносимым (например, Scheme , Common Lisp , Perl или D ). Некоторые языки имеют встроенную автоматическую мемоизацию , например табличный Пролог и J , который поддерживает мемоизацию с помощью наречия M. В любом случае это возможно только для ссылочно прозрачногофункция. Мемоизация также встречается как легкодоступный шаблон проектирования в языках, основанных на перезаписи терминов, таких как Wolfram Language .

Биоинформатика

Динамическое программирование широко используется в биоинформатике для таких задач, как выравнивание последовательностей , сворачивание белков , предсказание структуры РНК и связывание белок-ДНК. Первые алгоритмы динамического программирования для связывания белка с ДНК были разработаны в 1970-х независимо Чарльзом ДеЛизи в США и Георгием Гурским и Александром Заседателевым в СССР. В последнее время эти алгоритмы стали очень популярными в биоинформатике и вычислительной биологии , особенно в исследованиях позиционирования нуклеосом и связывания факторов транскрипции .

Классические задачи динамического программирования

• Задача о наибольшей общей подпоследовательности: даны две последовательности, требуется найти самую длинную общую подпоследовательность.
• Задача поиска наибольшей увеличивающейся подпоследовательности: дана последовательность, требуется найти самую длинную возрастающую подпоследовательность.
• Задача о редакционном расстоянии (расстояние Левенштейна): даны две строки, требуется найти минимальное количество стираний, замен и добавлений символов, преобразующих одну строку в другую.
• Задача о вычислении чисел Фибоначчи
• Задача о порядке перемножения матриц: даны матрицы A₁, …,An, требуется минимизировать количество скалярных операций для их перемножения.
• Задача о выборе траектории
• Задача последовательного принятия решения
• Задача об использовании рабочей силы
• Задача управления запасами
• Задача о ранце: из неограниченного множества предметов со свойствами «стоимость» и «вес» требуется отобрать некое число предметов таким образом, чтобы получить максимальную суммарную стоимость при ограниченном суммарном весе.
• Алгоритм Флойда - Уоршелла: найти кратчайшие расстояния между всеми вершинами взвешенного ориентированного графа.
• Алгоритм Беллмана - Форда: найти кратчайший путь во взвешенном графе между двумя заданными вершинами.
• Максимальное независимое множество вершин в дереве: дано дерево, найти максимальное множество вершин, никакие две из которых не связаны ребром.

Вау!! 😲 Ты еще не читал? Это зря!

• Алгоритм Беллмана - Форда
• Алгоритм Витерби
• Алгоритм Данцига
• Алгоритм динамической трансформации временной шкалы
• Алгоритм Кока - Янгера - Касами
• Алгоритм Нидлмана - Вунша
• Алгоритм прямого-обратного хода
• Алгоритм Смита - Ватермана
• Алгоритм Флойда - Уоршелла
• Алгоритм Эрли
• Задача о независимом множестве
• Задача о порядке перемножения матриц
• Задача о рюкзаке
• Задача о сумме подмножеств
• Задача поиска наибольшей увеличивающейся подпоследовательности
• Марковский момент
• Марковский процесс принятия решений
• Наибольшая общая подпоследовательность
• Обратная индукция
• Поиск похожих строк
• Расстояние Дамерау - Левенштейна
• Расстояние Левенштейна
• Уравнение Беллмана

• Выпуклость в экономике
• Жадный алгоритм
• Невыпуклость ( экономика )
• Стохастическое программирование
• Стохастическое динамическое программирование
• Обучение с подкреплением
• нелинейное программирование ,

А как ты думаешь, при улучшении динамическое программирование, будет лучше нам? Надеюсь, что теперь ты понял что такое динамическое программирование и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов