Лекция
Привет, сегодня поговорим про вычислительная сложность, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое вычислительная сложность , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
Вычисли́тельная сло́жность — понятие в информатике и теории алгоритмов, обозначающее функцию зависимости объема работы, выполняемой некоторым алгоритмом, от размера входных данных. Раздел, изучающий вычислительную сложность, называется теорией сложности вычислений. Объем работы обычно измеряется абстрактными понятиями времени и пространства, называемыми вычислительными ресурсами. Время определяется количеством элементарных шагов, необходимых для решения задачи, тогда как пространство определяется объемом памяти или места на носителе данных. Таким образом, в этой области предпринимается попытка ответить на центральный вопрос разработки алгоритмов: «как изменится время исполнения и объем занятой памяти в зависимости от размера входа?». Здесь под размером входа понимается длина описания данных задачи в битах (например, в задаче коммивояжера длина входа почти пропорциональна количеству городов и дорог между ними), а под размером выхода — длина описания решения задачи (наилучшего маршрута в задаче коммивояжера).
В частности, теория сложности вычислений определяет NP-полные задачи, которые недетерминированная машина Тьюринга может решить за полиномиальное время, тогда как для детерминированной машины Тьюринга полиномиальный алгоритм неизвестен. Обычно это сложные задачи оптимизации, например, задача коммивояжера.
С теоретической информатикой тесно связаны такие области как алгоритмический анализ и теория вычислимости. Связующим звеном между теоретической информатикой и алгоритмическим анализом является тот факт, что их формирование посвящено анализу необходимого количества ресурсов определенных алгоритмов решения задач, тогда как более общим вопросом является возможность использования алгоритмов для подобных задач. Конкретизируясь, попытаемся классифицировать проблемы, которые могут или не могут быть решены при помощи ограниченных ресурсов. Сильное ограничение доступных ресурсов отличает теорию вычислительной сложности от вычислительной теории, последняя отвечает на вопрос какие задачи, в принципе, могут быть решены алгоритмически.
Теория сложности вычислений возникла из потребности сравнивать быстродействие алгоритмов, четко описывать их поведение (время исполнения и объем необходимой памяти) в зависимости от размера входа.
Количество элементарных операций, затраченных алгоритмом для решения конкретного экземпляра задачи, зависит не только от размера входных данных, но и от самих данных. Например, количество операций алгоритма сортировки вставками значительно меньше в случае, если входные данные уже отсортированы. Чтобы избежать подобных трудностей, рассматривают понятие временной сложности алгоритма в худшем случае.
Временная сложность алгоритма (в худшем случае) — это функция от размера входных данных, равная максимальному количеству элементарных операций, проделываемых алгоритмом для решения экземпляра задачи указанного размера.
Аналогично понятию временной сложности в худшем случае определяется понятие временная сложность алгоритма в наилучшем случае. Также рассматривают понятие среднее время работы алгоритма, то есть математическое ожидание времени работы алгоритма. Иногда говорят просто: «Временная сложность алгоритма» или «Время работы алгоритма», имея в виду временную сложность алгоритма в худшем, наилучшем или среднем случае (в зависимости от контекста).
По аналогии с временной сложностью, определяют пространственную сложность алгоритма, только здесь говорят не о количестве элементарных операций, а об объеме используемой памяти.
Несмотря на то, что функция временной сложности алгоритма в некоторых случаях может быть определена точно, в большинстве случаев искать точное ее значение бессмысленно. Об этом говорит сайт https://intellect.icu . Дело в том, что во-первых, точное значение временной сложности зависит от определения элементарных операций (например, сложность можно измерять в количестве арифметических операций, битовых операций или операций на машине Тьюринга), а во-вторых, при увеличении размера входных данных вклад постоянных множителей и слагаемых низших порядков, фигурирующих в выражении для точного времени работы, становится крайне незначительным.
Рассмотрение входных данных большого размера и оценка порядка роста времени работы алгоритма приводят к понятию асимптотической сложности алгоритма. При этом алгоритм с меньшей асимптотической сложностью является более эффективным для всех входных данных, за исключением лишь, возможно, данных малого размера. Для записи асимптотической сложности алгоритмов используются асимптотические обозначения:
| Обозначение | Интуитивное объяснение | Определение |
|---|---|---|
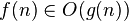 |
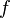 ограничена сверху функцией ограничена сверху функцией 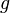 (с точностью до постоянного множителя) асимптотически (с точностью до постоянного множителя) асимптотически |
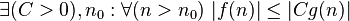 или или 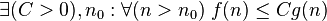 |
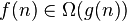 |
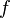 ограничена снизу функцией ограничена снизу функцией 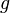 (с точностью до постоянного множителя) асимптотически (с точностью до постоянного множителя) асимптотически |
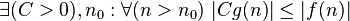 |
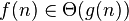 |
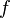 ограничена снизу и сверху функцией ограничена снизу и сверху функцией 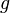 асимптотически асимптотически |
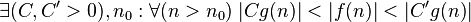 |
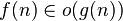 |
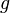 доминирует над доминирует над 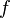 асимптотически асимптотически |
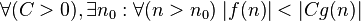 |
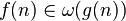 |
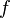 доминирует над доминирует над 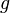 асимптотически асимптотически |
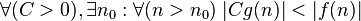 |
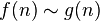 |
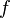 эквивалентна эквивалентна 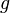 асимптотически асимптотически |
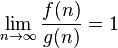 |
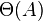 ), то есть на ковер, площадь которого больше в два раза, уйдет в два раза больше времени. Соответственно, при увеличении площади ковра в сто тысяч раз, объем работы увеличивается строго пропорционально в сто тысяч раз, и т. п.
), то есть на ковер, площадь которого больше в два раза, уйдет в два раза больше времени. Соответственно, при увеличении площади ковра в сто тысяч раз, объем работы увеличивается строго пропорционально в сто тысяч раз, и т. п.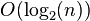 ), так как открыв книгу примерно в середине, мы уменьшаем размер «оставшейся проблемы» вдвое (за счет сортировки имен по алфавиту). Таким образом, в книге, толщиной в 1000 страниц, любое имя находится не больше чем за
), так как открыв книгу примерно в середине, мы уменьшаем размер «оставшейся проблемы» вдвое (за счет сортировки имен по алфавиту). Таким образом, в книге, толщиной в 1000 страниц, любое имя находится не больше чем за 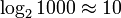 раз (открываний книги). При увеличении объема страниц до ста тысяч, проблема все еще решается за
раз (открываний книги). При увеличении объема страниц до ста тысяч, проблема все еще решается за 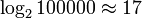 заходов. (См. Двоичный поиск .)
заходов. (См. Двоичный поиск .)Поскольку 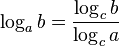 , в асимптотической оценке сложности часто пишут « логарифм » без упоминания основания — например,
, в асимптотической оценке сложности часто пишут « логарифм » без упоминания основания — например,  .
.
Необходимо подчеркнуть, что степень роста наихудшего времени выполнения — не единственный или самый важный критерий оценки алгоритмов и программ. Приведем несколько соображений, позволяющих посмотреть на критерий времени выполнения с других точек зрения:
Если создаваемая программа будет использована только несколько раз, тогда стоимость написания и отладки программы будет доминировать в общей стоимости программы, то есть фактическое время выполнения не окажет существенного влияния на общую стоимость. В этом случае следует предпочесть алгоритм, наиболее простой для реализации.
Если программа будет работать только с «малыми» входными данными, то степень роста времени выполнения будет иметь меньшее значение, чем константа, присутствующая в формуле времени выполнения[1]. Вместе с тем и понятие «малости» входных данных зависит от точного времени выполнения конкурирующих алгоритмов. Существуют алгоритмы, такие как алгоритм целочисленного умножения, асимптотически самые эффективные, но которые никогда не используют на практике даже для больших задач, так как их константы пропорциональности значительно превосходят подобные константы других, более простых и менее «эффективных» алгоритмов. Другой пример — фибоначчиевы кучи, несмотря на асимптотическую эффективность, с практической точки зрения программная сложность реализации и большие значения констант в формулах времени работы делают их менее привлекательными, чем обычные бинарные деревья [1].
 |
Если решение некоторой задачи для n-вершинного графа при одном алгоритме занимает время (число шагов) порядка nC, а при другом — порядка n+n!/C, где C — постоянное число , то согласно «полиномиальной идеологии» первый алгоритм практически эффективен, а второй — нет, хотя, например, при С=10(1010) дело обстоит как раз наоборот.[2]
А. А. Зыков
|
 |
Эффективные, но сложные алгоритмы могут быть нежелательными, если готовые программы будут поддерживать лица, не участвующие в написании этих программ.
Известны примеры, когда эффективные алгоритмы требуют таких больших объемов машинной памяти (без возможности использования более медленных внешних средств хранения), что этот фактор сводит на нет преимущество «эффективности» алгоритма. Таким образом, часто важна не только «сложность по времени», но и «сложность по памяти» (пространственная сложность).
В численных алгоритмах точность и устойчивость алгоритмов не менее важны, чем их временная эффективность.
Класс сложности — это множество задач распознавания, для решения которых существуют алгоритмы, схожие по вычислительной сложности. Два важных представителя:
Класс P вмещает все те проблемы, решение которых считается «быстрым», то есть время решения которых полиномиально зависит от размера входа. Сюда относитсясортировка, поиск во множестве, выяснение связности графов и многие другие.
Класс NP содержит задачи, которые недетерминированная машина Тьюринга в состоянии решить за полиномиальное количество шагов от размера входных данных. Следует заметить, что недетерминированная машина Тьюринга является лишь абстрактной моделью, в то время как современные компьютеры соответствуютдетерминированной машине Тьюринга с ограниченной памятью. Поскольку детерминированная машина Тьюринга может рассматриваться как специальный случайнедетерминированной машины Тьюринга , класс NP включает в себя класс P , а также некоторые проблемы, для решения которых известны лишь алгоритмы , экспоненциально зависящие от размера входа (то есть неэффективные для больших входов). В класс NP входят многие знаменитые проблемы, такие как задача коммивояжера , задача выполнимости булевых формул, факторизация и др.
Вопрос о равенстве этих двух классов считается одной из самых сложных открытых проблем в области теоретической информатики. Математический институт Клэявключил эту проблему в список проблем тысячелетия, предложив награду размером в один миллион долларов США за ее решение.
Надеюсь, эта статья про вычислительная сложность, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое вычислительная сложность и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов