Лекция
Привет, Вы узнаете о том , что такое плоский прямолинейный граф, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое плоский прямолинейный граф, пплг, рсдс , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
Плоский прямолинейный граф ( ППЛГ ) — термин используемый в вычислительной геометрии для вложения планарного графа на плоскости так, что его ребра переходят в прямолинейные отрезки. Теорема Фари (1948) утверждает, что каждый планарный граф имеет такой тип вложения.
Планарный граф, уложенный на плоскости, принято называть плоским. Плоская укладка планарного графа G=(V,E) — это отображение каждой вершины из V в точку на плоскости, а каждого ребра из E в простую линию, соединяющую пару образов концевых вершин этого ребра так, чтобы образы ребер пересекались только в своих концевых точках. Хорошо известно, что любой планарный граф можно уложить на плоскости так, чтобы все ребра отобразились в прямолинейные отрезки.
В вычислительной геометрии ППЛГ часто называют плоским разбиением , с предположением или утверждением, что разбиение полигонально. Максимальным плоским разбиением называют такое разбиение, что невозможно добавить ни одно ребро, объединяющее две вершины, так чтобы не нарушить плоскость.
ППЛГ без вершин 1 степени определяет разбиение плоскости на полигональные регионы и наоборот. Отсутствие вершин 1 степени упрощает описание многих алгоритмов, но это не существенно.
ППЛГ может служить как представление разнообразных карт . К примеру, географическая карта в геоинформационной системе .
Особым случаем ППЛГ являются триангуляция : триангуляция многоугольника , триангуляция множества точек . Многоточечная триангуляция является максимальной ППЛГ в том смысле, что невозможно прибавить к ним прямолинейные ребра, так чтобы граф остался планарным. Триангуляции имеют многочисленные применения в разных областях.
ППЛГ может рассматриваться как особый вид евклидовых графов . Однако в дискуссиях, связанных с евклидовыми графами основной интерес представляет их метрические свойства, то есть расстояния между вершинами, в то время как для ППЛГ основной интерес связан с топологическими свойствами. Для некоторых графов, таких как триангуляция Делоне , как метрические, так и топологические свойства имеют немаловажное значение.
Реберный список с двойными связями особенно удобен для представления ППЛГ. Пусть задан граф G=(V,E) V={v1,v2...vn} а E={e1,e2...en} . Об этом говорит сайт https://intellect.icu . Главная компонента РСДС для планарного графа это реберный узел. Между ребрами графа и реберными узлами РСДС существует взаимно однозначное соответствие, т.е. каждое ребро представлено в РСДС ровно один раз. Реберный узел РСДС, соответствующий ребру графа, например, ek={v1,v2} имеет 4 поля (V1,V2,F1,F2 ) и 2 указателя (P1,P2 ). Поле V1 содержит начало ребра, а поле V2 содержит его конец (так изначально неориентированное ребро получает условную ориентацию). Поля F1 и F2 содержат имена граней, лежащих слева и справа от ориентированного ребра (v1,v2 ). Указатель P1 (соответственно P2 ) задает реберный узел, содержащий первое ребро, встречаемое вслед за ребром (v1,v2 ), при повороте от него против часовой стрелки вокруг v1 (соответственно v2 ).
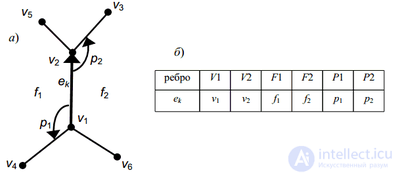
Представление плоского графа с помощью РСДС
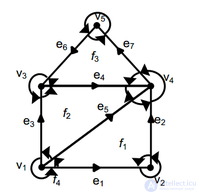
Плоский граф, ребрам которого придана произвольная ориентация для представления его с помощью РСДС. Стрелки вокруг вершин соответствуют указателям (P1, P2)
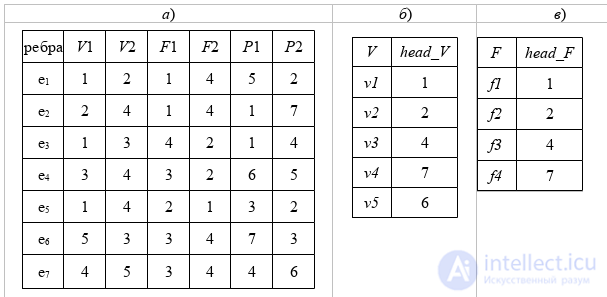
(а) РСДС, (б) входы по вершинам head_V [1..n] и (в) входы по граням head_F[1..l]
РСДС — Реберный список с двойными связями.
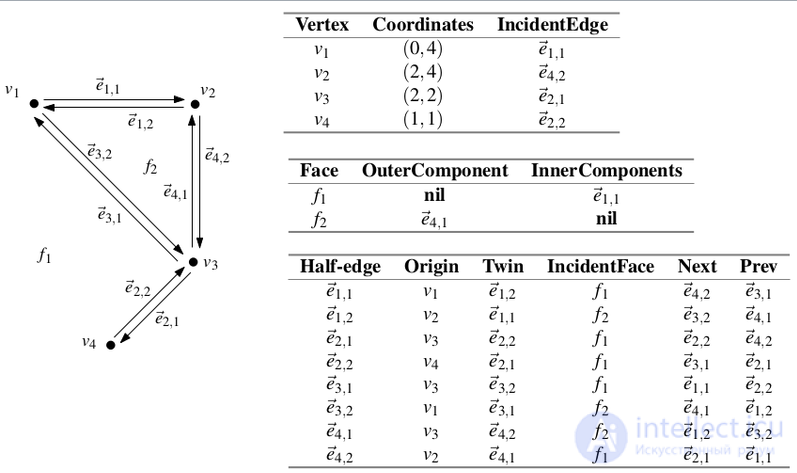
Ко второму описанию
РСДС состоит из 3 компонент:
struct vertex {
x, y;
half_edge *rep; /* rep->origin == this */
};
struct face {
half_edge *out;
list in;
};
struct half_edge {
half_edge *prev; /* prev->next == this */
half_edge *next; /* next->prev == this */
half_edge *twin; /* twin->twin == this */
vertex *origin; /* twin->next->origin == origin &&
prev->twin->origin == origin */
face *incident_face; /* prev->incident_face == incident_face &&
next->incident_face == incident_face */
};
нужно переписать сюда соответствующую главу из де Берга.
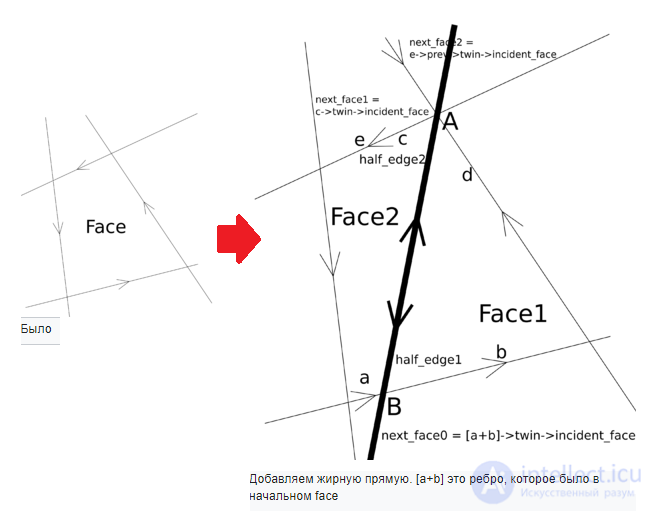
У нас есть множество прямых. Мы хотим представить это множество в виде РСДС.
Будем добавлять прямые по одной. Изначально у нас есть фэйс, который представляет собой всю плоскость. Алгоритм будет такой:
Вот эти ссылки надо не забыть поменять:
half_edge1->origin = A; half_edge2->origin = B; half_edge1->twin = half_edge2; half_edge2->twin = half_edge1; half_edge1->incident_face = face1; half_edge2->incident_face = face2; half_edge1->next = b; b->prev = half_edge1; half_edge1->prev = d; d->next = half_edge1; half_edge2->next = c; c->prev = half_edge2; half_edge2->prev = a; a->next = half_edge2;
Исследование, описанное в статье про плоский прямолинейный граф, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое плоский прямолинейный граф, пплг, рсдс и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Из статьи мы узнали кратко, но содержательно про плоский прямолинейный граф
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов