Раскраска графа кратко

Привет, сегодня поговорим про раскраска графа, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое раскраска графа , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

Разнообразные задачи, возникающие при планировании производства, составлении графиков осмотра, хранении и транспортировке товаров и т. д., могут быть представлены часто как задачи теории графов, тесно связанные с так называемой «задачей раскраски». Графы, рассматриваемые в этой части, являются неориентированными и не имеют петель.

Пусть G = (V, Е) — произвольный граф и {ci, ..., ct} — некоторое множество, элементы которого будем называть красками. t-раскраской графа G называется отображение ф из V В {ci, ..., ct} такое, что для любых двух различных смежных вершин и и v графа G выполняется ф(u) != ф(v). Об этом говорит сайт https://intellect.icu .
Отметим, что здесь не предполагается, что ф отображает V на все множество красок {ci, ..., ct}. Будем говорить, что цвет ф(v) приписан вершине v G V или вершина v имеет цвет ф(v). Мы видим, что t- раскраска графа G приписывает каждой его вершине один из t заданных цветов таким образом, что любые две различные смежные вершины имеют разный цвет.

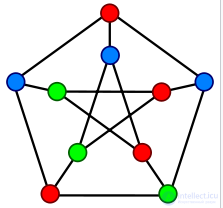
Трехцветовая раскраска графа Петерсена

Граф называется t-раскрашиваемым, если он обладает t-раскраской. Граф называется t-хроматическим, если он t-раскрашиваемый, но не является (t — 1)-раскрашиваемым; число t в таком случае называют хроматическим числом графа G и обозначают через x(G).

Заметим, что
1) 1-хроматичсскис графы — это нулевые графы и только они;
2) 2-хроматические графы — это ненулевые двудольные графы и только они;
3) х(Kn) = n и x(G) >= n если граф G содержит в качестве подграфа граф Кn для натурального числа n.

Задача нахождения хроматического числа произвольного графа явилась предметом многих исследований в конце XIX и в текущем столетии. Сейчас по этому вопросу известно большое количество интересных результатов. В этом разделе мы рассмотрим «приближенный» алгоритм, позволяющий находить значение хроматического числа произвольного графа и соответствующую этому значению раскраску вершин.

На этом все! Теперь вы знаете все про раскраска графа, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое раскраска графа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов