Теория алгоритмов

Привет, сегодня поговорим про теория алгоритмов, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое теория алгоритмов, алгоритм, классы сложности , класс сложности , теория вычислимости , теория сложности, теория автоматов , класс сложности p , класс сложности np , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

теория алгоритм ов — раздел информатики, изучающий общие свойства и закономерности алгоритмов и разнообразные формальные модели их представления. К задачам теории алгоритмов относятся формальное доказательство алгоритмической неразрешимости задач, асимптотический анализ сложности алгоритмов, классификация алгоритмов в соответствии с классами сложности, разработка критериев сравнительной оценки качества алгоритмов и т. п. Вместе с математической логикой теория алгоритмов образует теоретическую основу вычислительных наук.

Теория алгоритмов — наука, находящаяся на стыке математики и информатики, изучающая общие свойства и закономерности алгоритмов и разнообразные формальные модели их представления. К задачам теории алгоритмов относятся формальное доказательство алгоритмической неразрешимости задач, асимптотический анализ сложности алгоритмов, классификация алгоритмов в соответствии с классами сложности, разработка критериев сравнительной оценки качества алгоритмов и т. п.

Возникновение теории алгоритмов

Развитие теории алгоритмов начинается с доказательства К. Геделем теорем о неполноте формальных систем, включающих арифметику, первая из которых была доказана в 1931 г. Возникшее в связи с этими теоремами предположение о невозможности алгоритмического разрешения многих математических проблем (в частности, проблемы выводимости в исчислении предикатов) вызвало необходимость стандартизации понятия алгоритма. Первые стандартизованные варианты этого понятия были разработаны в 30-х годах XX века в работах А. Тьюринга, А. Черча и Э. Поста. Предложенные ими машина Тьюринга, машина Поста и лямбда-исчисление Черча оказались эквивалентными друг другу. Основываясь на работах Геделя, С. Клини ввел понятие рекурсивной функции, также оказавшееся эквивалентным вышеперечисленным.

Одним из наиболее удачных стандартизованных вариантов алгоритма является введенное А. А. Марковым понятие нормального алгоритма. Оно было разработано десятью годами позже работ Тьюринга, Поста, Черча и Клини в связи с доказательством алгоритмической неразрешимости ряда алгебраических проблем.

Следует отметить также немалый вклад в теорию алгоритмов, сделанный Д. Кнутом, A. Ахо и Дж. Ульманом. Одной из лучших работ на эту тему является книга «Алгоритмы: построение и анализ» Томаса Х. Кормена, Чарльза И. Лейзерсона, Рональда Л. Ривеста, Клиффорда Штайна.

Модели вычислений

• Машина Тьюринга — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма. Машина Тьюринга является расширением конечного автомата и, согласно тезису Черча — Тьюринга, способна имитировать все другие исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
• Лямбда-исчисление — рассматривается пара — λ-выражение и его аргумент, — а вычислением считается применение, или апплицирование, первого члена пары ко второму. Это позволяет отделить функцию и то, к чему она применяется. В более общем случае вычислением считаются цепочки, начинающиеся с исходного λ-выражения, за которым следут конечная последовательность λ-выражений, каждое из которых получается из предыдущего применением β-редукции, то есть правила подстановки.
• Комбинаторная логика — трактовка вычисления сходна с λ-исчислением, но имеются и важные отличия (например, комбинатор неподвижной точки Y имеет нормальную форму в комбинаторной логике, а в λ-исчислении — не имеет). Комбинаторная логика была первоначально разработана для изучения природы парадоксов и для построения концептуально ясных оснований математики, причем представление о переменной исключалось вовсе, что помогало прояснить роль и место переменных в математике.
• Регистровые машины (англ.)
  • RAM-машина — абстрактная вычислительная машина, моделирующая компьютер с произвольным доступом к памяти. Именно эта модель вычислений наиболее часто используется при анализе алгоритмов.

Тезис Черча — Тьюринга и алгоритмически неразрешимые проблемы

Алан Тьюринг высказал предположение (известное как Тезис Черча — Тьюринга), что любой алгоритм в интуитивном смысле этого слова может быть представлен эквивалентной машиной Тьюринга. Уточнение представления о вычислимости на основе понятия машины Тьюринга (и других эквивалентных ей понятий) открыло возможности для строгого доказательства алгоритмической неразрешимости различных массовых проблем (то есть проблем о нахождении единого метода решения некоторого класса задач, условия которых могут варьироваться в известных пределах). Простейшим примером алгоритмически неразрешимой массовой проблемы является так называемая проблема применимости алгоритма (называемая также проблемой остановки). Она состоит в следующем: требуется найти общий метод, который позволял бы для произвольной машины Тьюринга (заданной посредством своей программы) и произвольного начального состояния ленты этой машины определить, завершится ли работа машины за конечное число шагов, или же будет продолжаться неограниченно долго.

В течение первого десятилетия истории теории алгоритмов неразрешимые массовые проблемы были обнаружены лишь внутри самой этой теории (сюда относится описанная выше проблема применимости), а также внутри математической логики (проблема выводимости в классическом исчислении предикатов). Поэтому считалось, что теория алгоритмов представляет собой обочину математики, не имеющую значения для таких ее классических разделов, как алгебра или анализ. Положение изменилось после того, как А. А. Марков и Э. Л. Пост в 1947 году установили алгоритмическую неразрешимость известной в алгебре проблемы равенства для конечнопорожденных и конечноопределенных полугрупп (т. н. проблемы Туэ). Впоследствии была установлена алгоритмическая неразрешимость и многих других «чисто математических» массовых проблем. Одним из наиболее известных результатов в этой области является доказанная Ю. В. Матиясевичем алгоритмическая неразрешимость десятой проблемы Гильберта.

Направления и разделы

Теория алгоритмов развивается, главным образом, по трем направлениям:

• Классическое:
  • Формальная формулировка задач;
  • Понятие проблемы разрешения;
  • Классификация уровней сложности («P», «NP» и другие).
• Анализ:
  • Асимптотический:
    • Оценка ресурсоемкости и времени выполнения (в частности, для рекурсивных алгоритмов);
    • Оценка роста потребности в ресурсах (например, времени выполнения) с увеличением объема данных.
  • Практический:
    • Получение «явных» функции трудоемкости;
    • Интервальный анализ функций;
    • Поиск критериев качества;
    • Методика рационального выбора.

теория автоматов

Грамматика	Языки	Автомат	Правила производства (ограничения)
Тип-0	Рекурсивно перечислимый	Машина Тьюринга	(нет ограничений)
Тип 1	Контекстно-зависимый	Линейно-ограниченная недетерминированная машина Тьюринга
Тип-2	Без контекста	Недетерминированные магазинный автомат
Тип-3	Обычный	Конечный автомат	а также

Теория автоматов - это изучение абстрактных машин (или, точнее, абстрактных «математических» машин или систем) и вычислительных задач, которые могут быть решены с помощью этих машин. Об этом говорит сайт https://intellect.icu . Эти абстрактные машины называются автоматами. Автоматы происходят от греческого слова (Αυτόματα), которое означает, что что-то делает что-то само по себе. Теория автоматов также тесно связана с теорией формального языка , поскольку автоматы часто классифицируются по классу формальных языков, которые они могут распознать. Автомат может быть конечным представлением формального языка, который может быть бесконечным множеством. Автоматы используются в качестве теоретических моделей вычислительных машин и используются для доказательства вычислимости.

Теория формального языка

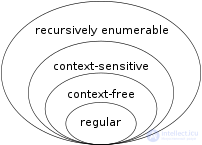
Набор включений, описываемых иерархией Хомского

Теория языков - это раздел математики, связанный с описанием языков как набора операций над алфавитом . Он тесно связан с теорией автоматов, поскольку автоматы используются для создания и распознавания формальных языков. Есть несколько классов формальных языков, каждый из которых позволяет более сложной спецификации языка , чем до него, т.е. Хомский иерархии , , и каждый из них соответствует классу автоматов, признающей его. Поскольку автоматы используются в качестве моделей для вычислений, формальные языки являются предпочтительным способом спецификации для любой проблемы, которая должна быть вычислена.

Современное состояние теории алгоритмов

В настоящее время теория алгоритмов развивается, главным образом, по трем направлениям.

• Классическая теория алгоритмов изучает проблемы формулировки задач в терминах формальных языков, вводит понятие задачи разрешения, проводит классификацию задач по классам сложности (P, NP и др.).

• Теория асимптотического анализа алгоритмов рассматривает методы получения асимптотических оценок ресурсоемкости или времени выполнения алгоритмов, в частности, для рекурсивных алгоритмов. Асимптотический анализ позволяет оценить рост потребности алгоритма в ресурсах (например, времени выполнения) с увеличением объема входных данных.

• Теория практического анализа вычислительных алгоритмов решает задачи получения явных функции трудоемкости, интервального анализа функций, поиска практических критериев качества алгоритмов, разработки методики выбора рациональных алгоритмов.

Анализ трудоемкости алгоритмов

Целью анализа трудоемкости алгоритмов является нахождение оптимального алгоритма для решения данной задачи. В качестве критерия оптимальности алгоритма выбирается трудоемкость алгоритма, понимаемая как количество элементарных операций, которые необходимо выполнить для решения задачи с помощью данного алгоритма. Функцией трудоемкости называется отношение, связывающие входные данные алгоритма с количеством элементарных операций.

Трудоемкость алгоритмов по-разному зависит от входных данных. Для некоторых алгоритмов трудоемкость зависит только от объема данных, для других алгоритмов — от значений данных, в некоторых случаях порядок поступления данных может влиять на трудоемкость. Трудоемкость многих алгоритмов может в той или иной мере зависеть от всех перечисленных выше факторов.

Одним из упрощенных видов анализа, используемых на практике, является асимптотический анализ алгоритмов. Целью асимптотического анализа является сравнение затрат времени и других ресурсов различными алгоритмами, предназначенными для решения одной и той же задачи, при больших объемах входных данных. Используемая в асимптотическом анализе оценка функции трудоемкости, называемая сложностью алгоритма, позволяет определить, как быстро растет трудоемкость алгоритма с увеличением объема данных. В асимптотическом анализе алгоритмов используются обозначения, принятые в математическом асимптотическом анализе. Ниже перечислены основные оценки сложности.

Основной оценкой функции сложности алгоритма f(n) является оценка 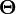. Здесь n — величина объема данных или длина входа. Мы говорим, что оценка сложности алгоритма

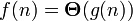
если при g > 0 при n > 0 существуют положительные с1, с2, n0, такие, что:

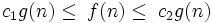
при n > n0, иначе говоря, можно найти такие с1 и c2, что при достаточно больших n f(n) будет заключена между

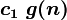и .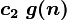

В таком случае говорят еще, что функция g(n) является асимптотически точной оценкой функции f(n), так как по определению функция f(n) не отличается от функции g(n) с точностью до постоянного множителя (см. асимптотическое равенство). Например, для метода сортировки heapsort оценка трудоемкости составляет

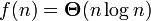то есть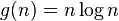

Из 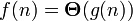следует, что .

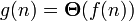Важно понимать, что 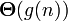представляет собой не функцию, а множество функций, описывающих рост 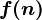с точностью до постоянного множителя.

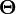дает одновременно верхнюю и нижнюю оценки роста функции. Часто бывает необходимо рассматривать эти оценки по отдельности. Оценка 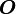представляет собой верхнюю асимптотическую оценку трудоемкости алгоритма. Мы говорим, что 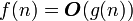если

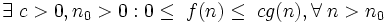
Иначе говоря, запись 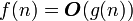означает, что f(n) принадлежит классу функций, которые растут не быстрее, чем функция g(n) с точностью до постоянного множителя.

Оценка 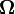задает нижнюю асимптотическую оценку роста функции f(n) и определяет класс функций, которые растут не медленнее, чем g(n) с точностью до постоянного множителя. 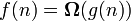если

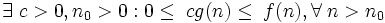
Например, запись обозначает класс функций, которые растут не медленнее, чем 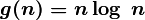, в этот класс попадают все полиномы со степенью большей единицы, равно как и все степенные функции с основанием большим единицы. Равенство 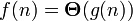выполняется тогда и только тогда, когда 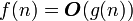и .

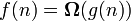Асимптотический анализ алгоритмов имеет не только практическое, но и теоретическое значение. Так, например, доказано, что все алгоритмы сортировки, основанные на попарном сравнении элементов, отсортируют n элементов за время, не меньшее .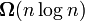

Важную роль в развитии асимптотического анализа алгоритмов сыграли A. Ахо, Дж. Ульман, Дж. Хопкрофт.

теория вычислимости

Теория вычислимости в первую очередь занимается вопросом о том, в какой степени проблема решаема на компьютере. Утверждение о том, что проблема остановки не может быть решена с помощью машины Тьюринга , является одним из наиболее важных результатов в теории вычислимости, поскольку это пример конкретной проблемы, которую легко сформулировать и которую невозможно решить с помощью машины Тьюринга. . Большая часть теории вычислимости основывается на результате проблемы остановки.

Другим важным шагом в теории вычислимости была теорема Райса , в которой говорится, что для всех нетривиальных свойств частичных функций непонятно , вычисляет ли машина Тьюринга частичную функцию с этим свойством.

Теория вычислимости тесно связана с разделом математической логики, называемым теорией рекурсии , которая снимает ограничение на изучение только моделей вычислений, которые сводятся к модели Тьюринга. Многие математики и теоретики вычислений, изучающие теорию рекурсии, будут называть ее теорией вычислимости.

Теория вычислительной сложности

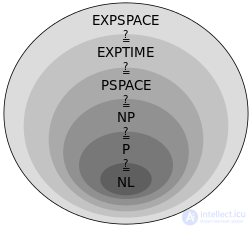
Представление отношения между классами сложности

теория сложности учитывает не только то, можно ли вообще решить проблему на компьютере, но и то, насколько эффективно проблема может быть решена. Рассмотрены два основных аспекта: временная сложность и пространственная сложность, которые, соответственно, показывают, сколько шагов требуется для выполнения вычисления и сколько памяти требуется для выполнения этого вычисления.

Чтобы проанализировать, сколько времени и пространства требуется для данного алгоритма , компьютерщики выражают время или пространство, необходимое для решения проблемы, как функцию размера входной задачи. Например, найти конкретное число в длинном списке чисел становится труднее, когда список чисел становится больше. Если мы говорим, что в списке n чисел, то, если список не отсортирован или не проиндексирован, нам, возможно, придется просмотреть каждое число, чтобы найти число, которое мы ищем. Таким образом, мы говорим, что для решения этой проблемы компьютер должен выполнить ряд шагов, которые линейно растут по размеру проблемы.

Чтобы упростить эту проблему, специалисты по информатике приняли нотацию Big O , которая позволяет сравнивать функции таким образом, чтобы не учитывать отдельные аспекты конструкции машины, а рассматривать только асимптотическое поведение по мере того, как проблемы становятся большими. Итак, в нашем предыдущем примере мы можем сказать, что проблема требует шаги для решения.

Возможно, самая важная открытая проблема во всей информатике - это вопрос о том, можно ли эффективно решить определенный широкий класс задач, обозначенных как NP . Это обсуждается далее в классах сложности P и NP , и проблема P в сравнении с NP является одной из семи задач Премии тысячелетия, поставленных Институтом математики Клея в 2000 году. Официальное описание проблемы было дано обладателем премии Тьюринга Стивеном Куком .

классы сложности

В рамках классической теории осуществляется классификация задач по классам сложности (P-сложные, NP-сложные, экспоненциально сложные и др.).

К классу P относятся задачи, которые могут быть решены за время, полиномиально зависящее от объема исходных данных, с помощью детерминированной вычислительной машины (например, машины Тьюринга),

а к классу NP — задачи, которые могут быть решены за полиномиально выраженное время с помощью недетерминированной вычислительной машины, то есть машины, следующее состояние которой не всегда однозначно определяется предыдущими. Работу такой машины можно представить как разветвляющийся на каждой неоднозначности процесс: задача считается решенной, если хотя бы одна ветвь процесса пришла к ответу. Другое определение класса NP: к классу NP относятся задачи, решение которых с помощью дополнительной информации полиномиальной длины, данной нам свыше, мы можем проверить за полиномиальное время. В частности, к классу NP относятся все задачи, решение которых можно проверить за полиномиальное время. Класс P содержится в классе NP. Классическим примером NP-задачи является задача о коммивояжере.

Поскольку класс P содержится в классе NP, принадлежность той или иной задачи к классу NP зачастую отражает наше текущее представление о способах решения данной задачи и носит неокончательный характер. В общем случае нет оснований полагать, что для той или иной NP-задачи не может быть найдено P-решение. Вопрос о возможной эквивалентности классов P и NP (то есть о возможности нахождения P-решения для любой NP-задачи) считается многими одним из основных вопросов современной теории сложности алгоритмов. Ответ на этот вопрос не найден до сих пор. Сама постановка вопроса об эквивалентности классов P и NP возможна благодаря введению понятия NP-полных задач. NP-полные задачи составляют подмножество NP-задач и отличаются тем свойством, что все NP-задачи могут быть тем или иным способом сведены к ним. Из этого следует, что если для NP-полной задачи будет найдено P-решение, то P-решение будет найдено для всех задач класса NP. Примером NP-полной задачи является задача о конъюнктивной форме

Исследования сложности алгоритмов позволили по-новому взглянуть на решение многих классических математических задач и найти для ряда таких задач (умножение многочленов и матриц, решение линейных систем уравнений и др.) решения, требующие меньше ресурсов, нежели традиционные.

Математические приложения теории алгоритмов

1. Исследование массовых проблем.
2. Приложения к основаниям математики: конструктивная семантика.
3. Приложения к математической логике: анализ формализованных языков логики и арифметики.
4. Вычислимый анализ.
5. Нумерованные структуры.
6. Приложения к теории вероятностей: определения случайной последовательности.
7. Приложения к теории информации: алгоритмический подход к понятию количества информации.
8. Оценки сложностей решения отдельных задач.
9. Влияние теории алгоритмов на алгоритмическую практику.

Литература

• Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ . INTRODUCTION TO ALGORITHMS. — 2-е изд. —М.: Вильямс, 2006. — С. 1296.
• Дональд Кнут Искусство программирования, том 1. Основные алгоритмы . The Art of Computer Programming, vol.1. Fundamental Algorithms. — 3-е изд. — М.: Вильямс, 2006. — С. 720.
• Колмогоров А. Н. Теория информации и теория алгоритмов. — М.: Наука, 1987. — 304 с.
• Марков А. А., Нагорный Н. М. Теория алгорифмов, изд. 2. — М.: ФАЗИС, 1996.

Вау!! 😲 Ты еще не читал? Это зря!

• Алгоритм
• Список основных разделов теории алгоритмов
• Неполнота математики
• Модель вычислений
• Стратегия вычислений
• Семантика ( программирование )
• Лямбда-исчисление
• Лямбда-исчисление с типами
• Комбинаторная логика
• Аппликативные вычислительные системы
• Категориальная абстрактная машина
• Суперкомбинаторы

• Теория алгоритмов
• Миниэнциклопедия по теории сложности и комбинаторным алгоритмам
• Лекции по теории сложности и комбинаторным алгоритмам

Надеюсь, эта статья про теория алгоритмов, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое теория алгоритмов, алгоритм, классы сложности , класс сложности , теория вычислимости , теория сложности, теория автоматов , класс сложности p , класс сложности np и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов