Лекция
Сразу хочу сказать, что здесь никакой воды про сложность алгоритмов, и только нужная информация. Для того чтобы лучше понимать что такое сложность алгоритмов, оценка сложности алгоритмов, анализ сложности алгоритмов, большое o, доминирующий оператор, о большое, big o, рекурсивная сложность, логарифмическая сложность, сложность рекурсивных алгоритмов, функции оценки сложности, практическая оценка сложности алгоритмов , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
Вы действительно понимаете что такое о большое (Big O)? Если это так, то эта статья поможет вам освежить ваши знания перед собеседованием. Если нет, эта статья расскажет вам о том что это такое и зачем нужно об этом знать.
Нотация О большое является одним из самых фундаментальных инструментов анализа сложности алгоритма. Эта статья написана с предположением, что вы уже являетесь программистом и за вашими плечами большое количество написанного кода. Кроме того, для лучшего понимания материала потребуется знания основ математики средней школы. И так если вы готовы, давайте начнем!
А размера n:
var M = A[ 0 ];
for ( var i = 0; i < n; ++i ) {
if ( A[ i ] >= M ) {
M = A[ i ];
}
}
if и else частями кода после вычисления if-условия) происходит мгновенно, и не будем учитывать эту инструкцию при подсчете. Для первой строки в коде выше:
var M = A[ 0 ];
A и для присвоения значения M (мы предполагаем, что n всегда как минимум 1). Эти две инструкции будут требоваться алгоритму, вне зависимости от величины n. Инициализация цикла for тоже будет происходить постоянно, что дает нам еще две команды: присвоение и сравнение.
i = 0;
i < n;
for. После каждой новой итерации мы будем иметь на две инструкции больше: инкремент i и сравнение для проверки, не пора ли нам останавливать цикл.
++i;
i < n;
4 + 2n — четыре на начало циклаfor и по две на каждую итерацию, которых мы имеем n штук. Теперь мы можем определить математическую функцию f(n) такую, что зная n, мы будем знать и необходимое алгоритму количество инструкций. Для цикла for с пустым телом f( n ) = 4 + 2n.
if ( A[ i ] >= M ) { ...
if может запускаться, а может и нет, в зависимости от актуального значения из массива. Если произойдет так, что A[ i ] >= M, то у нас запустятся две дополнительные команды: поиск в массиве и присваивание:
M = A[ i ]
f(n) так легко, потому что теперь количество инструкций зависит не только от n, но и от конкретных входных значений. Например, для A = [ 1, 2, 3, 4 ] программе потребуется больше команд, чем для A = [ 4, 3, 2, 1 ]. Когда мы анализируем алгоритмы, мы чаще всего рассматриваем наихудший сценарий. Каким он будет в нашем случае? Когда алгоритму потребуется больше всего инструкций до завершения? Ответ: когда массив упорядочен по возрастанию, как, например, A = [ 1, 2, 3, 4 ]. Тогда M будет переприсваиваться каждый раз, что даст наибольшее количество команд. Теоретики имеют для этого причудливое название — анализ наиболее неблагоприятного случая, который является ни чем иным, как просто рассмотрением максимально неудачного варианта. Таким образом, в наихудшем случае в теле цикла из нашего кода запускается четыре инструкции, и мы имеем f( n ) = 4 + 2n + 4n = 6n + 4.
f через «фильтр» для очищения ее от незначительных деталей, на которые теоретики предпочитают не обращать внимания.6n + 4 состоит из двух элементов: 6n и 4. При анализе сложности важность имеет только то, что происходит с функцией подсчета инструкций при значительном возрастании n. Это совпадает с предыдущей идеей «наихудшего сценария»: нам интересно поведение алгоритма, находящегося в «плохих условиях», когда он вынужден выполнять что-то трудное. Заметьте, что именно это по-настоящему полезно при сравнении алгоритмов. Если один из них побивает другой при большом входном потоке данных, то велика вероятность, что он останется быстрее и на легких, маленьких потоках. Вот почему мы отбрасываем те элементы функции, которые при росте n возрастают медленно, и оставляем только те, что растут сильно. Очевидно, что 4 останется 4 вне зависимости от значения n, а 6n наоборот будет расти. Поэтому первое, что мы сделаем, — это отбросим 4 и оставим только f( n ) = 6n.n. Так что наша функция превращается в f( n ) = n. Как вы можете заметить, это многое упрощает. Еще раз, константный множитель имеет смысл отбрасывать, если мы думаем о различиях во времени компиляции разных языков программирования. «Поиск в массиве» для одного ЯП может компилироваться совершенно иначе, чем для другого. Например, в Си выполнение A[ i ] не включает проверку того, что i не выходит за пределы объявленного размера массива, в то время как дляПаскаля она существует. Таким образом, данный паскалевский код:
M := A[ i ]
if ( i >= 0 && i < n ) {
M = A[ i ];
}
f( n ) = 2n + 8 оно будет описываться функцией f( n ) = n. Говоря языком математики, нас интересует предел функции f при n, стремящемся к бесконечности. Если вам не совсем понятно значение этой формальной фразы, то не переживайте — все, что нужно, вы уже знаете. (В сторону: строго говоря, в математической постановке мы не могли бы отбрасывать константы в пределе, но для целей теоретической информатики мы поступаем таким образом по причинам, описанным выше). Давайте проработаем пару задач, чтобы до конца вникнуть в эту концепцию.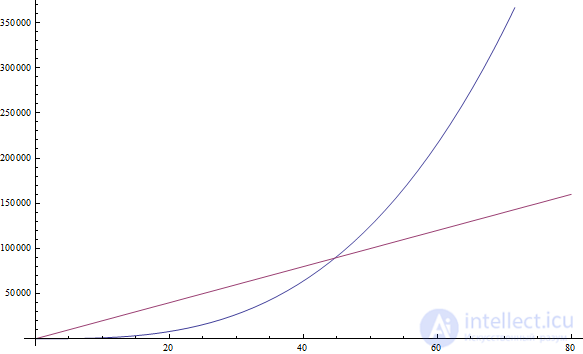
f( n ) = 5n + 12 даст f( n ) = n.f( n ) = 109 даст f( n ) = 1.109 * 1 , но 1 по-прежнему нужен, чтобы показать, что функция не равна нулюf( n ) = n2 + 3n + 112 даст f( n ) = n2n2 возрастает быстрее, чем 3n, который, в свою очередь, растет быстрее 112f( n ) = n3 + 1999n + 1337 даст f( n ) = n3n, мы по прежнему полагаем, что можем найти еще больший n, поэтому f( n ) = n3 все еще больше 1999n (см. рисунок выше)f( n ) = n + sqrt( n ) даст f( n ) = n n при увеличении аргумента растет быстрее, чем sqrt( n )n и посмотрите, какой из его членов имеет большую величину. Все очень просто, не так ли?f( n ) = 1, потому что в этом случае требуется константное число инструкций (конечно, при отсутствии рекурсии — см. далее). Одиночный цикл от 1 до n, дает асимптотику f( n ) = n, поскольку до и после цикла выполняет неизменное число команд, а постоянное же количество инструкций внутри цикла выполняется n раз.A размера n заданное значение:
f( n ) = n (что означает «линейный» более точно, мы рассмотрим в следующем разделе). Инструкция break позволяет программе завершиться раньше, даже после единственной итерации. Однако, напоминаю, что нас интересует самый неблагоприятный сценарий, при котором массив A вообще не содержит заданное значение. Поэтому f( n ) = n по-прежнему.
f( n ) = n.
v = a[ 0 ] + a[ 1 ]
f( n ) = 1.A размера n два одинаковых значения:
bool duplicate = false;
for ( int i = 0; i < n; ++i ) {
for ( int j = 0; j < n; ++j ) {
if ( i != j && A[ i ] == A[ j ] ) {
duplicate = true;
break;
}
}
if ( duplicate ) {
break;
}
}
f( n ) = n2.
n итераций дает f( n ) = n. Цикл внутри цикла — f( n ) = n2. Цикл внутри цикла внутри цикла — f( n ) = n3. И так далее.
int i;
for ( i = 0; i < n; ++i ) {
f( n );
}
f( n ) выполняет ровно n команд, то мы можем сказать, что количество инструкций во всей программе асимптотически приближается к n2, поскольку f( n ) вызывается n раз.
f, мы говорим, что наша программа — Θ( f( n ) ). Например, в примерах выше программы Θ( 1 ), Θ( n2 ) и Θ( n2 ), соответственно. Θ( n )произносится как «тета от n». Иногда мы говорим, что f( n ) (оригинальная функция подсчета инструкций, включая константы) есть Θ( что-то ). Например, можно сказать, что f( n ) = 2n — это функция, являющаяся Θ( n ). В общем, ничего нового. Можно так же написать, что 2n ∈ Θ( n ), что произносится: «два n принадлежит тета от n». Пусть вас не смущает такая нотация: она просто говорит о том, что если мы посчитаем количество необходимых программе команд, и оно будет равно 2n, то асимптотика этого алгоритма описывается как n (что мы находим, отбрасывая константу). Имея данную систему обозначений, приведем несколько истинных математических утверждений:
Θ( здесь )) временной сложностью, или просто сложностью нашего алгоритма.Таким образом, алгоритм с Θ( n ) имеет сложность n. Также существуют специальные названия для Θ( 1 ), Θ( n ), Θ( n2 ) и Θ( log( n ) ), потому что они встречаются очень часто. Говорят, что Θ( 1 ) — алгоритм с константным временем, Θ( n ) — линейный, Θ( n2 ) —квадратичный, а Θ( log( n ) ) — логарифмический (не беспокойтесь, если вы еще не знаете, что такое логарифм — скоро мы об этом поговорим).
Θ выполняются медленнее, чем с маленьким.
В реальной жизни иногда проблематично выяснить точно поведение алгоритма тем способом, который мы рассматривали выше. Особенно для более сложных примеров. Однако, мы можем сказать, что поведение нашего алгоритма никогда не пересечет некой границы. Это делает жизнь проще, так как четкого указания на то, насколько быстр наш алгоритм, у нас может и не появиться, даже при условии игнорирования констант (как раньше). Все, что нам нужно — найти эту границу, а как это сделать — проще объяснить на примере.
В конце статьи еще подробнее рассмотрим это понятие
Наиболее известной задачей, которую используют при обучении алгоритмам, является сортировка. Дается массив A размера n (звучит знакомо, не так ли?), и нас просят написать программу, его сортирующую. Интерес тут в том что, такая необходимость часто возникает в реальных системах. Например, обозревателю файлов нужно отсортировать файлы по имени, чтобы облегчить пользователю навигацию по ним. Или другой пример: в видео игре может возникнуть проблема сортировки 3D объектов, демонстрируемых на экране, по их расстоянию от точки зрения игрока в виртуальном мире, чтобы определить, какие из них будут для него видимы, а какие — нет (это называется Visibility Problem). Сортировка также интересна тем, что для нее существует множество алгоритмов, одни из которых хуже, чем другие. Так же эта задача проста для определения и объяснения. Поэтому давайте напишем кусок кода, который будет сортировать массив.
b = []
n.times do
m = a[ 0 ]
mi = 0
a.each_with_index do |element, i|
if element < m
m = element
mi = i
end
end
a.delete_at( mi )
b << m
end
a в коде выше. Минимум обозначен как m, а его индекс — как mi), который помещается в конец нового массива (b в нашем случае) и удаляется из оригинального. Затем среди оставшихся значений снова находится минимум, добавляется в новый массив (который теперь содержит два значения) и удаляется из старого. Процесс повторяется, пока все элементы не будут перенесены из первоначального в новый массив, что будет означать конец сортировки. В нашем примере мы имеем два вложенных цикла. Внешний цикл «пробегает» n раз, а внутренний — по разу для каждого элемента массива a. Поскольку изначально a имеет n элементов и на каждой итерации мы удаляем один из них, то сначала внутренний цикл «прокручивается» nраз, потом n - 1, n - 2 и так далее, пока на последней итерации внутренний цикл не пройдет всего один раз.1 + 2 + ... + (n - 1) + n, то найти сложность этого кода будет несколько проблематично. Но мы можем найти для нее «верхний предел». Для этого мы изменим программу (можно мысленно, не трогая код), чтобы сделать ее хуже, чем она есть, а затем выведем сложность для того, что получилось. Тогда можно будет уверенно сказать, что оригинальная программа работает или также плохо, или (скорее всего) лучше.n раз на каждой итерации. Некоторые из этих повторений буду бесполезны, но зато это поможет нам проанализировать сложность результирующего алгоритма. Если мы внесем это небольшое изменение, то наш новый алгоритм будет иметь Θ( n2), поскольку получим два вложенных цикла, каждый из которых выполняется ровно n раз. А если это так, то оригинальный алгоритм имеет O( n2 ). O( n2 ) произносится как «большое О от n в квадрате». Это говорит о том, что наша программа асимптотически не хуже, чем n2. Она будет работать или лучше, или также. Кстати, если код действительно имеет Θ( n2), то мы все еще говорим, что он O( n2 ). Чтобы лучше понять это, представьте, что изменение оригинальной программы меняет ее не сильно, делая лишь чуть-чуть хуже. Примерно как от добавления бесполезных инструкций в начало программы. Это изменит только константу в функции подсчета инструкций, которую мы проигнорируем в асимптотике. Таким образом, Θ( n2) для программы — это и O( n2 ) тоже.Θ( n ) также и O( n2 ) в дополнение к O( n ). Если мы представим, что Θ( n )программа — это просто цикл for, который выполняется n раз, мы можем сделать его хуже, добавив внутрь еще один for, тоже повторяющийсяn раз. Это даст программу с f( n ) = n2. Обобщая: любая программа с Θ( a ) является O( b ) при b худшем, чем a. Заметьте также, что изменение не обязательно должно иметь смысл или создавать код, аналогичный исходному. Все, что от него требуется — увеличить количество инструкций по отношению к заданному n. Мы используем результат для подсчета инструкций, а не для решения проблемы.O( n2 ), мы находимся в безопасности: анализ алгоритма показал, что он никогда не будет работать хуже, чем n2. Это дает нам хорошую оценку того, насколько быстра наша программа. Давайте прорешаем несколько примеров, чтобы вы получше освоились с новой нотацией.
Θ( n ) имеет O( n )Θ( n ) имеет O( n2 )Θ( n2 ) имеет O( n3 )Θ( n ) имеет O( 1 )O( 1 ) имеет Θ( 1 ) O( n ) имеет Θ( 1 )Θ( n ). Следовательно, O( n ) может быть достигнуто и без изменения программыn2 хуже n, то это истинаn3 хуже n2, то это истина1 не хуже n, то это ложь. Если программа асимптотически использует n инструкций (линейное число), то мы не можем сделать ее хуже так, чтобы асимптотически ей требовалась всего 1 (константное число) инструкций.Θ( 1 ), то он, безусловно, и O( n ). Но если он O( n ), то может и не быть Θ( 1 ). Например, Θ( n ) алгоритм является O( n ), а Θ( 1 ) — нет.O( n2 ), но так же и Θ( n2 ). Если вы не знаете, что такое арифметическая прогрессия, то посмотрите в википедии — это не сложно.О-сложность алгоритма представляет собой верхний предел его настоящей сложности, которую, в свою очередь, отображает Θ, то иногда мы говорим, что Θ дает нам точную оценку. Если мы знаем, что найденная нами граница не точна, то можем использовать строчное о, чтобы ее обозначить. Например, если алгоритм является Θ( n ), то его точная сложность — n. Следовательно, этот алгоритм O( n ) и O( n2 )одновременно. Поскольку алгоритм Θ( n ), то O( n ) определяет границу более точно. А O( n2 ) мы можем записать как о( n2 )(произносится: «маленькое o от n в квадрате»), чтобы показать, что мы знаем о нестрогости границы. Конечно, лучше, когда мы можем найти точные границы для нашего алгоритма, чтобы иметь больше информации о его поведении, но, к сожалению, это не всегда легко сделать.
Θ( n ) алгоритм, для которого мы нашли O( n ), как верхнюю границуΘ( n2 ) алгоритм, для которого мы нашли O( n3 ), как верхнюю границуΘ( 1 ) алгоритм, для которого мы нашли O( n ), как верхнюю границуΘ( n ) алгоритм, для которого мы нашли O( 1 ), как верхнюю границуΘ( n ) алгоритм, для которого мы нашли O( 2n ), как верхнюю границуΘ-сложность и O-сложность одинаковые, поэтому границапродолжение следует...
Часть 1 Анализ и оценка сложности алгоритмов, О большое, функции оценки сложности
Часть 2 Оптимальная сортировка - Анализ и оценка сложности алгоритмов, О большое,
Часть 3 Примеры - Анализ и оценка сложности алгоритмов, О большое, функции
Часть 4 Почему О большое может не имеет значения - Анализ и
А как ты думаешь, при улучшении сложность алгоритмов, будет лучше нам? Надеюсь, что теперь ты понял что такое сложность алгоритмов, оценка сложности алгоритмов, анализ сложности алгоритмов, большое o, доминирующий оператор, о большое, big o, рекурсивная сложность, логарифмическая сложность, сложность рекурсивных алгоритмов, функции оценки сложности, практическая оценка сложности алгоритмов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов