Оптимальная сортировка - Анализ и оценка сложности алгоритмов, О большое,

Логарифмы

Если вы знаете, что такое логарифмы, то можете спокойно пропустить этот раздел. Глава предназначается тем, кто незнаком с данным понятием или пользуется им настолько редко, что уже забыл что там к чему. Логарифмы важны, поскольку они очень часто встречаются при анализе сложности. Логарифм— это операция, которая при применении ее к числу делает его гораздо меньше (подобно взятию квадратного корня). Итак, первая вещь, которую вы должны запомнить: логарифм возвращает число, меньшее, чем оригинал. 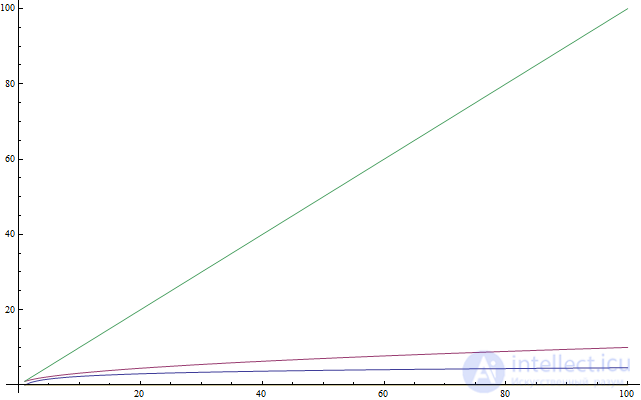На рисунке справа зеленый график — линейная функция f(n) = n, красный — f(n) = sqrt(n), а наименее быстро возрастающий — f(n) = log(n). Далее: подобно тому, как взятие квадратного корня является операцией, обратной возведению в квадрат, логарифм — обратная операция возведению чего-либо в степень.

Поясню на примере. Рассмотрим уравнение

2^x = 1024

Чтобы найти из него x, спросим себя: в какую степень надо возвести 2, чтобы получить 1024? Ответ: в десятую. В самом деле, 2¹⁰ = 1024, что легко проверить. Логарифмы помогают нам описать данную задачу, используя новую нотацию. В данном случае, 10 является логарифмом 1024 и записывается, как log( 1024 ). Читается: «логарифм 1024». Поскольку мы использовали 2 в качестве основания, то такие логарифмы называются «по основанию 2». Основанием может быть любое число, но в этой статье мы будем использовать только двойку. Если вы ученик-олимпиадник и не знакомы с логарифмами, то я рекомендую вам попрактиковаться после того, как закончите чтение этой статьи. В информатике логарифмы по основанию 2 распространены больше, чем какие-либо другие, поскольку часто мы имеем всего две сущности: 0 и 1. Также существует тенденция разбивать объемные задачи пополам, а половин, как известно, тоже бывает всего две. Поэтому для дальнейшего чтения статьи вам достаточно иметь представление только о логарифмах по основанию 2.

---

Практическая рекомендация: на соревнованиях алгоритмы часто реализуются на С++. Как только вы проанализировали сложность вашего алгоритма, так сразу можете получить и грубую оценку того, как быстро он будет работать, приняв, что в секунду выполняется 1 000 000 команд. Их количество считается из полученной вами функции асимптотической оценки, описывающей алгоритм. Например, вычисление по алгоритму с Θ( n ) займет около секунды при n = 1 000 000.

---

рекурсивная сложность

А теперь давайте обратимся к рекурсивным функциям. Рекурсивная функция — это функция, которая вызывает сама себя. Можем ли мы проанализировать ее сложность? Следующая функция, написанная на Python, вычисляет факториал заданного числа. Факториал целого положительного числа находится как произведение всех предыдущих положительных целых чисел. Например, факториал 5 — это 5 * 4 * 3 * 2 * 1. Обозначается он как «5!» и произносится «факториал пяти» (впрочем, некоторые предпочитают «ПЯТЬ!!!11»).

def factorial( n ):
    if n == 1:
        return 1
    return n * factorial( n - 1 )

Давайте проанализируем эту функцию. Она не содержит циклов, но ее сложность все равно не является константной. Что ж, придется вновь заняться подсчетом инструкций. Очевидно, что если мы применим эту функцию к некоторому n, то она будет вычисляться n раз. (Если вы в этом не уверены, то можете вручную расписать ход вычисления при n = 5, чтобы определить, как это на самом деле работает.) Таким образом, мы видим, что эта функция является Θ( n ).

Если вы все же не уверены в этом, то вы всегда можете найти точную сложность путем подсчета количества инструкций. Примените этот метод к данной функции, чтобы найти ее f( n ), и убедитесь, что она линейная (напомню, что линейность означает Θ( n )).

логарифмическая сложность

Одной из известнейших задач в информатике является поиск значения в массиве. Мы уже решали ее ранее для общего случая. Задача становится интереснее, если у нас есть отсортированный массив, в котором мы хотим найти заданное значение. Одним из способов сделать это является бинарный поиск. Мы берем средний элемент из нашего массива: если он совпадает с тем, что мы искали, то задача решена. В противном случае, если заданное значение больше этого элемента, то мы знаем, что оно должно лежать в правой части массива. А если меньше — то в левой. Мы будем разбивать эти подмассивы до тех пор, пока не получим искомое.

Вот реализация такого метода в псевдокоде:

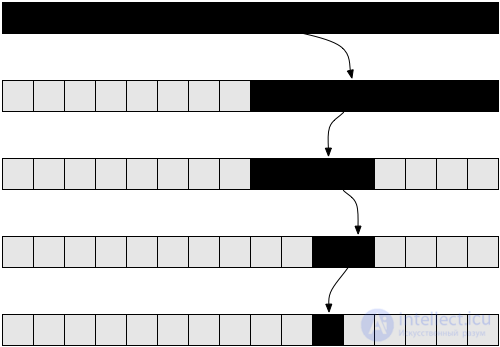
Приведенный псевдокод — упрощение настоящей реализации. На практике этот метод описать проще, чем воплотить, поскольку программисту нужно решить некоторые дополнительные вопросы. Например, защиту от ошибок на одну позицию (off-by-one error, OBOE), да и деление на два не всегда может давать целое число, поэтому потребуется применять функции floor() или ceil(). Однако, предположим, что в нашем случае деление всегда будет успешным, наш код защищен от ошибок off-by-one, и все, что мы хотим — это проанализировать сложность данного метода. Если вы никогда раньше не реализовывали бинарный поиск, то можете сделать это на вашем любимом языке программирования. Такая задача по-настоящему поучительна.

Если вы не уверены, что метод работает в принципе, то отвлекитесь и решите вручную какой-нибудь простой пример.

Теперь давайте попробуем проанализировать этот алгоритм. Еще раз, в этом случае мы имеем рекурсивный алгоритм. Давайте для простоты предположим, что массив всегда разбивается ровно пополам, игнорируя +1 и -1 части в рекурсивном вызове. К этому моменту вы должны быть уверены, что такое небольшое изменение, как игнорирование +1 и -1, не повлияет на конечный результат оценки сложности. В принципе, обычно этот факт необходимо доказывать, если мы хотим проявить осторожность с математической точки зрения. Но на практике это очевидно на уровне интуиции. Также для простоты давайте предположим, что наш массив имеет размер одной из степеней двойки. Опять-таки, это предположение никоим образом не повлияет на конечный результат расчета сложности алгоритма. Наихудшим сценарием для данной задачи будет вариант, когда массив в принципе не содержит искомое значение. В этом случае мы начинаем с массива размером n на первом рекурсивном вызове, n / 2 на втором, n / 4 на третьем и так далее. В общем, наш массив разбивается пополам на каждом вызове до тех пор, пока мы не достигнем единицы. Давайте запишем количество элементов в массиве на каждом вызове:
0-я итерация: n
1-я итерация: n / 2
2-я итерация: n / 4
3-я итерация: n / 8
…
i-я итерация: n / 2ⁱ
…
последняя итерация: 1

Заметьте, что на i-й итерации массив имеет n / 2ⁱ элементов. Мы каждый раз разбиваем его пополам, что подразумевает деление количества элементов на два (равноценно умножению знаменателя на два). Проделав это i раз, получим n / 2ⁱ. Процесс будет продолжаться, и из каждого большого i мы будем получать меньшее количество элементов до тех пор, пока не достигнем единицы. Если мы захотим узнать, на какой итерации это произошло, нам нужно будет просто решить следующее уравнение:

1 = n / 2ⁱ

Равенство будет истинным только тогда, когда мы достигнем конечного вызова функции binarySearch(), так что узнав из него i, мы будем знать номер последней рекурсивной итерации. Умножив обе части на 2ⁱ, получим:

2ⁱ = n

Если вы прочли раздел о логарифмах выше, то такое выражение будет для вас знакомым. Решив его, мы получим:

i = log( n )

Этот ответ говорит нам, что количество итераций, необходимых для бинарного поиска, равняется log( n ), где n — размер оригинального массива.

Если немного подумать, то это имеет смысл. Например, возьмем n = 32 (массив из 32-х элементов). Сколько раз нам потребуется разделить его, чтобы получить один элемент? Считаем: 32 → 16 → 8 → 4 → 2 → 1 — итого 5 раз, что является логарифмом 32. Таким образом, сложность бинарного поиска равна Θ( log( n ) ).

Последний результат позволяет нам сравнивать бинарный поиск с линейным (нашим предыдущим методом). Несомненно, log( n ) намного меньше n, из чего правомерно заключить, что первый намного быстрее второго. Так что имеет смысл хранить массивы в отсортированном виде, если мы собираемся часто искать в них значения.

---

Практическая рекомендация: улучшение асимптотического времени выполнения программы часто чрезвычайно повышает ее производительность. Намного сильнее, чем небольшая «техническая» оптимизация в виде использования более быстрого языка программирования.

Оптимальная сортировка

Поздравляю! Теперь вы знаете о том, как анализировать сложность алгоритмов , что такое асимптотическая оценка и нотация «большое-О». Вы также в курсе, как интуитивно выяснить является ли сложностью алгоритма O( 1 ), O( log( n ) ), O( n ), O( n² ) и так далее. Вы знакомы с символами o, O, ω, Ω, Θ и понятием «наихудшего случая». Если вы добрались до этого места, то моя статья уже выполнила свою задачу.

Этот финальный раздел — опциональный. Он несколько сложнее, так что можете не стесняясь пропустить его, если хотите.От вас потребуется сфокусироваться и потратить некоторое время на решение упражнений. Однако, так же здесь будет продемонстрирован очень полезный и мощный способ анализа сложности алгоритмов, что, безусловно, стоит внимания.

Мы рассматривали реализацию сортировки, называемую сортировкой выбором, и упоминали, что она не является оптимальной. Оптимальный алгоритм — это тот, который решает задачу наилучшим образом, подразумевая, что не существует алгоритма, делающего это лучше. Т.е. все прочие алгоритмы для решения данной проблемы имеют такую же или большую сложность. Может существовать масса оптимальных алгоритмов, имеющих одинаковую сложность. Та же проблема сортировки может быть решена оптимально многими способами. Например, мы можем использовать для быстрой сортировки ту же идею, что и при бинарном поиске. Такой способ называется сортировкой слиянием.

Прежде, чем реализовать собственно сортировку слиянием, нам надо написать вспомогательную функцию. Назовем ее merge, и пусть она принимает два уже отсортированных массива и соединяет их в один (тоже отсортированный). Это легко сделать:

def merge( A, B ):
    if empty( A ):
        return B
    if empty( B ):
        return A
    if A[ 0 ] < B[ 0 ]:
        return concat( A[ 0 ], merge( A[ 1...A_n ], B ) )
    else:
        return concat( B[ 0 ], merge( A, B[ 1...B_n ] ) )

Функция concat принимает элемент («голову») и массив («хвост») и соединяет их, возвращая новый массив с «головой» в качестве первого элемента и «хвостом» в качестве оставшихся элементов. Например, concat( 3, [ 4, 5, 6 ] ) вернет [ 3, 4, 5, 6 ]. Мы используем A_n иB_n, чтобы обозначить размеры массивов A и B соответственно.

Анализ этого алгоритма показывает, что его время выполнения — Θ( n ), где n — длина результирующего массива (n = A_n + B_n).

Используя эту функцию, мы можем построить лучший алгоритм сортировки. Идея следующая: мы разбиваем массив на две части, рекурсивно сортируем каждую из них и объединяем два отсортированных массива в один. Псевдокод:

def mergeSort( A, n ):
    if n = 1:
        return A # it is already sorted
    middle = floor( n / 2 )
    leftHalf = A[ 1...middle ]
    rightHalf = A[ ( middle + 1 )...n ]
    return merge( mergeSort( leftHalf, middle ), mergeSort( rightHalf, n - middle ) )

Эта функция сложнее предыдущих для понимания, поэтому выполнение следующего упражнения может потребовать у вас больше времени.

В качестве финального упражнения давайте проанализируем сложность mergeSort. На каждом шаге мы разбиваем исходный массив на две равные части (аналогично binarySearch). Однако, в этом случае дальнейшие вычисления происходят на обеих частях. После возврата рекурсии мы применяем к результатам операцию merge, что занимает Θ( n ) времени.

Итак, мы разбили оригинальный массив на две части, размером n / 2 каждая. Когда мы будем их соединять, в операции будут участвовать nэлементов, следовательно, время выполнения будет Θ( n ). Рисунок ниже поясняет эту рекурсию: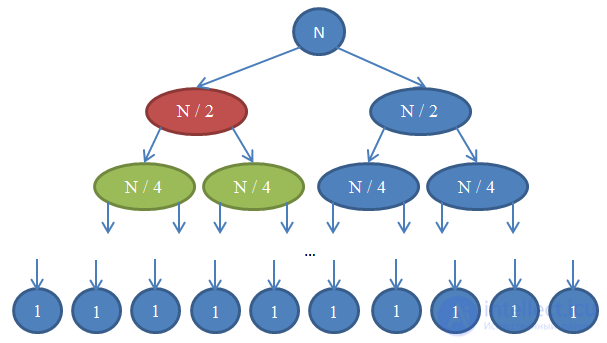



Давайте посмотрим, что здесь происходит. Каждый кружок представляет собой вызов функции mergeSort. Число в кружке показывает количество элементов в массиве, который будет отсортирован. Верхний синий кружок — первоначальный вызов mergeSort для массива, размером n. Стрелочки показывают рекурсивные вызовы между функциями. Оригинальный вызов mergeSort порождает два новых для массивов, размером n / 2 каждый. В свою очередь, каждый из них порождает еще два вызова с массивами в n / 4 элементов, и так далее до тех пор, пока мы не получим массив размера 1. Эта диаграмма называется рекурсивным деревом, потому что иллюстрирует работу рекурсии и выглядит как дерево (точнее, как инверсия дерева с корнем вверху и листьями внизу).

Заметьте, что количество элементов в каждой строке остается равным n. Так же обратите внимание, что каждый вызывающий узел использует для операции merge результаты, полученные от вызываемых узлов. Например, красный узел сортирует n / 2 элементов. Чтобы сделать это, он разбивает n / 2 массив на два по n / 4, рекурсивно вызывает с каждым из них mergeSort (зеленые узлы) и объединяет результаты в единое целое размером n / 2.

В результате сложностью каждой строки является Θ( n ). Мы знаем, что количество таких строк, называемое глубиной рекурсивного дерева, будет log( n ). Основанием для этого являются те же аргументы, которые мы использовали для бинарного поиска. Итак, у нас log( n ) строк со сложностью Θ( n ), следовательно, общая сложность mergeSort: Θ( n * log( n ) ). Это намного лучше, чем Θ( n² ), которую нам дает сортировка выбором (помните, log( n ) намного меньше n, поэтому n * log( n ) так же намного меньше n * n = n²).

Как вы видели в последнем примере, анализ сложности позволяет нам сравнивать алгоритмы, чтобы понять, который из них лучше. Исходя из этих соображений, теперь мы можем быть уверены, что для массивов больших размеров сортировка слиянием намного опередит сортировку выбором. Такое заключение было бы проблематично сделать, если бы мы не имели теоретического базиса анализа разработанных нами алгоритмов. Несомненно, алгоритмы сортировки с временем выполнения Θ( n * log( n ) ) широко используются на практике. Например, ядро Linux использует алгоритм, называемый «сортировкой кучей», который имеет такое же время выполнения, как и сортировка слиянием. Заметим, что мы не будем доказывать оптимальность данных алгоритмов сортировки. Это потребовало бы гораздо более громоздких математических аргументов, но будьте уверены: с точки зрения сложности нельзя найти вариант лучше.

После изучения данной статьи, приобретенная вами интуиция относительно анализа сложности алгоритмов должна будет помогать вам создавать быстрые программы и сосредотачивать усилия по оптимизации на тех вещах, которые действительно имеют большое влияние на скорость выполнения. Все вместе позволит вам работать более продуктивно. К тому же математический язык и нотации (например, «большое О»), рассмотренные в данной статье, будут вам полезны при общении с другими разработчиками программного обеспечения, когда речь зайдет о времени выполнения алгоритмов, и, надеюсь, вы сможете применить на практике приобретенные знания.