Лекция
Это продолжение увлекательной статьи про сложность алгоритмов.
...
По этой причине всегда необходимо проводить хотя бы поверхностный анализ объемной сложности рекурсивных процедур.
Оценка сложности алгоритма до порядка является верхней границей сложности алгоритмов. Если программа имеет большой порядок сложности, это вовсе не означает, что алгоритм будет выполняться действительно долго. На некоторых наборах данных выполнение алгоритма занимает намного меньше времени, чем можно предположить на основе их сложности. Например, рассмотрим код, который ищет заданный элемент в векторе A.
function Locate(data: integer): integer;
var
i: integer;
fl: boolean;
begin
fl:=false; i:=1;
while (not fl) and (i<=N) do
begin
if A[i]=data then
fl:=true
else
i:=i+1;
end;
if not fl then
i:=0;
Locate:=I;
end;
Если искомый элемент находится в конце списка, то программе придется выполнить N шагов. В таком случае сложность алгоритма составит O(N). В этом наихудшем случае время работы алгоритма будем максимальным.
С другой стороны, искомый элемент может находится в списке на первой позиции. Алгоритму придется сделать всего один шаг. Такой случай называется наилучшим и его сложность можно оценить, как O(1).
Оба эти случая маловероятны. Нас больше всего интересует ожидаемый вариант. Если элемента списка изначально беспорядочно смешаны, то искомый элемент может оказаться в любом месте списка. В среднем потребуется сделать N/2 сравнений, чтобы найти требуемый элемент. Значит сложность этого алгоритма в среднем составляет O(N/2)=O(N).
В данном случае средняя и ожидаемая сложность совпадают, но для многих алгоритмов наихудший случай сильно отличается от ожидаемого. Например, алгоритм быстрой сортировки в наихудшем случае имеет сложность порядка O(N^2), в то время как ожидаемое поведение описывается оценкой O(N*log(N)), что много быстрее.
Сложность алгоритмов обычно оценивают по времени выполнения или по используемой памяти. В обоих случаях сложность зависит от размеров входных данных: массив из 100 элементов будет обработан быстрее, чем аналогичный из 1000. При этом точное время мало кого интересует: оно зависит от процессора, типа данных, языка программирования и множества других параметров. Важна лишь асимптотическая сложность, т. е. сложность при стремлении размера входных данных к бесконечности.
Допустим, некоторому алгоритму нужно выполнить 8n3 + 7n условных операций, чтобы обработать n элементов входных данных. При увеличении n на итоговое время работы будет значительно больше влиять возведение n в куб, чем умножение его на 8 или же прибавление 7n. Тогда говорят, что временная сложность этого алгоритма равна О(n3), т. е. зависит от размера входных данных кубически.
Использование заглавной буквы О (или так называемая О-нотация) пришло из математики, где ее применяют для сравнения асимптотического поведения функций. Формально O(f(n)) означает, что время работы алгоритма (или объем занимаемой памяти) растет в зависимости от объема входных данных не быстрее, чем некоторая константа, умноженная на f(n).
Такой сложностью обладает, например, алгоритм поиска наибольшего элемента в не отсортированном массиве. Нам придется пройтись по всем n элементам массива, чтобы понять, какой из них максимальный.
Простейший пример — бинарный поиск. Если массив отсортирован, мы можем проверить, есть ли в нем какое-то конкретное значение, методом деления пополам. Проверим средний элемент, если он больше искомого, то отбросим вторую половину массива — там его точно нет. Если же меньше, то наоборот — отбросим начальную половину. И так будем продолжать делить пополам, в итоге проверим log n элементов.
Такую сложность имеет, например, алгоритм сортировки вставками. В канонической реализации он представляет из себя два вложенных цикла: один, чтобы проходить по всему массиву, а второй, чтобы находить место очередному элементу в уже отсортированной части. Таким образом, количество операций будет зависеть от размера массива как n * n, т. е. n2.
Бывают и другие оценки по сложности, но все они основаны на том же принципе.
Также случается, что время работы алгоритма вообще не зависит от размера входных данных. Тогда сложность обозначают как O(1). Например, для определения значения третьего элемента массива не нужно ни запоминать элементы, ни проходить по ним сколько-то раз. Всегда нужно просто дождаться в потоке входных данных третий элемент и это будет результатом, на вычисление которого для любого количества данных нужно одно и то же время.
Аналогично проводят оценку и по памяти, когда это важно. Однако алгоритмы могут использовать значительно больше памяти при увеличении размера входных данных, чем другие, но зато работать быстрее. И наоборот. Это помогает выбирать оптимальные пути решения задач исходя из текущих условий и требований.
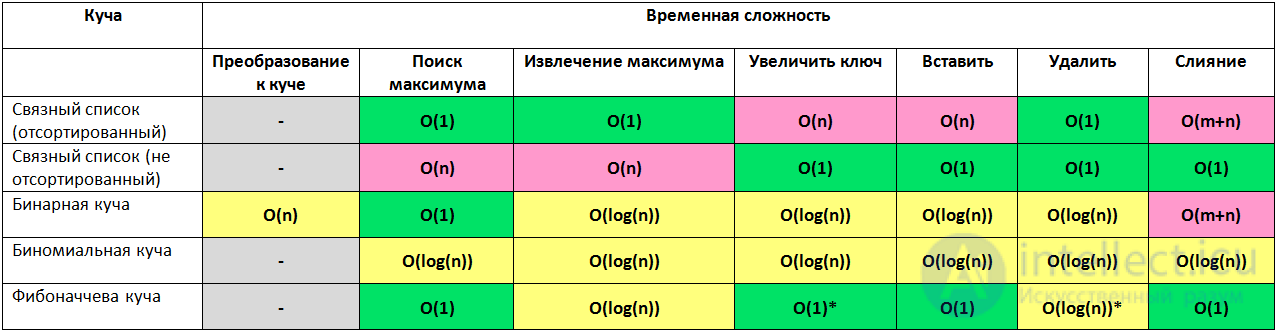
Время выполнения алгоритма с определенной сложностью в зависимости от размера входных данных при скорости 106 операций в секунду:
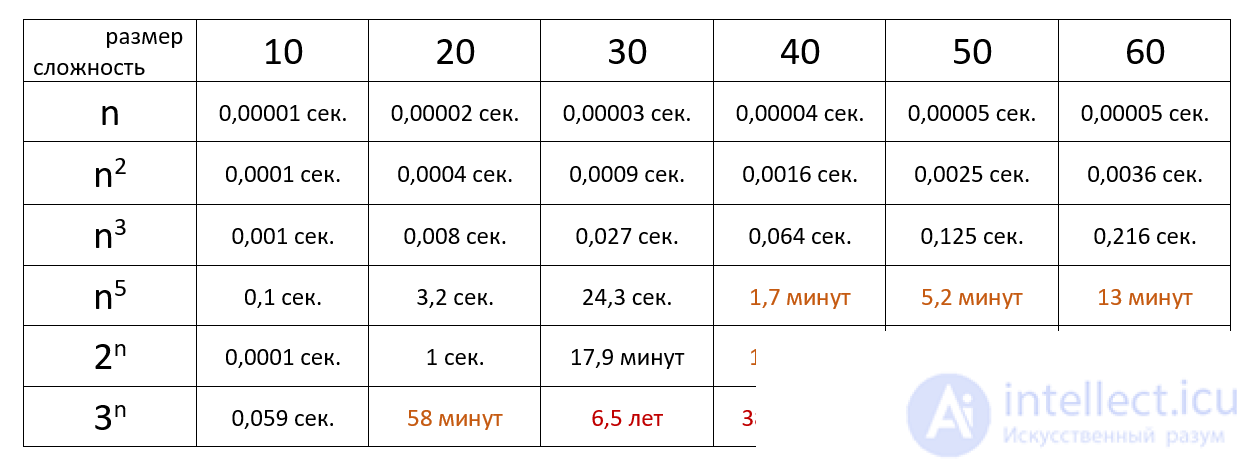
Таким образом при запуске алгоритма с разными наборами и обемами данных можно асимтотически построить графики и определить О большое или о маленькое

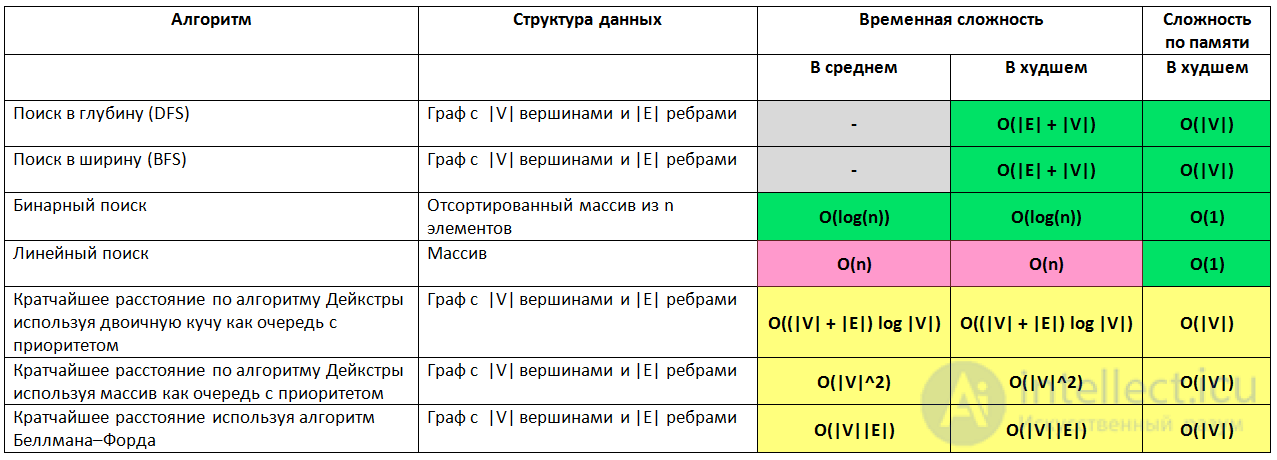

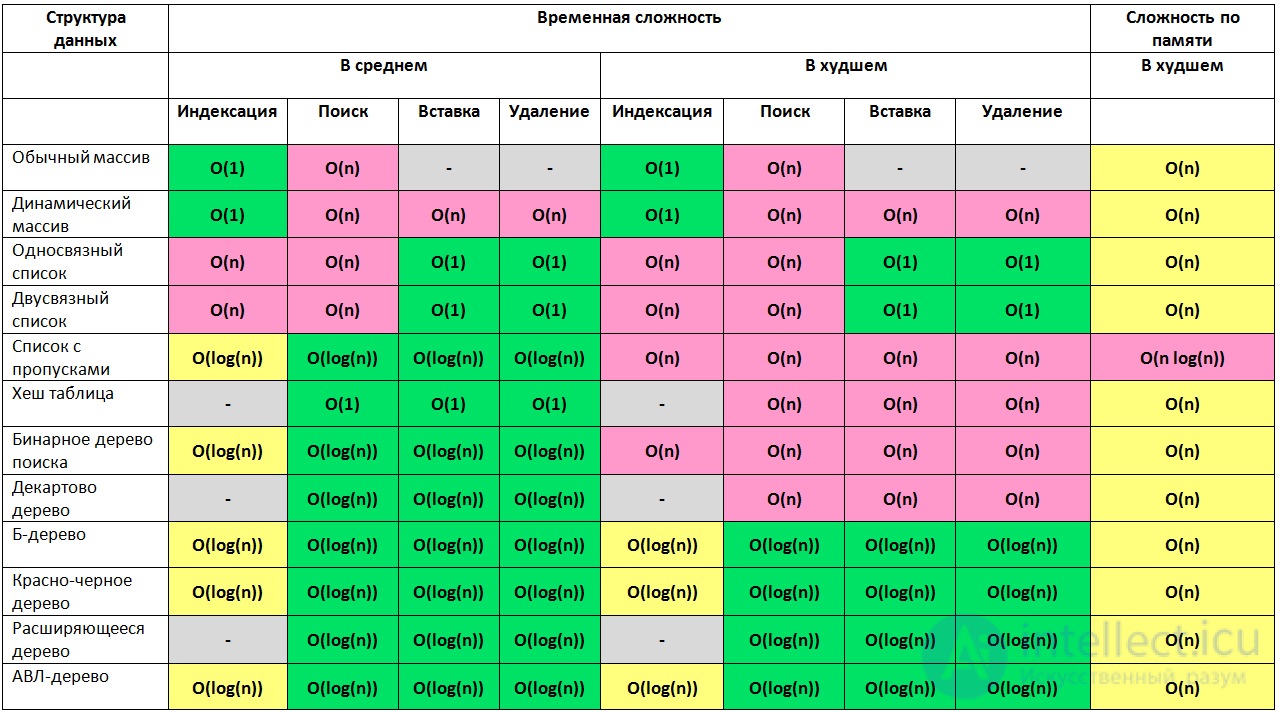



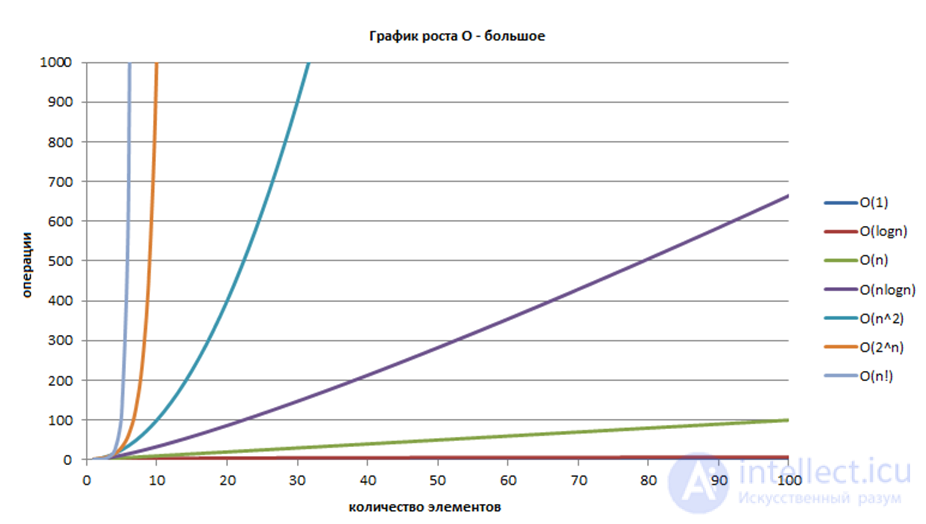
«Нотация О большое — это математическая нотация, которая описывает ограничивающее поведение функции, когда аргумент стремится к определенному значению или бесконечности. Он является членом семейства нотаций, изобретенных Полом Бахманом, Эдмундом Ландау и другими, которые в совокупности называются нотациями Бахмана-Ландау или асимптотическими нотациями ».
Проще говоря, нотация О большое описывает сложность вашего кода с использованием алгебраических терминов.
Чтобы понять, что такое О большое, мы можем взглянуть на типичный пример O (n²), который обычно произносится как «Большой O в квадрате». Буква «n» здесь представляет размер входных данных, а функция «g (n) = n²» внутри «O ()» дает нам представление о том, насколько сложен алгоритм по отношению к количеству входных данных.
Типичным алгоритмом со сложностью O(n²) будет алгоритм сортировки выбором. Сортировка выбором — это алгоритм сортировки, который выполняет итерацию по списку, чтобы гарантировать, что каждый элемент с индексом i является i-м наименьшим/наибольшим элементом списка. Наглядный пример.
https://www.youtube.com/embed/Ns4TPTC8whwАлгоритм может быть описан следующим кодом. Чтобы убедиться, что i-й элемент является i-м наименьшим элементом в списке, этот алгоритм сначала просматривает список с помощью цикла for. Затем для каждого элемента он использует другой цикл for, чтобы найти наименьший элемент в оставшейся части списка.
В этом сценарии мы рассматриваем переменную List как входные данные, поэтому размер ввода n — это количество элементов внутри List. Предположим, что оператор if, а присвоение значения, ограниченное оператором if, занимает постоянное время. Затем мы можем найти О большое для функции SelectionSort, проанализировав, сколько раз выполняются операторы.
Сначала внутренний цикл for выполняет операторы внутри n раз. А затем, после увеличения i, внутренний цикл for выполняется n-1 раз … пока он не будет запущен еще один раз, тогда оба цикла for достигнут своих условий завершения.
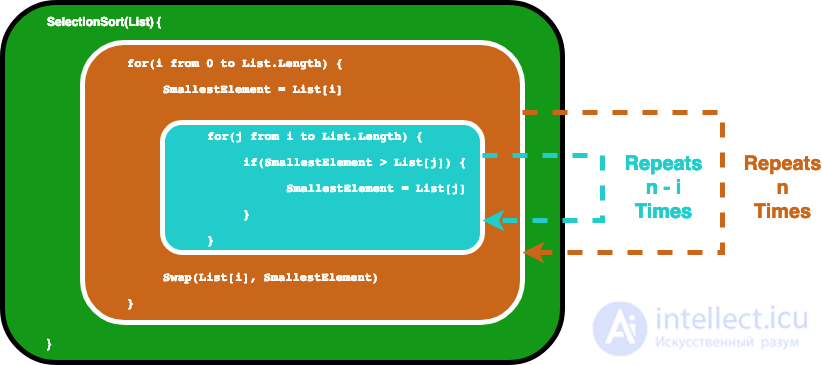
Selection Sort Loops Illustrated
На самом деле это в конечном итоге дает нам геометрическую сумму, и благодаря математики средней школе мы обнаружим, что внутренний цикл будет повторяться 1 + 2… + n раз, что равно n(n-1)/2 раза. Если мы умножим это, мы получим n²/2-n/2.
Когда мы вычисляем О большое, мы заботимся только о доминирующих операторах, и не заботимся о коэффициентах. Таким образом, мы выбираем n² как О большое. Мы записываем его как O(n²), а произносим как «О большое в квадрате».
Теперь вам может быть интересно, что это за «доминирующие операторы»? И почему нас не волнуют коэффициенты? Не волнуйтесь, мы рассмотрим эти вопросы по очереди далее.
Когда-то давно жил один индийский король, который захотел наградить мудреца. Мудрец попросил в качестве награды только пшеницы, которая бы заполнила все шахматную доску.
Но с определенным условием: в первой клетке должно быть 1 зернышко пшеницы, затем 2 зернышка на второй клетке, затем 4 на следующей … и так далее на каждой клетке шахматной доске должно быть вдвое больше количество зерен, чем на предыдущей. Наивный король согласился без колебаний, думая, что это слишком простое условие…

Wheat and Chess Board, Image from Wikipedia
Так сколько зерна пшеницы должен царь мудрецу? Мы знаем, что шахматная доска имеет 8 квадратов на 8 квадратов, что в сумме составляет 64 фишки, поэтому в итоговой фишке должно быть 2⁶⁴ зерна пшеницы. Если вы проведете самостоятельный расчет, вы получите 1,8446744 * 10¹⁹, то есть около 18, за которыми следуют 18 нулей. Предполагая, что каждое зерно пшеницы весит 0,01 грамма, это дает нам 184 467 440 737 тонн пшеницы. А 184 миллиарда тонн — это много, не правда ли?
Числа могут расти довольно быстро, не так ли? Та же логика относится и к компьютерным алгоритмам. Если требуемые усилия для выполнения задачи растут экспоненциально по отношению к размеру входных данных, алгоритм может в конечном итоге стать чрезвычайно затратным.
Если вы продолжите удвоение 2⁶⁴, то результат будет быстро потерян за пределами значащих цифр. Вот почему, когда мы смотрим на темпы роста, мы заботимся только о доминирующих операторах. И поскольку мы хотим проанализировать рост по отношению к размеру ввода, коэффициенты, которые только умножают число, и не растут с размером ввода, не содержат никакой полезной информации.
Ниже приведено формальное определение Большого O:

CSE 373 Slides from University of Washington
Формальное определение полезно, когда вам нужно выполнить математическое доказательство. Например, сложность для сортировки выбором может быть определена функцией f (n) = n²/2-n/2, как мы обсуждали в предыдущем разделе.
Если мы допустим, чтобы наша функция g(n) была n², мы можем найти константу c = 1 и N₀ = 0, при условии, N > N₀, где N² всегда будет больше, чем N²/2-N/2. Мы можем легко доказать это, вычитая N²/2 из обеих функций, тогда мы можем видеть, что N²/2 > -N/2 будет истинно, когда N>0. Поэтому мы можем прийти к выводу, что f(n) = O (n²), в другом порядке выбора это «О большое квадрат».
Вы могли заметить небольшую хитрость. То есть, если вы заставите g(n) расти быстрее, чем что-либо другое, O(g(n)) всегда будет достаточно большим. Например, для любой полиномиальной функции вы всегда будете правы, говоря, что оно являются O(2ⁿ), потому что 2ⁿ в конечном итоге будет всегда больше любого полинома.
С математической точки зрения вы будете правы, но обычно, когда мы говорим о Большом O, нам нужно знать жесткую границу (tight bound) функции. Вы узнаете об этом больше, в следующем раздел.
Но прежде чем мы пойдем дальше, давайте проверим ваше понимание следующим вопросом. Ответ будет приведен в следующем разделе.
Вопрос: Допустим изображение представлено двумерным массивом пикселей. Вы используете вложенный цикл for для итерации по каждому пикселю (то есть у вас есть цикл for, проходящий по всем столбцам, и другой цикл внутри, чтобы пройти по всем строкам). Какая в этом случае будет сложность алгоритма?
Ниже приведены формальные математические определения этих нотаций:
О большое: «f(n) есть O(g (n))» тогда и только тогда, когда некоторые константы c и N₀, f(N) ≤ cg(N) для всех N> N₀
Малое O: «f(n) есть o (g(n))», если f(n) есть O(g(n)) и f(n) не есть Θ(g(n))
Омега: «f(n) есть Ω(g(n))» тогда и только тогда, когда некоторые константы c и N₀, f(N) ≥ cg(N) для всех N> N₀
Тета: «f (n) есть Θ(g (n))» тогда и только тогда, когда f(n) есть O(g(n)), а f(n) есть Ω(g(n))
Простыми словами:
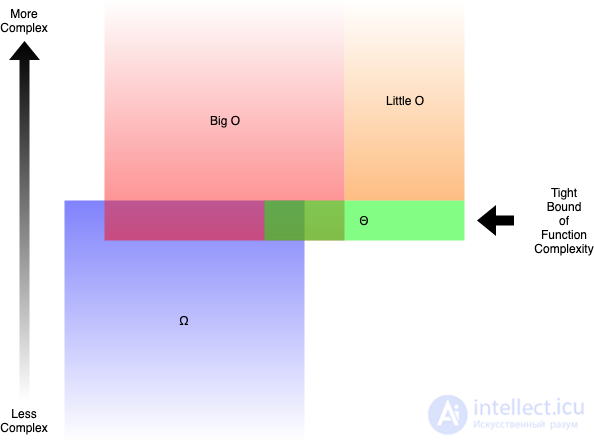
Relationships between Big O, Little O, Omega & Theta Illustrated
Например, функция g(n) = n² + 3n — это O(n³), o(n⁴), Θ(n²) и Ω (n). Но вы все равно были бы правы, если бы сказали, что это Ω(n²) или O(n²).
Вообще, когда мы говорим о Большом O, мы на самом деле имеем в виду Тета (Θ Theta). Бессмысленно, когда вы определяете верхнюю границу, намного превышающую объем анализа. Это было бы похоже на решение неравенств путем помещения ∞ на большую сторону, что почти всегда формально сделает вас правым.
Но как определить, какие функции сложнее других?
Когда мы пытаемся выяснить О большое для конкретной функции g(n), мы заботимся только о доминирующем операторе (dominant term) функции. доминирующий оператор — это такой оператор, который растет быстрее всего.
Например, n² растет быстрее, чем n, поэтому, если у нас есть что-то вроде g(n) = n² + 5n + 6, то О большое будет (n²). Если вы когда нибудь проводили некоторые исчисления, это очень похоже на сокращение пределов для дробных многочленов, когда вам важен только доминирующий оператор для числителей и знаменателей в конце.

Another way to look at Big O, Image from Stack Overflow
Но какая функция растет быстрее, чем другие? На самом деле существует довольно много правил.
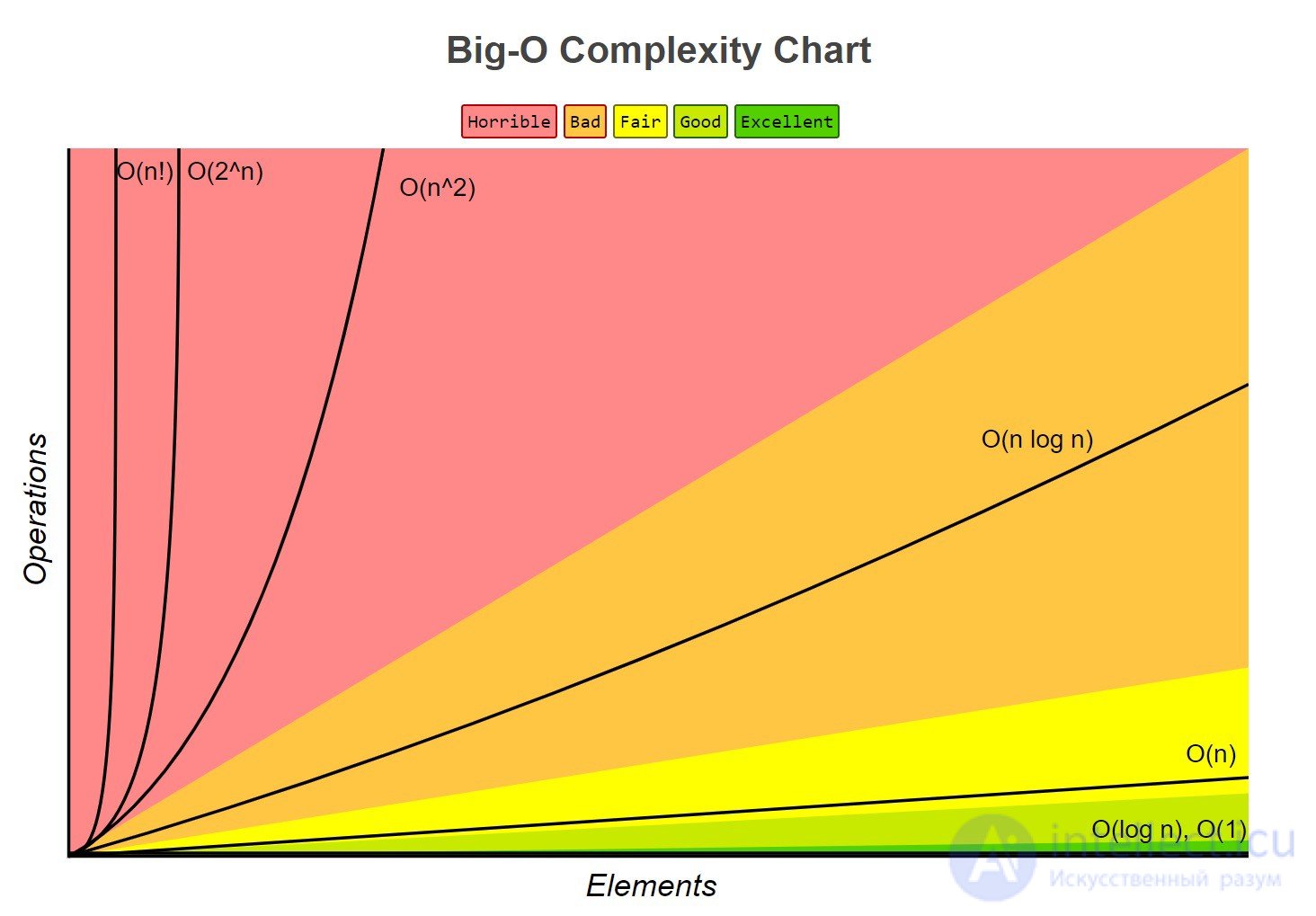
Complexity Growth Illustration from Big O Cheatsheet
Часто называемый «постоянный по времени», если вы можете создать алгоритм для решения проблемы с O(1), то это будет лучший выбор алгоритма. В некоторых сценариях сложность может выходить за пределы O(1), тогда мы можем проанализировать их, найдя ее аналог O(1/g(n)). Например, O(1/n) является более сложным, чем O(1/n²).
Поскольку сложность часто связана с алгоритмами «разделяй и властвуй», O (log(n)) — это, как правило, хорошая сложность, которую можно достичь для алгоритмов сортировки. O (log(n)) является менее сложным, чем O (√n), потому что функцию квадратного корня можно считать полиномом, где показатель степени равен 0,5.
Например, O (n⁵) является более сложным, чем O (n⁴).
O (2ⁿ) является более сложным, чем O (n⁹⁹), но O (2ⁿ) на самом деле является менее сложным, чем O(1). Обычно мы берем 2 в качестве основы для степеней и логарифмов, потому что в компьютерных науках все имеет тенденцию быть двоичным, но степень можно изменить, изменив коэффициенты. Если не указано иное, основание для логарифмов принимается равным 2.
Если вам интересны доказательства, посмотрите Гамма-функцию (Gamma function), это аналитическое продолжение факториала. Краткое доказательство состоит в том, что и факториалы, и степень имеют одинаковое количество умножений, но числа, которые умножаются, растут для факториалов, оставаясь неизменными для степени.
При умножении сложность будет больше, чем оригинал, но не больше, чем эквивалентность умножения чего-то более сложного. Например, O (n*log (n)) является более сложным, чем O (n), но менее сложным, чем O (n²), потому что O (n²) = O (n * n), а n более сложный, чем log (n). ).
Если хотите можете проверить свое понимание. Попробуйте ранжировать следующие функции от самых сложных до менее. Решения с подробными объяснениями можно будет найти в следующем разделе. Некоторые из них достаточно сложные и могут потребовать более глубокого понимания математики. Когда вы доберетесь до решения, вы узнаете об этом больше.
Вопрос: Расставьте следующие функции от самых сложных до менее.
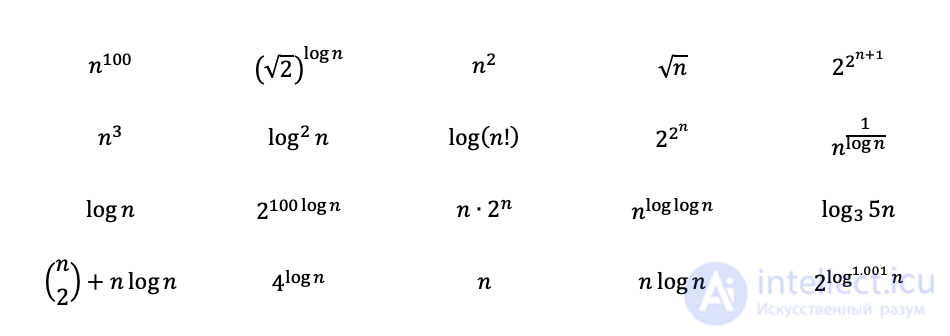
Examples taken from Textbook Problems
Решение для вопроса из Раздела 2:
На самом деле это был вопрос с подвохом, чтобы проверить ваше понимание. Возможно вы бы предположили что ответ равен O (n²), потому что есть вложенный цикл for. Но нужно понять, что входными данными является массив изображений, и каждый пиксель в алгоритме проходится только один раз, то ответ на самом деле будет O (n). В следующем разделе будут рассмотрены другие примеры, подобные этому.
До сих пор мы обсуждали только временную сложность алгоритмов. То есть мы заботимся только о том, сколько времени потребуется программе для выполнения задачи. Что также важно, так это место, занимаемое программой в памяти для выполнения задачи. Сложность пространства связана с тем, сколько памяти будет использовать программа, и, следовательно, также является важным фактором для анализа.
Пространственная сложность работает аналогично временной сложности. Например, сортировка выбором имеет пространственную сложность O(1), потому что она хранит только одно минимальное значение и свой индекс для сравнения, максимальное используемое пространство не увеличивается с размером ввода.
Некоторые алгоритмы, такие как блочная сортировка, имеют пространственную сложность O (n), но при этом в ней можно уменьшить временную сложность до O (1). Блочная сортировка это такая сортировка в котором сортируемые элементы распределяются между конечным числом отдельных блоков (карманов, корзин) так, чтобы все элементы в каждом следующем по порядку блоке были всегда больше (или меньше), чем в предыдущем. Каждый блок затем сортируется отдельно, либо рекурсивно тем же методом, либо другим. Затем элементы помещаются обратно в массив.
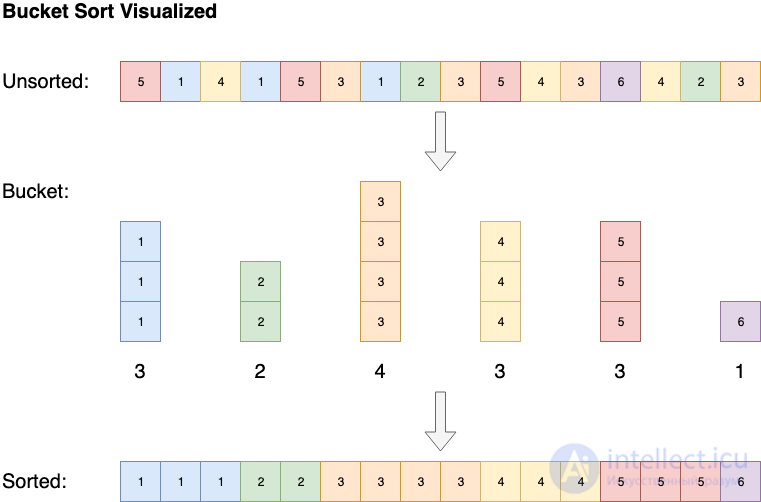
Bucket Sort Visualization
Сложность также может быть проанализирована как лучший случай, наихудший случай, средний случай и ожидаемый случай.
Для примера давайте рассмотрим сортировку вставками (insertion sort). Сортировка вставками выполняет итерацию по всем элементам в списке. Если элемент больше, чем его предыдущий элемент, он вставляет элемент назад, пока он не станет больше, чем предыдущий элемент.

Insertion Sort Illustrated, Image from Wikipedia
Если массив изначально отсортирован, обмен вообще не будет произведен. Алгоритм будет просто пройдет итерацию по массиву один раз, что приведет к временной сложности O (n). Следовательно, мы бы сказали, что наилучшая временная сложность сортировки вставками — O (n). Сложность O (n)
продолжение следует...
Часть 1 Анализ и оценка сложности алгоритмов, О большое, функции оценки сложности
Часть 2 Оптимальная сортировка - Анализ и оценка сложности алгоритмов, О большое,
Часть 3 Примеры - Анализ и оценка сложности алгоритмов, О большое, функции
Часть 4 Почему О большое может не имеет значения - Анализ и
А как ты думаешь, при улучшении сложность алгоритмов, будет лучше нам? Надеюсь, что теперь ты понял что такое сложность алгоритмов, оценка сложности алгоритмов, анализ сложности алгоритмов, большое o, доминирующий оператор, о большое, big o, рекурсивная сложность, логарифмическая сложность, сложность рекурсивных алгоритмов, функции оценки сложности, практическая оценка сложности алгоритмов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов