18.2. Энтропия как мера степени неопределенности состояния физической системы

Привет, Вы узнаете о том , что такое энтропия, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое энтропия , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

Любое сообщение, с которым мы имеем дело в теории информации, представляет собой совокупность сведений о некоторой физической системе. Например, на вход автоматизированной системы управления производственным цехом может быть передано сообщение о нормальном или повышенном проценте брака, о химическом составе сырья или температуре в печи. На вход системы управления средствами противовоздушной обороны может быть передано сообщение о том, что в воздухе находятся две цели, летящие на определенной высоте, с определенной скоростью. На тот же вход может быть передано сообщение о том, что на определенном аэродроме в данный момент находится такое-то количество истребителей в боевой готовности, или что аэродром выведен из строя огневым воздействием противника, или что первая цель сбита, а вторая продолжает полет с измененным курсом. Любое из этих сообщений описывает состояние какой-то физической системы.

 

Очевидно, если бы состояние физической системы было известно заранее, не было бы смысла передавать сообщение. Сообщение приобретает смысл только тогда, когда состояние системы заранее неизвестно, случайно.

Поэтому в качестве объекта, о котором передается информация, мы будем рассматривать некоторую физическую систему 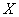, которая случайным образом может оказаться в том или ином состоянии, т. е. систему, которой заведомо присуща какая-то степень неопределенности. Очевидно, сведения, полученные о системе, будут, вообще говоря, тем ценнее и содержательнее, чем больше была неопределенность системы до получения этих сведений («априори»). Возникает естественный вопрос: что значит «большая» или «меньшая» степень неопределенности и чем можно ее измерить?

Чтобы ответить на этот вопрос, сравним между собой две системы, каждой из которых присуща некоторая неопределенность.

В качестве первой системы возьмем монету, которая в результате бросания может оказаться в одном из двух состояний: 1) выпал герб и 2) выпала цифра. В качестве второй - игральную кость, у которой шесть возможных состояний: 1, 2, 3, 4, 5 и 6. Спрашивается, неопределенность какой системы больше? Очевидно, второй, так как у нее больше возможных состояний, в каждом из которых она может оказаться с одинаковой вероятностью.

Может показаться, что степень неопределенности определяется числом возможных состояний системы. Однако в общем случае это не так. Рассмотрим, например, техническое устройство, которое может быть в двух состояниях: 1) исправно и 2) отказало. Предположим, что до получения сведений (априори) вероятность исправной работы устройства 0,99, а вероятность отказа 0,01. Такая система обладает только очень малой степенью неопределенности: почти наверное можно предугадать, что устройство будет работать исправно. При бросании монеты тоже имеется два возможных состояния, но степень неопределенности гораздо больше. Мы видим, что степень неопределенности физической системы определяется не только числом ее возможных состояний, но и вероятностями состояний.

Перейдем к общему случаю. Рассмотрим некоторую систему 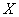, которая может принимать конечное множество состояний:  с вероятностями , где

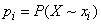                                  (18.2.1)

- вероятность того, что система 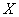 примет состояние  (символом  обозначается событие: система находится в состоянии ). Очевидно, .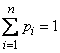

Запишем эти данные в виде таблицы, где в верхней строке перечислены возможные состояния системы, а в нижней - соответствующие вероятности:

Эта табличка по написанию сходна с рядом распределения прерывной случайной величины 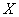 с возможными значениями , имеющими вероятности . И действительно, между физической системой 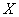 с конечным множеством состояний и прерывной случайной величиной много общего; для того чтобы свести первую ко второй, достаточно приписать каждому состоянию какое-то числовое значение (скажем, номер состояния). Подчеркнем, что для описания степени неопределенности системы совершенно неважно, какие именно значения  записаны в верхней строке таблицы; важны только количество этих значений и их вероятности.

В качестве меры априорной неопределенности системы (или прерывной случайной величины 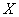) в теории информации применяется специальная характеристика, называемая энтропией. Понятие об энтропии является в теории информации основным.

Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком:

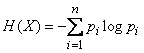.                      (18.2.2)

энтропия 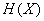 , как мы увидим в дальнейшем, обладает рядом свойств, оправдывающих ее выбор в качестве характеристики степени неопределенности. Об этом говорит сайт https://intellect.icu . Во-первых, она обращается в нуль, когда одно из состояний системы достоверно, а другие - невозможны. Во-вторых, при заданном числе состояний она обращается в максимум, когда эти состояния равновероятны, а при увеличении числа состояний - увеличивается. Наконец, и это самое главное, она обладает свойством аддитивности, т. е. когда несколько независимых систем объединяются в одну, их энтропии складываются.

Логарифм в формуле (18.2.2) может быть взят при любом основании 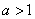. Перемена основания равносильна простому умножению энтропии на постоянное число, а выбор основания равносилен выбору определенной единицы измерения энтропии. Если за основание выбрано число 10, то говорят о «десятичных единицах» энтропии, если 2 - о «двоичных единицах». На практике удобнее всего пользоваться логарифмами при основании 2 и измерять энтропию в двоичных единицах; это хорошо согласуется с применяемой в электронных цифровых вычислительных машинах двоичной системой счисления.

В дальнейшем мы будем везде, если не оговорено противное, под символом  понимать двоичный логарифм.

В приложении (табл. 6) даны двоичные логарифмы целых чисел от 1 до 100.

Легко убедиться, что при выборе 2 в качестве основания логарифмов за единицу измерения энтропии принимается энтропия простейшей системы 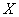, которая имеет два равновозможных состояния:

Действительно, по формуле (18.2.2) имеем:

.

Определенная таким образом единица энтропии называется «двоичной единицей» и иногда обозначается bit (от английского «binary digit» - двоичный знак). Это энтропия одного разряда двоичного числа, если он с одинаковой вероятностью может быть нулем или единицей.

Измерим в двоичных единицах энтропию системы 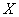, которая имеет  равновероятных состояний:

Имеем:

или

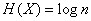,                       (18.2.3)

т. е. энтропия системы с равновозможными состояниями равна логарифму числа состояний.

Например, для системы с восемью состояниями .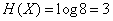

Докажем, что в случае, когда состояние системы в точности известно заранее, ее энтропия равна нулю. Действительно, в этом случае все вероятности  в формуле (18.2.2) обращаются в нуль, кроме одной - например , которая равна единице. Член 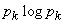 обращается в нуль, так как 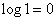. Остальные члены тоже обращаются в нуль, так как

.

Докажем, что энтропия системы с конечным множеством состояний достигает максимума, когда все состояния равновероятны. Для этого рассмотрим энтропию системы (18.2.2) как функцию вероятностей  и найдем условный экстремум этой функции при условии:

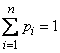.                   (18.2.4)

Пользуясь методом неопределенных множителей Лагранжа, будем искать экстремум функции:

.              (18.2.5)

Дифференцируя (18.2.5) по  и приравнивая производные нулю, получим систему уравнений:

  

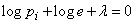
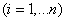
или

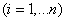     ,                  (18.2.6)

откуда видно, что экстремум (в данном случае максимум) достигается при равных между собой значениях 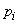. Из условия (18.2.4) видно, что при этом

,                                  (18.2.7)

а максимальная энтропия системы равна:

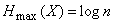,                              (18.2.8)

т. е. максимальное значение энтропии системы с конечным числом состояний равно логарифму числа состояний и достигается, когда все состояния равновероятны.

Вычисление энтропии по формуле (18.2.2) можно несколько упростить, если ввести в рассмотрение специальную функцию:

,                   (18.2.9)

где логарифм берется по основанию 2.

Формула (18.2.2) принимает вид:

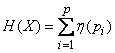.                 (18.2.10)

Функция 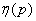 затабулирована; в приложении (табл. 7) приведены ее значения для  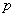от 0 до 1 через 0,01.

Пример 1. Определить энтропию физической системы, состоящей из двух самолетов (истребителя и бомбардировщика), участвующих в воздушном бою. В результате боя система может оказаться в одном из четырех возможных состояний:

1) оба самолета не сбиты;

2) истребитель сбит, бомбардировщик не сбит;

3) истребитель не сбит, бомбардировщик сбит;

4) оба самолета сбиты.

Вероятности этих состояний равны соответственно 0,2; 0,3; 0,4 и 0,1.

Решение. Записываем условия в виде таблицы:

	0,2	0,3	0,4	0,1

По формуле (18.2.10) имеем:

.

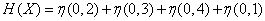Пользуясь таблицей 7 приложения, находим

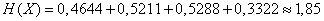(дв. ед.).

Пример 2. Определить энтропию системы, состояние которой описывается прерывной случайной величиной 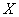 с рядом распределения

	0,01	0,01	0,01	0,01	0,96

Решение.

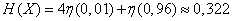 (дв. ед.).

Пример 3. Определить максимально возможную энтропию системы, состоящей из трех элементов, каждый из которых может быть в четырех возможных состояниях.

Решение. Общее число возможных состояний системы равно 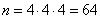. Максимально возможная энтропия системы равна  (дв. ед.).

Пример 4. Определить максимально возможную энтропию сообщения, состоящего из пяти букв, причем общее число букв в алфавите равно 32.

Решение. Число возможных состояний системы 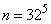. Максимально возможная энтропия равна  (дв. ед).

Формула (18.2.2) (или равносильная ей (18.2.10)) служит для непосредственного вычисления энтропии. Однако при выполнении преобразований часто более удобной оказывается другая форма записи энтропии, а именно, представление ее в виде математического ожидания:

,                   (18.2.11)

где 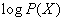 - логарифм вероятности любого (случайного) состояния системы, рассматриваемый как случайная величина.

Когда система 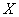 принимает состояния , случайная величина 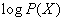 принимает значения:

.                                (18.2.12)

Среднее значение (математическое ожидание) случайной величины - 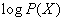 и есть, как нетрудно убедиться, энтропия системы 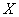. Для ее получения значения (18.2.12) осредняются с «весами», равными соответствующим вероятностям .

Формулы, подобные (18.2.11), где энтропия представляется в виде математического ожидания, позволяют упрощать преобразования, связанные с энтропией, сводя их к применению известных теорем о математических ожиданиях.

 

Информация, изложенная в данной статье про энтропия , подчеркивают роль современных технологий в обеспечении масштабируемости и доступности. Надеюсь, что теперь ты понял что такое энтропия и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов