Лекция
Сразу хочу сказать, что здесь никакой воды про числовые алгоритмы, и только нужная информация. Для того чтобы лучше понимать что такое числовые алгоритмы , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
Классификация чисовых Алгоритмов
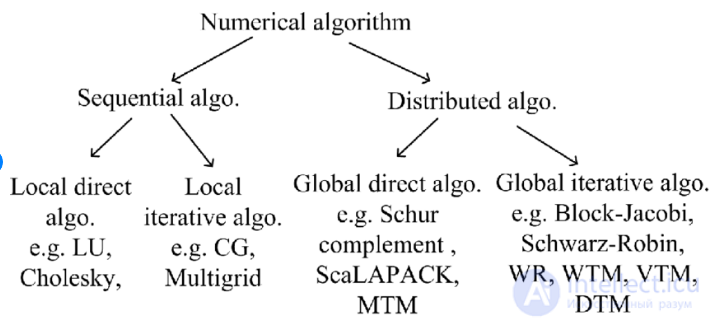
Прежде чем начинать изложение, нам необходимо формализовать понятие сложности алгоритма – некоторой счетной последовательности
действий. Мы будем измерять сложность алгоритма некоторой величиной, позволяющей охарактеризовать алгоритм с точки зрения его практической применимости. Чем меньше данная величина, тем больше целесообразность применения данного алгоритма.

Определение 1. Под сложностью алгоритма мы будем подразумевать количество выполняемых в ходе алгоритма операций над элементами некоторого конечного множества. Для сложности алгоритма мы также будем использовать синоним — трудоемкость алгоритма.
Из нашего определения сразу следует, что понятие сложности не однозначно и зависит от выбора конечного множества, над которым производятся вычисления. Существует два подхода при выборе множества операндов — первый основывается на фиксации некоторого математического объекта, например, группы или кольца. Второй подход основывается на фиксации длины регистров вычислительного средства, которое будет реализовывать данный алгоритм. Первый подход более прост, универсален и принят в математических исследованиях, второй подход привязан к вычислительному средству, более точен и позволяет оценить
сложность алгоритма в тактах работы вычислительного средства. Мы будем использовать первый подход, оставляя детальный анализ разработчикам программного обеспечения.
В обоих случаях рассматривается некоторый параметр n, характеризующий множество, элементами которого оперирует алгоритм. Сложность алгоритма представляется в виде функции от n.
Пусть n > 0 — произвольная целая или действительная переменная.
Напомним, что символом O (f(n)) обозначается функция такая, что

где c > 0 некоторая константа. Рассмотрим функцию
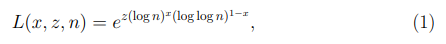
действительных переменных  целая или действительная переменная.
целая или действительная переменная.
Определение 2. Пусть f(n) — функция, задающая сложность алгоритма, функция L(x, z, n) определена равенством (1), значения x, z
фиксированы и  . Мы будем использовать следующую терминологию.
. Мы будем использовать следующую терминологию.
1. Функция f(n) называется полиномиальной, если
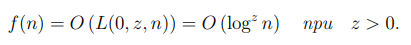
2. Функция f(n) называется экспоненциальной, если
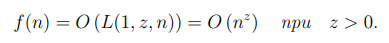
3. Функция f(n) называется субэкспоненциальной, если
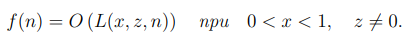
Рассмотрим также частные случаи.
4. Если f(n) = O (1) или, что равносильно, z = 0 при любом значении x, то f(n) называется константой.
5. Если f(n) = O (n) экспоненциальна при z = 1, то f(n) называется сложностью тотального перебора.
Как видно из данного определения, субэкспоненциальная функция занимает промежуточное положение между полиномиальной и эспоненциальной функциями. Действительно при фиксированных значениях z и n > 1 получаем
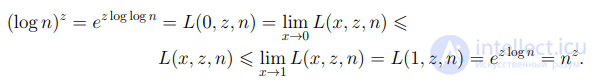
.
Здесь мы неявно используем тот факт, что при фиксированных значениях z, n функция L(x, z, n) является монотонно неубывающей функцией.
Отметим одну особенность, возникающую при решении криптографических задач. Все рассматриваемые нами задачи обязательно имеют
решение, поиск которого может быть сведен к перебору всех элементов некоторого конечного множества, характеризуемого целочисленным параметром n. Следовательно, максимальная сложность решения подобной задачи определяется сложностью тотального перебора, то есть O (n).
Однако в используемых на практике приложениях значение параметра n настолько велико, что применение тотального перебора не позволяет
найти решение за приемлемое время, даже с использованием максимально производительных вычислительных средств. В связи с этим, наша
задача сводится к поиску алгоритмов, имеющих сложность, меньшую сложности тотального перебора.
Отметим, что существование полиномиального, то есть быстрого алгоритма решения рассматриваемых нами задач является, скорее, приятным исключением, чем правилом. Задач, имеющих полиномиальные алгоритмы решения, крайне не много, большинство из них мы перечисляем ниже:
Для остальных задач, рассматриваемых нами, достижимый минимум сложности – существование субэкспоненциального алгоритма.
Теперь рассмотрим еще один способ классификации алгоритмов. Традиционно принято подразделять все алгоритмы на детерминированные
и вероятностные. Для детерминированного алгоритма оценка сложности вычисляется однозначно, в то время как для вероятностного алгоритма оценка сложности вычисляется при некоторых предположениях, которые могут существенно влиять на получаемые результаты. Приведем некоторые примеры и поясним вышесказанное.
Определение 3. Алгоритм называется детерминированным, если после фиксированного числа шагов (операций над элементами конечного множества) результат работы данного алгоритма всегда является решением поставленной задачи. Отметим, что слово «всегда» в приведенном определении является
существенно важным.
Определение 4. Мы будем называть алгоритм вероятностным, если выполнено одно из следующих утверждений
Собственно один и тот же алгоритм может рассматриваться и как детерминированный, и как вероятностный, в зависимости от нашего толкования этого термина, либо от попытки минимизировать его сложность.
Рассмотрим следующий пример. Пусть у нас имеется урна, в которой находится n шаров – один красный и n − 1 черных шаров. Мы можем
вытаскивать из урны шары, не возвращая их на место. Наша задача вытащить красный шар.
Если мы подряд вытащим из урны все n шаров, то среди них обязательно окажется красный шар, следовательно, мы получаем детерминированный алгоритм. Сложность этого алгоритма равна n выниманий шара из урны.
Теперь опишем вариант решения той же задачи с помощью вероятностного алгоритма, удовлетворяющего первому утверждению нашего
определения.
Зафиксируем число попыток вытащить шар из урны и обозначим его символом k. В этом случае вероятность успешного завершения алгоритма, или другими словами, вероятность того, что мы не вытащим k черных шаров подряд, будет равна 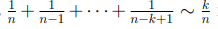 при небольших значениях k.
при небольших значениях k.
Таким образом, если мы хотим иметь полиномиальный алгоритм, то выберем  , при этом вероятность его успешного завершения мала и равна
, при этом вероятность его успешного завершения мала и равна
l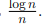 . Очевидно, что при k = n мы получим описанные ранее детерминированный алгоритм, поскольку вероятность его успешного завершения равна единице.
. Очевидно, что при k = n мы получим описанные ранее детерминированный алгоритм, поскольку вероятность его успешного завершения равна единице.
Зафиксируем вероятность успешного завершения алгоритма и обозначим ее символом p, 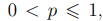 , тогда среднее число шагов, необходимых для успешного завершения алгоритма, равно pn. Таким образом, фиксация вероятности успеха приводит к определению трудоемкости алгоритма. Если мы положим вероятность равной единице, то мы, очевидно, получим, что среднее число шагов алгоритма (вытаскиваний шара из урны) равно n. Это второй вариант вероятностного алгоритма в нашем определении.
, тогда среднее число шагов, необходимых для успешного завершения алгоритма, равно pn. Таким образом, фиксация вероятности успеха приводит к определению трудоемкости алгоритма. Если мы положим вероятность равной единице, то мы, очевидно, получим, что среднее число шагов алгоритма (вытаскиваний шара из урны) равно n. Это второй вариант вероятностного алгоритма в нашем определении.
Третий вариант алгоритма в нашем определении может быть получен, если мы будем возвращать вынутые черные шары обратно в урну. В этом случае существует вероятность, что мы так и не вытащим красный шар, то есть не завершим выполнение алгоритма.
Суммируя изложенное, заметим, что мы могли бы изначально определить понятие сложности алгоритма, как функцию двух аргументов —
количества выполненных им шагов и вероятности успешного завершения алгоритма. Однако такой подход к исследованию трудоемкости не
является общепринятым. В дальнейшем, если это не оговорено особо,
мы будем оценивать сложность вероятностных алгоритмов в предположении, что вероятность их успешного завершения не менее 1/2
Мы начнем изложение с простейших вопросов и рассмотрим множество целых чисел .
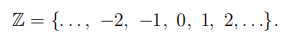
Множество целых чисел образует кольцо относительно операций сложения и умножения. Введем на этом множестве операцию деления.
Определение 1.1. Пусть a, b целые числа. Мы будем говорить, что a делит b и использовать запись a|b, если найдется такое целое число d, что ad = b.
Хорошо известно, что операция деления не может быть определена для двух произвольных целых чисел a, b. Легко привести пример, например, число 3 не делит число 7, ибо нельзя найти целое число d такое, что 3d = 7.
С другой стороны, мы можем ввести другую операцию — операцию деления с остатком, которая определена для любой пары целых чисел
a, b. Нам потребуется следующая лемма.
Лемма 1.1. Пусть a, b целые числа, тогда существуют единственные целые числа q, r такие, что

Доказательство. Без ограничения общности будем считать, что a > 0. Тогда найдется наибольшее целое число q такое, что aq 6 b и b < a(q+1).
Обозначая r = b − aq, получим неравенство 0 6 r < a и представление (1.1). Допустим, что представление (1.1) не единственно. Тогда найдутся такие целые числа q1, r1, что выполнены равенства b = aq1 + r1 и aq + r = aq1 + r1.
Из последнего равенства следует, что a|(r1 − r). Из определения чисел r, r1 сдедует, что |r1 − r| < a. Таким образом, r1 − r = 0 и r1 = r, q1 = q.Лемма доказана.
Определение 1.2. Пусть a, b целые числа. Мы будем называть целое число r 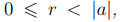 , остатком от деления b на a, если выполнено
, остатком от деления b на a, если выполнено
представление (1.1) или, что аналогично, a|(b − r).
Алгоритмы:
Введем одно из фундаментальных понятий в алгебре и теории чисел,
а именно, понятие вычета по модулю целого числа.
Определение 2.1. Пусть a, b целые числа, и m > 0 натуральное число. Мы будем говорить, что числа a и b сравнимы по модулю m и записывать 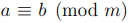 , если m|(a − b) или, что аналогично, a = b + km для некоторого целого значения k.
, если m|(a − b) или, что аналогично, a = b + km для некоторого целого значения k.
Из определения 2.1 следует, что решениями сравнения 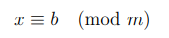 являются все целые числа вида b + km, где k некоторое целое число.
являются все целые числа вида b + km, где k некоторое целое число.
Данные числа образуют класс чисел по модулю m.
Определение 2.2. Об этом говорит сайт https://intellect.icu . Любое число из класса 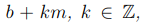 , мы будем называть вычетом по модулю числа m. Вычет x, удовлетворяющий
, мы будем называть вычетом по модулю числа m. Вычет x, удовлетворяющий
неравенству 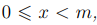 , будем называть наименьшим неотрицательным вычетом. Возьмем из каждого класса по модулю m по одному представителю – наименьшему неотрицательному вычету. Легко видеть, что таких вычетов всего m штук и все они различны.
, будем называть наименьшим неотрицательным вычетом. Возьмем из каждого класса по модулю m по одному представителю – наименьшему неотрицательному вычету. Легко видеть, что таких вычетов всего m штук и все они различны.
Определение 2.3. Мы будем называть полной системой вычетов множество всех наименьших неотрицательных вычетов по модулю m.
В дальнейшем нам потребуется и другой способ определения представителей классов вычетов, основанный на величине абсолютного значения
представителя.
Определение 2.4. Мы будем называть абсолютно-наименьшим вычетом по модулю числа m вычет x, если он удовлетворяет неравенству
1.  при четном m;
при четном m;
2. 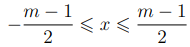 при нечетном m.
при нечетном m.
Определение 2.5. Аналогично определению 2.3, мы будем называть полной системой абсолютно-наименьших вычетов – множество всех абсолютно-наименьших вычетов по модулю m.
Алгоритмы:
Формализуем наши знания о многочленах: введем формальное понятие многочлена от одной переменной, определим для многочленов операции сложения, умножения и деления с остатком, покажем, что для многочленов также можно доказать теорему об однозначном разложении на множители.
Мы будем обозначать символом  произвольное коммутативное кольцо с единицей. В качестве примеров таких колец можно рассмотреть кольцо целых чисел
произвольное коммутативное кольцо с единицей. В качестве примеров таких колец можно рассмотреть кольцо целых чисел 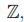 , кольцо
, кольцо 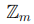 вычетов по модулю целого числа m. Поскольку поля также являются и кольцами, то в качестве кольца
вычетов по модулю целого числа m. Поскольку поля также являются и кольцами, то в качестве кольца 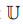 мы будем рассматривать поля рациональных чисел
мы будем рассматривать поля рациональных чисел  действительных чисел
действительных чисел 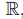 а также конечное поле
а также конечное поле 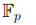
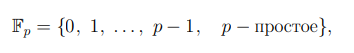 которое образует полная система вычетов по модулю простого числа p.
которое образует полная система вычетов по модулю простого числа p.
Доказательство того факта, что множество 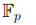 действительно образует поле, заключается в проверке всех аксиом и вытекает из результатов
действительно образует поле, заключается в проверке всех аксиом и вытекает из результатов
предыдущей главы.
Определение 3.1. Пусть U произвольное коммутативное кольцо с единицей, a, b – ненулевые элементы кольца U. Мы будем говорить, что a делит b и использовать обозначение a|b или b ≡ 0 (mod a), если в кольце U найдется такой элемент d, что ad = b. Элемент a мы будем называть делителем числа b.
Очевидно, что для кольца целых чисел Z это определение совпадает с введенным ранее определением 1.1.
Определение 3.2. Мы будем называть элемент ε кольца U обратимым, если он является делителем единицы, то есть для него найдется некоторый элемент ε
−1 того же кольца такой, что 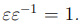 . Для обозначения обратного элемента мы также будем использовать обозначение 1 /ε.
. Для обозначения обратного элемента мы также будем использовать обозначение 1 /ε.
Относительно операции умножения обратимые элементы образуют группу. Действительно, если a, b два обратимых элемента кольца U, то
существуют элементы  такие, что
такие, что 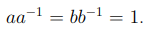 . Тогда, в силу коммутативности кольца U, получаем равенство
. Тогда, в силу коммутативности кольца U, получаем равенство
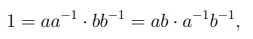
из которого следует, что элемент ab также является обратимым. В кольце целых чисел Z существует всего два обратимых элемента 1 и −1, которые также содержатся и в любом другом кольце. Произвольные кольца могут содержать более двух обратимых элементов, например, в поле все отличные от нуля элементы обратимы. Обратимый элемент ε делит любой элемент кольца U. Действительно, для любого элемента a выполнено равенство 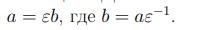
.
Пример 3.1. Рассмотрим кольцо вычетов 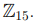 . Тогда группа его обратимых элементов состоит из следующих вычетов Z
. Тогда группа его обратимых элементов состоит из следующих вычетов Z
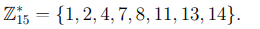
Из леммы Безу, см. лемму 2.2, следует, что обратимыми элементами являются только вычеты, взаимно простые с модулем. Количество
таких чисел определяется значением функции Эйлера  и, согласно теореме 2.5, равно 8.
и, согласно теореме 2.5, равно 8.
Дадим несколько важных определений и введем понятие кольца многочленов от одной переменной U[x], которое будет многократно использовано нами в дальнейшем.
Определение 3.3. Пусть U произвольное коммутативное кольцо с единицей и 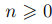 целое число. Многочленом a(x) от одной переменной x мы будем называть сумму
целое число. Многочленом a(x) от одной переменной x мы будем называть сумму 
Величины 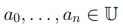 мы будем называть коэффициентами многочлена, коэффициент an – старшим коэффициентом.
мы будем называть коэффициентами многочлена, коэффициент an – старшим коэффициентом.
При некотором фиксированном значении x ∈ U значением многочлена a(x) мы будем называть значение выражения (3.1), принадлежащее кольцу U.
Целое число n мы будем называть степенью многочлена и обозначать символом deg a(x) = n. Многочлены степени один мы будем называть линейными.
Как следует из данного нами определения, все элементы кольца U могут рассматриваться как многочлены нулевой степени. Это утверждение неверно лишь для нуля, ибо у него всегда выполнено an = 0. Поэтому
мы будем дополнительно считать, что deg 0 = −1.
Определение 3.4. Многочлен 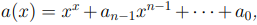 , старший коэффициент которого равен единице, называется унитарным1
, старший коэффициент которого равен единице, называется унитарным1
.
Далее мы будем обозначать символом U[x] множество многочленов от одной переменной x с коэффициентами из кольца U. Пусть
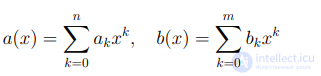
два произвольных многочлена. Без ограничения общности будем считать, что 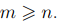 . Определим их сумму равенством
. Определим их сумму равенством
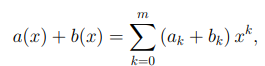
где коэффициенты an+1, . . . , am полагаются равными нулю. Легко видеть, что 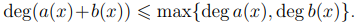 Знак «меньше» возникает в том случае, когда сумма старших коэффициентов равна нулю.
Знак «меньше» возникает в том случае, когда сумма старших коэффициентов равна нулю.
Определим произведение многочленов равенством
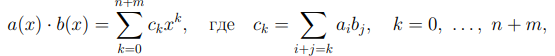
также выполнено равенство 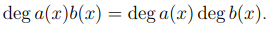
В русскоязычных изданиях нет устоявшегося названия для данного многочлена. В литературе по теории чисел традиционно используется понятие примитивного многочлена, в пособиях по алгебре – понятия унитарного, нормированного или приведенного многочлена.
Введенные нами операции позволяют определить на множестве U[x] структуру коммутативного кольца, единица и ноль которого совпадают
с единицей и нулем кольца U. Доказательство этого утверждения проводится проверкой всех свойств, которым должно удовлетворять кольцо.
Мы будем говорить, что многочлен
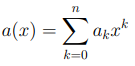
делит многочлен b(x), если для некоторого многочлена u(x) ∈ U[x] выполнено равенство a(x)u(x) = b(x). Исходя из определения операции
умножения многочленов, мы сразу заключаем, что deg a(x) 6 deg b(x).
Заметим, что если старший коэффициент an многочлена a(x) является обратимым, то мы можем записать многочлен a(x) в виде
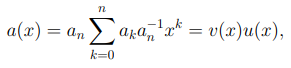
где 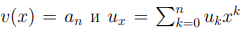 унитарный многочлен, коэффициенты которого определены равенствами
унитарный многочлен, коэффициенты которого определены равенствами 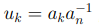 для k = 0, . . . , n.
для k = 0, . . . , n.
Таким образом, многочлен a(x) ∈ U[x] с обратимым старшим коэффициентом может быть представлен в виде произведения многочлена нулевой степени на унитарный многочлен степени, равной степени многочлена a(x). Очевидно, что если кольцо U является полем, то это верно
для любого многочлена положительной степени.
Определение 3.5. Если многочлен a(x) ∈ U[x] называется неприводимым, если равенство a(x) = u(x)v(x), где u(x), v(x) ∈ U[x] возможно только в том случае, когда один из многочленов u(x), v(x) имеет нулевую степень и, таким образом, является элементом кольца U. Решение задачи о проверке, является ли заданный многочлен неприводимым, существенно зависит от кольца, над которым рассматривается многочлен. Как хорошо известно из курса алгебры, любой многочлен
с коэффициентами из поля комплексных чисел является приводимым, поскольку раскладывается на линейные множители, см. [5, гл.6, § 3]. Для произвольного кольца это, конечно, неверно. Однако мы можем доказать теорему о разложении многочленов на множители, аналогичную основной теореме арифметики для целых чисел.
Пусть a(x) и b(x) два многочлена из кольца U[x], при этом старший коэффициент многочлена a(x) является обратимым, в частности, a(x)
может быть унитарным многочленом. Аналогично кольцу целых чисел Z, введем операцию деления многочленов с остатком и определим два многочлена q(x), r(x) кольца U[x], удовлетворяющих равенству b(x) = a(x)q(x) + r(x), deg r(x) < deg a(x). (3.2)
Многочлен q(x) мы будем называть частным от деления, а многочлен r(x) – остатком от деления многочленов. Мы дадим определение операции деления с остатком при помощи следующего алгоритма, который часто называют «школьным алгоритмом деления многочленов».
Алгоритмы:
Рассмотрим непрерывные дроби действительных чисел.
Определение 5.1. Пусть α действительное число. Мы будем называть целой частью α, которую мы обозначаем символом  , наибольшее целое число, меньшее, либо равное α. В частном случае: целая часть целого числа совпадает с ним.
, наибольшее целое число, меньшее, либо равное α. В частном случае: целая часть целого числа совпадает с ним.
Отметим, что α может быть как отрицательным, так и положительным числом.
Например  , в то время как
, в то время как 

В любом случае выполнено неравенство 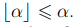
Пусть α0 действительное число и 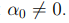 . Определим последовательность действительных чисел α1, α2, . . . следующим реккурентным соотношением
. Определим последовательность действительных чисел α1, α2, . . . следующим реккурентным соотношением
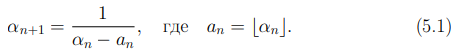
В случае, если αn является целым числом, то есть выполнено равенство an = αn, мы будем считать, что последовательность (5.1) обрывается.
Записав равенство (5.1) в виде  , мы можем выразить число α0 в виде
, мы можем выразить число α0 в виде

или, в общем виде,
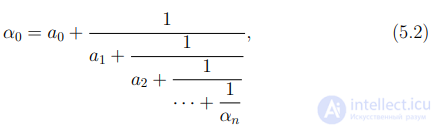
для произвольного индекса n.
Для упрощенной записи равенства (5.2) мы будем использовать обозначение 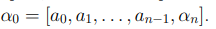
Определение 5.2. Пусть 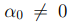 действительное число. Мы будем называть представление (5.2)
действительное число. Мы будем называть представление (5.2)

n = 1, 2, . . . непрерывной или цепной дробью числа α0. Элементы последовательности a0, a1, . . . мы будем называть неполными частными,
а элементы последовательности α1, α2, . . . полными частными.
Заметим, что из соотношения (5.1) и неравенства 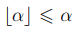 вытекает выполнимость следующих неравенств
вытекает выполнимость следующих неравенств
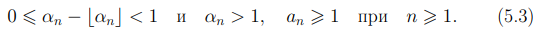
Алгоритмы:
В криптографических приложениях простые числа играют важную
роль, являясь долговременными параметрами криптографических схем
и подвергаясь атакам нарушителей в первую очередь. Время действия
открытых параметров ограничено, что вынуждает разработчиков криптографических схем достаточно часто вырабатывать новые, не использовавшиеся ранее простые числа.
При выработке простых чисел, на них, как правило, накладываются дополнительные условия. Приведем пример: согласно первой редакции стандарта Российской Федерации на электронную цифровую подпись ГОСТ Р 34.10-94, необходимо построить два простых числа p, q,
удовлетворяющих условиям
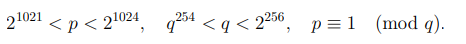
Следующая редакция стандарта накладывает несколько другие условия на простые числа p, q:
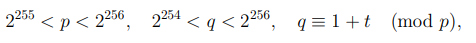
для некоторого целого t, удовлетворяющего неравенству 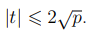 . При генерации простых чисел, как правило, возникает два вопроса.
. При генерации простых чисел, как правило, возникает два вопроса.
1. Как построить простое число с заданными ограничениями на размер числа?
2. Как определить, является ли заданное целое число m простым или составным?
Данные вопросы тесно связаны между собой: как только у нас появляется критерий проверки простоты, мы сразу можем предложить алгоритм построения простого числа, основанный на данном критерии.
Кроме того, задача проверки простоты числа связана с задачей разложения на множители. Наиболее простой способ проверить, является ли число m составным или нет, это проверить утверждение леммы 1.6, то есть выяснить, существует ли у числа m простой делитель, не превосходящий величины  . Если такого делителя нет, то число m является простым. Для перебора всех возможных делителей нам потребуется сделать около
. Если такого делителя нет, то число m является простым. Для перебора всех возможных делителей нам потребуется сделать около  операций пробного деления числа m. При больших значениях числа m эта процедура становится не реализуемой на практике.
операций пробного деления числа m. При больших значениях числа m эта процедура становится не реализуемой на практике.
Вместе с тем, пробное деление часто используется для проверки: есть ли у числа маленькие делители.
Приведем алгоритм построения таблицы всех простых чисел, ограниченных сверху некоторой величиной b. Подобные таблицы будут нами использованы как для реализации метода пробного деления, так и в некоторых алгоритмах разложения целых чисел на множители.
Алгоритмы:
Рассмотрим элементарные методы разложения составного числа m на множители. Эти методы достаточно просты для изложения, но имеют высокую трудоемкость, что не позволяет их использовать для разложения чисел, используемых на практике. Тем не менее, излагаемые алгоритмы могут быть использованы в качестве составных частей в более сложных алгоритмах.
На протяжении всей главы мы будем считать, что m > 0 нечетное, составное число. Вопрос о том, как определить: является ли число m
составным или простым, мы рассматривали в предыдущей главе.
Напомним, что под задачей факторизации мы подразумеваем нахождение таких простых чисел 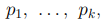 , что число m может быть единственным образом представлено в виде произведения
, что число m может быть единственным образом представлено в виде произведения

где αi натуральные числа. Такое представление, в силу основной теоремы арифметики, см. теорему 1.4, существует и единственно.
Для поиска всех простых делителей числа m нам необходимо найти два делителя числа m, быть может, и не простых, а потом применить
процедуру поиска делителей к каждому из найденных делителей. Далее мы будем описывать алгоритмы предполагая, что нам достаточно найти
два произвольных делителя числа m.
Алгоритмы:
Рассмотрим методы решения задачи дискретного логарифмирования
в мультипликативной группе конечного поля Fp.
Определение 9.1. Пусть заданы простое число p и вычет a, показатель которого по модулю p равен m, то есть 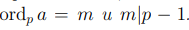
Пусть задан вычет b, удовлетворяющий сравнению

Задача определения вычета x (mod m) называется задачей вычисления индекса элемента b по основанию a. В криптографической литературе
задача вычисления индекса получила синонимичное название: «задача дискретного логарифмирования».
Для вычета x, удовлетворяющего сравнению (9.1), принято использовать обозначение
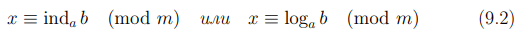
и называть его индекс или дискретный логарифм b по основанию a.
Из данного выше определения и утверждения леммы 2.3 вытекает, что сравнение (9.1) разрешимо только в том случае, когда вычет b принадлежит множеству

то есть является элементом циклической группы, порожденной элементом a. Мы будем также говорить, что в этом случае вычет b принадлежит
множеству возможных степеней вычета a по модулю p.
Прежде чем описывать методы решения задачи дискретного логарифмирования, мы опишем основные свойства индексов.
Лемма 9.1. Пусть задано простое число p и вычет a, показатель которого по модулю p равен m, то есть 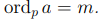 . Пусть задан вычет
. Пусть задан вычет
b, принадлежащий множеству возможных степеней вычета a по модулю p. Тогда выполнены следующие утверждения.
1. Выполнено сравнение loga a ≡ 1 (mod m).
2. Пусть для вычета b выполнено равенство

где α1, . . . , αn произвольные натуральные числа, а вычеты b1, . . .,
bn принадлежат множеству A возможных степеней вычета a.
Тогда

3. Выполнено сравнение 
4. Пусть для вычетов  тогда выполнено
тогда выполнено 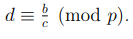
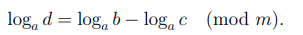
Доказательство. Первое утверждение леммы выполнено по определению. Для доказательства второго утверждения рассмотрим случай, когда 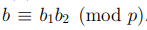 Поскольку вычеты b1 и b2 принадлеждат множеству возможных степеней вычета a, то найдутся такие вычеты x, y, что
Поскольку вычеты b1 и b2 принадлеждат множеству возможных степеней вычета a, то найдутся такие вычеты x, y, что
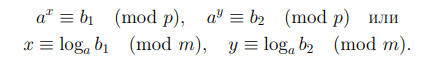
Перемножая вычеты b1 и b2, мы получим 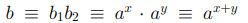 (mod p).
(mod p).
Следовательно, выполнено сравнение
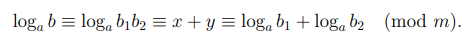
Обобщая это сравнение на случай 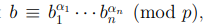 , мы получим
, мы получим
второе утверждение леммы. Легко видеть, что третье и четвертое утверждения леммы являются следствиями из второго утверждения.
Пример 9.1. Особо стоит обратить внимание на тот факт, что в условии
леммы 9.1 требуется принадлежность вычетов b1, . . . , bn циклической
подгруппе, порожденной вычетом a. Приведем пример, в котором нарушение этого условия приводит к опровержению утверждения леммы.
Рассмотрим уравнение
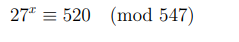
и заметим, что 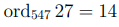 , то есть, вычет 27 не является первообразным корнем и порождает мультипликативную группу
, то есть, вычет 27 не является первообразным корнем и порождает мультипликативную группу
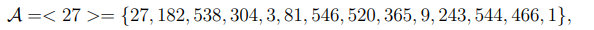
состоящую из 14 элементов. Легко видеть, что решение нашего уравнения существует и x = 8.
С другой стороны, выполнено равенство 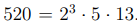 Применяя
Применяя
для нахождения неизвестного x утверждение леммы 9.1, мы должны записать сравнение
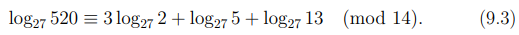
Поскольку вычеты 2, 5 и 13 не принадлежат группе A, то индексы 
 и
и 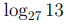 не существуют, следовательно, правая часть сравнения
не существуют, следовательно, правая часть сравнения
(9.3) не существует. Таким образом, получено противоречие со вторым утверждением леммы 9.1
Алгоритмы:
А как ты думаешь, при улучшении числовые алгоритмы, будет лучше нам? Надеюсь, что теперь ты понял что такое числовые алгоритмы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов