Поиск максимального паросочетания

Привет, сегодня поговорим про поиск максимального паросочетания, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое поиск максимального паросочетания , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

Пусть дан неориентированный граф G = (V, Е). Паросочетанием (matching) называется подмножество ребер М є Е, такое что для всех вершин v е V в М содержится не более одного ребра, инцидентного v.

Максимальным паросочетанием называется паросочетание максимальной мощности, т.е. такое паросочетание М, что для любого паросочетания М': |М| >= |М'|.

Ограничимся рассмотрением задачи поиска максимальных паросочетаний в двудольных графах. Мы предполагаем, что множество вершин можно разбить на два подмножества V = L U R, где L и R не пересекаются, и все ребра из Е проходят между L и R. Далее мы предполагаем, что каждая вершина из V имеет по крайней мере одно инцидентное ребро.

С помощью метода Форда-Фалкерсона можно найти максимальное паросочетание в неориентированном двудольном графе G = (V,E) за время, полиномиально зависящее от |V| и |Е|. Определим для заданного двудольного графа G соответствующую транспортную сеть G' = (V', Е') следующим образом. Возьмем в качестве источника s и стока t новые вершины, не входящие в V, и пусть V' = V U {s, t}. Если разбиение вершин в графе G задано как V = L U R, ориентированными ребрами G будут ребра Е, направленные из L в R, а также |V| новых ребер. Чтобы завершить построение, присвоим каждому ребру Е' единичную пропускную способность.

Ниже показан двудольный граф и соответствующая ему транспортная сеть. Выделенные ребра обеспечивают максимальный поток и определяют максимальное паросочетание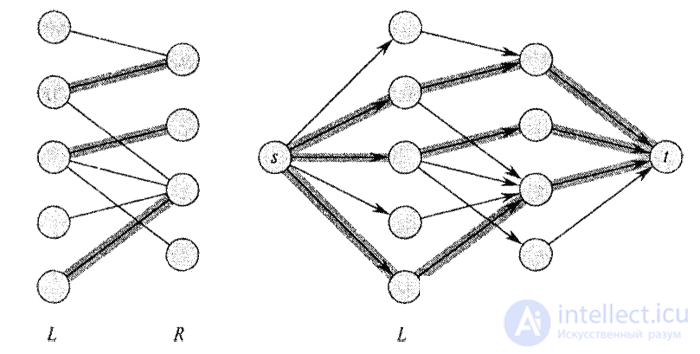

Формальное описание     [вверх]

Matching(G)
1. Об этом говорит сайт https://intellect.icu  . Проверить, является ли граф двудольным.
2. Если граф двудольный, то перейти к пункт 2.1., иначе 
   вывести сообщение о том, что граф недвудольный и завершить работу.
   2.1. Разбить граф на 2 части.
   2.2. Создать 2 вершини, связать стартовую со своеми вершинами 
        из первой части графа, конечную - со всеми вершинами 
        из второй части графа.
   2.3. Модернизировать полученную сеть, изменяя пропускную способность 
        в обратну сторону графа на отрицательные значения.
   2.4. Найти максимальный поток с помощью алгоритма Форда-Фалкерсона.
   2.5. Считать ребра между двумя частями графа 
        с потоком равным 1 ребрами паросочитаний.
   2.6. Подсчитать количество ребер в паросочитании.

Оценка сложности     [вверх]

Поскольку любое паросочетание в двудольном графе имеет мощность не более min(L, R) = О (V), величина максимального потока в G составляет О (V). Поэтому максимальное паросочетание в двудольном графе можно найти за время O(V*E') = O(V*E), поскольку |Е'| = o(Е).

Пример     [вверх]

Рассмотрим схему сведения двудольного графа к некоторой сети. На рисунке показан исходный двудольный граф G.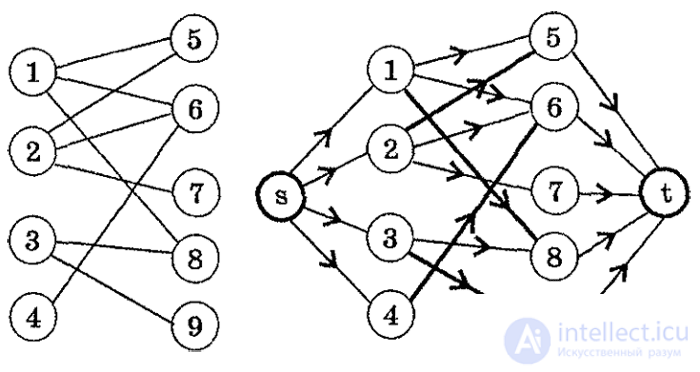 

Построим сеть S(G) с источником s и стоком t следующим образом:
* источник s соединим дугами с вершинами из множества X;
* вершины из множества Y соединим дугами со стоком t;
* направление на ребрах исходного графа будет от вершин из X к вершинам из Y;
* пропускная способность всех дуг C[i,j] = 1.
Найдем максимальный поток из s в t для построенной сети. Он существует. Насыщенные дуги потока (они выделены «жирными» линиями на рисунке) соответствуют ребрам наибольшего паросочетания исходного графа. Найденное наибольшее паросочетание не единственное.

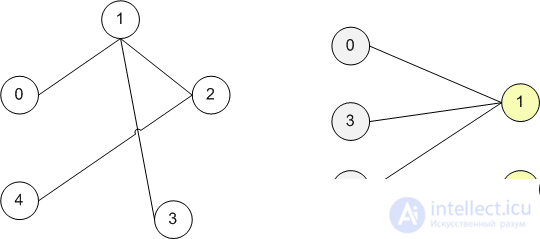
Найдем в исходном графе (слева) две доли и запомним их. Таким образом мы получим двудольный граф.

Добавим вершину-исток и вершину-сток. Соеденим исток и сток с разными долями графа.
Для всех ребер пропускная способность равна 1. Найдем максимальный поток из истока в сток.

Ребра первоначального графа, через которые поток равен 1, будут ребрами максимального паросочетания. В данном случае максимальное паросочетание состоит из 2 ребер: (0;1) и (2;4).

Найдем в исходном графе (слева) две доли и запомним их. Таким образом мы получим двудольный граф.

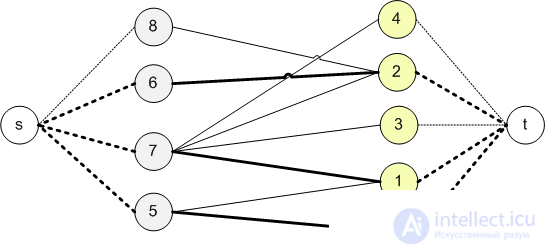
Добавим вершину-исток и вершину-сток. Соеденим исток и сток с разными долями графа.
Для всех ребер установим пропускную способность равную 1. Найдем максимальный поток из истока в сток.

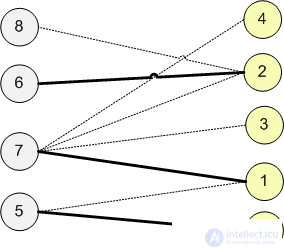
Ребра первоначального графа, через которые поток равен 1, будут ребрами максимального паросочетания. В данном случае максимальное паросочетание состоит из 2 ребер: (0;1) и (2;4).

На этом все! Теперь вы знаете все про поиск максимального паросочетания, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое поиск максимального паросочетания и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов