Лекция
Привет, сегодня поговорим про алгоритм дейкстры, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое алгоритм дейкстры, минимальное основное дерево , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
Алгоритм голландского ученого Эдсгера Дейкстры находит все кратчайшие пути из одной изначально заданной вершины графа до всех остальных. С его помощью, при наличии всей необходимой информации, можно, например, узнать какую последовательность дорог лучше использовать, чтобы добраться из одного города до каждого из многих других, или в какие страны выгодней экспортировать нефть и тому подобное. Минусом данного метода является невозможность обработки графов, в которых имеются ребра с отрицательным весом, т. е. если, например, некоторая система предусматривает убыточные для Вашей фирмы маршруты, то для работы с ней следует воспользоваться отличным от алгоритма Дейкстры методом.
алгоритм дейкстры — алгоритм на графах, изобретенный нидерландским ученым Э. Дейкстрой в 1959 году. Находит кратчайшее расстояние от одной из вершин графа до всех остальных. Алгоритм работает только для графов без ребер отрицательного веса.

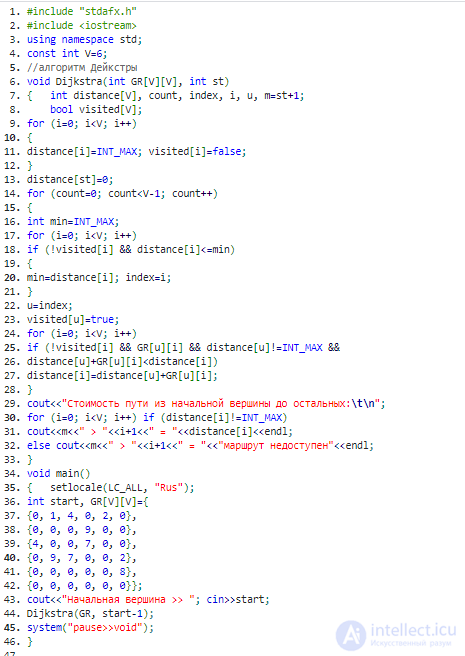
В строке 1 производится обычная инициализация величин d и pi, а в строке 2 инициализируется пустое множество вершин S. В этом алгоритме поддерживается инвариант, согласно которому в начале каждой итерации цикла while в строках 4-8 выполняется равенство Q = V — S. В строке 3 неубывающая очередь с приоритетами Q инициализируется таким образом, чтобы она содержала все вершины множества V; поскольку в этот момент S = 0, после выполнения строки 3 сформулированный выше инвариант выполняется . Об этом говорит сайт https://intellect.icu . При каждой итерации цикла while в строках 4-8 вершина и извлекается из множества Q = V — S и добавляется в множество 5, в результате чего инвариант продолжает соблюдаться. (Во время первой итерации этого цикла u = s.) Таким образом, вершина и имеет минимальную оценку кратчайшего пути среди всех вершин множества V — 5. Затем строках 7-8 ослабляются все ребра (u, v), исходящие из вершины и. Если текущий кратчайший путь к вершине v может быть улучшен в результате прохождения через вершину и, выполняется ослабление и соответствующее обновление оценки величины d [v] и предшественника тг [v]. Обратите внимание, что после выполнения строки 3 вершины никогда не добавляются в множество Q и что каждая вершина извлекается из этого множества и добавляется в множество 5 ровно по одному разу, поэтому количество итераций цикла while в строках 4-8 равно | V|. Поскольку в алгоритме Дейкстры из множества V — S для помещения в множество 5 всегда выбирается самая "легкая" или "близкая" вершина, говорят, что этот алгоритм придерживается жадной стратегии.
Время выполнения алгоритма Дейкстры зависит от реализации неубывающей очереди с приоритетами. Сначала рассмотрим случай, когда неубывающая очередь с приоритетами поддерживается за счет того, что все вершины пронумерованы от 1 до |V|. Атрибут d[v] просто помещается в элемент массива с индексом v. Каждая операция Insert и Decrease_Key (неявно присутствует в процедуре Relax) занимает время 0(1), а каждая операция Extract_Min — время О (V) (поскольку в ней производится поиск по всему массиву); в результате полное время работы алгоритма равно О (V2 + Е) = О(V2).
Если граф достаточно разреженный, в частности, если количество вершин и ребер в нем связаны соотношением Е = o(V2/lgV), с практической точки зрения целесообразно реализовать неубывающую очередь с приоритетами в виде бинарной неубывающей пирамиды. (важная деталь реализации заключается в том, что вершины и соответствующие им элементы пирамиды должны поддерживать идентификаторы друг друга.) Далее, каждая операция Extract_Min занимает время О (lg V), Как и раньше, таких операций |V|. Время, необходимое для построения неубывающей пирамиды, равно O(V). Каждая операция Decrease_Key занимает время O(lgV), и всего выполняется не более |Е| таких операций. Поэтому полное время выполнения алгоритма равно О ((V + Е) lg V), что равно О (Е*lg V), если все вершины достижимы из истока. Это время работы оказывается лучшим по сравнению со временем работы прямой реализации О (V2), если Е = о (V2/lg V).

Для программной реализации алгоритма понадобиться два массива: логический visited – для хранения информации о посещенных вершинах и численный distance, в который будут заноситься найденные кратчайшие пути. Об этом говорит сайт https://intellect.icu . Итак, имеется граф G=(V, E). Каждая из вершин входящих во множество V, изначально отмечена как не посещенная, т. е. элементам массива visited присвоено значение false. Поскольку самые выгодные пути только предстоит найти, в каждый элемент вектора distance записывается такое число, которое заведомо больше любого потенциального пути (обычно это число называют бесконечностью, но в программе используют, например максимальное значение конкретного типа данных). В качестве исходного пункта выбирается вершина s и ей приписывается нулевой путь: distance[s]=0, т. к. нет ребра из s в s (метод не предусматривает петель). Далее, находятся все соседние вершины (в которые есть ребро из s) [пусть таковыми будут t и u] и поочередно исследуются, а именно вычисляется стоимость маршрута из s поочередно в каждую из них:
Но вполне вероятно, что в ту или иную вершину из s существует несколько путей, поэтому цену пути в такую вершину в массиве distance придется пересматривать, тогда наибольшее (неоптимальное) значение игнорируется, а наименьшее ставиться в соответствие вершине.
После обработки смежных с s вершин она помечается как посещенная: visited[s]=true, и активной становится та вершина, путь из s в которую минимален. Допустим, путь из s в u короче, чем из s в t, следовательно, вершина u становиться активной и выше описанным образом исследуются ее соседи, за исключением вершины s. Далее, u помечается как пройденная: visited[u]=true, активной становится вершина t, и вся процедура повторяется для нее. Алгоритм Дейкстры продолжается до тех пор, пока все доступные из s вершины не будут исследованы.
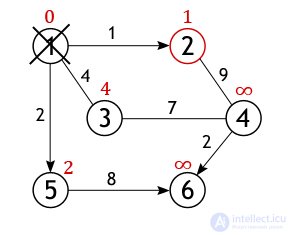
Теперь на конкретном графе проследим работу алгоритма, найдем все кратчайшие пути между истоковой и всеми остальными вершинами. Размер (количество ребер) изображенного ниже графа равен 7 (|E|=7), а порядок (количество вершин) – 6 (|V|=6). Это взвешенный граф, каждому из его ребер поставлено в соответствие некоторое числовое значение, поэтому ценность маршрута необязательно определяется числом ребер, лежащих между парой вершин.

Из всех вершин входящих во множество V выберем одну, ту, от которой необходимо найти кратчайшие пути до остальных доступных вершин. Пусть таковой будет вершина 1. Длина пути до всех вершин, кроме первой, изначально равна бесконечности, а до нее – 0, т. к. граф не имеет петель.

У вершины 1 ровно 3 соседа (вершины 2, 3, 5), и чтобы вычислить длину пути до них нужно сложить вес дуг, лежащих между вершинами: 1 и 2, 1 и 3, 1 и 5 со значением первой вершины (с нулем):
Как уже отмечалось, получившиеся значения присваиваются вершинам, лишь в том случае если они «лучше» (меньше) тех которые значатся на настоящий момент. А так как каждое из трех чисел меньше бесконечности, они становятся новыми величинами, определяющими длину пути из вершины 1 до вершин 2, 3 и 5.

Далее, активная вершина помечается как посещенная, статус «активной» (красный круг) переходит к одной из ее соседок, а именно к вершине 2, поскольку она ближайшая к ранее активной вершине.
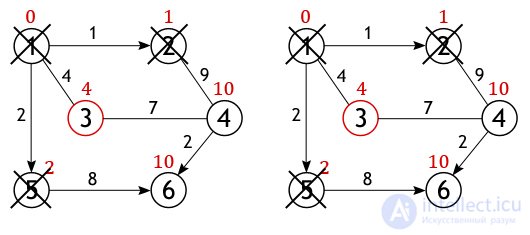
У вершины 2 всего один не рассмотренный сосед (вершина 1 помечена как посещенная), расстояние до которого из нее равно 9, но нам необходимо вычислить длину пути из истоковой вершины, для чего нужно сложить величину приписанную вершине 2 с весом дуги из нее в вершину 4:
Условие «краткости» (10<∞) выполняется, следовательно, вершина 4 получает новое значение длины пути.

Вершина 2 перестает быть активной, также как и вершина 1 удаляется из списка не посещенных. Теперь тем же способом исследуются соседи вершины 5, и вычисляется расстояние до них.
Когда дело доходит до осмотра соседей вершины 3, то тут важно не ошибиться, т. к. вершина 4 уже была исследована и расстояние одного из возможных путей из истока до нее вычислено. Если двигаться в нее через вершину 3, то путь составит 4+7=11, а 11>10, поэтому новое значение игнорируется, старое остается.
 Аналогичная ситуация с вершиной 6. Значение самого близкого пути до нее из вершины 1 равно 10, а оно получается только в том случае, если идти через вершину 5.
Аналогичная ситуация с вершиной 6. Значение самого близкого пути до нее из вершины 1 равно 10, а оно получается только в том случае, если идти через вершину 5.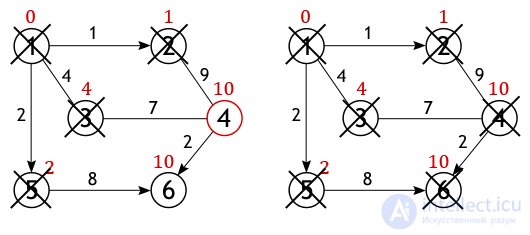 Когда все вершины графа, либо все те, что доступны из истока, будут помечены как посещенные, тогда работа алгоритма Дейкстры завершится, и все найденные пути будут кратчайшими. Так, например, будет выглядеть список самых оптимальных расстояний лежащих между вершиной 1 и всеми остальными вершинами, рассматриваемого графа:
Когда все вершины графа, либо все те, что доступны из истока, будут помечены как посещенные, тогда работа алгоритма Дейкстры завершится, и все найденные пути будут кратчайшими. Так, например, будет выглядеть список самых оптимальных расстояний лежащих между вершиной 1 и всеми остальными вершинами, рассматриваемого графа:
1→1=0
1→2=1
1→3=4
1→4=10
1→5=2
1→6=10
В программе, находящей ближайшие пути между вершинами посредством метода Дейкстры, граф будет представлен в виде не бинарной матрицы смежности. Вместо единиц в ней будут выставлены веса ребер, функция нулей останется прежней: показывать, между какими вершинами нет ребер или же они есть, но отрицательно направленны.

|
Алгоритмы поиска на графах
|
|
|---|---|
| Неинформированные методы |
|
| Информированные методы |
|
| Кратчайшие пути |
|
| Минимальное остовное дерево | |
| Другое |
|
На этом все! Теперь вы знаете все про алгоритм дейкстры, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое алгоритм дейкстры, минимальное основное дерево и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов