Лекция
Сразу хочу сказать, что здесь никакой воды про алгоритм, и только нужная информация. Для того чтобы лучше понимать что такое алгоритм, исполнители алгоритмов, блок-схема, виды алгоритмов , анализ алгоритмов , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
алгоритм (лат. algorithmi — от арабского имени математика Аль-Хорезми ) — это конечная совокупность точно заданных правил решения произвольного класса задач или набор инструкций, описывающих порядок действий исполнителя для решения некоторой задачи. В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Независимые инструкции могут выполняться в произвольном порядке, параллельно, если это позволяют используемые исполнители.
Ранее в русском языке писали «алгорифм», сейчас такое написание используется редко, но тем не менее имеет место исключение (нормальный алгорифм Маркова).
Мета-алгоритм(Метаалгоритм) это обобщение понятия алгоритма. Классические формализации понятия алгоритма (например, нормальные алгоритмы) не в полной мере обеспечивают надлежащую формализацию интуитивного понятия алгоритма. Нормальные алгоритмы, например, не обеспечивают однозначное применение нормального алгоритма к себе (так как для применения алгоритма к схеме алгоритма требуется преобразование схемы алгоритма в некоторое слово в используемом алфавите, которое может быть осуществлено лишь «вручную», на основе некоторых договоренностей; поскольку договоренности являются не более, чем договоренностями (соглашениями), они могут меняться, что влечет неоднозначность применения алгоритма к себе). Некоторая модификация нормальных алгоритмов обеспечивает однозначное применение самих себя к себе. Такая формализация понятия алгоритма считается определением мета-алгоритма
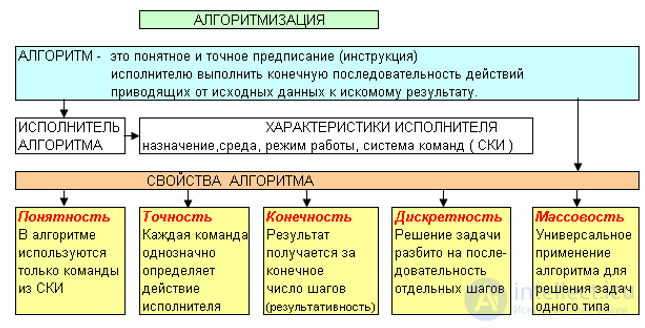
Часто в качестве исполнителя выступает компьютер, но понятие алгоритма необязательно относится к компьютерным программам, так, например, четко описанный рецепт приготовления блюда также является алгоритмом, в таком случае исполнителем является человек (а может быть и некоторый механизм, ткацкий станок, и пр.).
Можно выделить алгоритмы вычислительные (далее речь в основном идет о них), и управляющие. Вычислительные по сути преобразуют некоторые начальные данные в выходные, реализуя вычисление некоторой функции. Семантика управляющих алгоритмов существенным образом может отличаться и сводиться к выдаче необходимых управляющих воздействий либо в заданные моменты времени, либо в качестве реакции на внешние события (в этом случае, в отличие от вычислительного алгоритма, управляющий может оставаться корректным при бесконечном выполнении).
Понятие алгоритма относится к первоначальным, основным, базисным понятиям математики. Вычислительные процессы алгоритмического характера (арифметические действия над целыми числами, нахождение наибольшего общего делителя двух чисел и т. д.) известны человечеству с глубокой древности. Однако в явном виде понятие алгоритма сформировалось лишь в начале XX века.
Частичная формализация понятия алгоритма началась с попыток решения проблемы разрешения (нем. Entscheidungsproblem), которую сформулировал Давид Гильберт в 1928 году. Следующие этапы формализации были необходимы для определения эффективных вычислений или «эффективного метода» ; среди таких формализаций — рекурсивные функции Геделя — Эрбрана — Клини 1930, 1934 и 1935 гг., λ-исчисление Алонзо Черча 1936 г., «Формулировка 1» Эмиля Поста 1936 года и машина Тьюринга.
" Мы редко до конца понимаем, чего мы в действительности хотим. "
Франсуа де Ларошфуко
" Алгоритм должен быть определен настолько четко, чтобы его указаниям мог следовать даже компьютер. "
Дональд Э. Кнут
Максима герцога Ларошфуко, приведенная выше, заставляет быть осторожным в попытке коротко охарактеризовать предлагаемый вашему вниманию курс. Как его назвать?
Круг тем, к которым нам предстоит обратиться, многочисленные учебники относят к таким разделам науки, как теоретическая информатика, конечная математика, дискретная математика и другим. Авторитет "Математической энциклопедии" (М., 1977-1985) не помогает: проблемы классификации после обращения к ее словарным статьям остаются. Как ни странно, эти статьи - на близкие по содержанию темы - написаны разными специалистами, не согласовавшими свои трактовки определяемых понятий.
Не найдя ожидаемой поддержки, автор рисковал оказаться почти в положении американского логика Реймонда Смаллиана (Raymond M. Smullyan), так и не придумавшего названия своей известной книги. Все же помощь пришла - со стороны двух французов, Патрика Нодена (Patrice Naudin) и Клода Китте (Claude Quitte). После счастливого знакомства с написанным ими толстенным томом "Алгебраическая алгоритмика" (М., 1999) никакие подобные словосочетания уже не кажутся слишком смелыми. Так что предлагаю читателю рассматривать наш курс как введение в компьютерную алгоритмику.
Предметом обсуждения, разумеется, станут алгоритмы, и удобно было бы начать с формального определения этого понятия. Но сделать это отнюдь не просто: нужно вникать в содержание весьма нетривиальной теории алгоритмов, а ее к вводному курсу уж никак не отнести.
Можно ли обойтись без определения, рассчитывая лишь на интуитивное представление читателя о сущности алгоритма? Пожалуй, настораживает излишняя популярность интересующего нас термина и, как в таких случаях говорят, его расширительное толкование. Так, автору попадались "алгоритм шахматиста" (в книге), "алгоритм сбора информации" при социологическом опросе (в газетной публикации) и прочие.
Поэтому возьмем за основу представление об алгоритме как описании некоторого вычислительного процесса, а далее введем некоторые уточнения. Тем не менее, иллюстрацией нам часто будут служить примеры невычислительного характера, не связанные напрямую с компьютерной обработкой информации, за что читатель, надеюсь, нас не осудит.
Сначала - уточнения терминологические. Нередко, в целях экономии, сочетание "описание вычислительного процесса" мы будем заменять коротким "процесс", что не должно вводить читателя в заблуждение. В самом деле, мы чаще будем только конструировать алгоритмы, вовсе не стремясь тут же их применить. Кроме того, если алгоритм - это описание процесса, то способ представления алгоритма - это "описание описания процесса". Половину "описаний" так и хочется отбросить.
Итак, условимся, что форма записи алгоритма - формат и его содержание - отнюдь не произвольны, а подчинены вполне определенным ограничениям.
Начнем с форматов записи, коих известно немало. Читатель, знакомый с технологией программирования, следует при записи алгоритма достаточно жестким правилам конкретного языка, - безразлично, какого. Вполне вероятно, что первые его уроки были посвящены языку блок-схем. Другую разновидность языка схем представляют весьма компактные диаграммы Насси-Шнейдермана. Оба графических формата обладают как достоинствами, так и недостатками, но здесь нет места их обсуждению. Общей же для всех графических форматов является возможность либо помещать текст описания внутрь блоков, либо выносить комментарий за пределы рисунка.
При всем многообразии способов записи алгоритма мы отдаем предпочтение "первичной" форме, а именно, словесному описанию. Разумеется, в этом варианте также прибегают к ряду обозначений, обычно вполне очевидных, в частности, - явной нумерации шагов. Альтернативой излишней краткости могут стать дополнительные комментарии.
Страница из «Алгебры» аль-Хорезми — хорезмского математика, от имени которого происходит слово алгоритм.
Аль-Хорезми на советской марке
Современное формальное определение вычислительного алгоритма было дано в 30—50-е годы XX века в работах Тьюринга, Поста, Черча (тезис Черча — Тьюринга), Н. Винера, А. А. Маркова.
Само слово «алгоритм» происходит от имени хорезмского ученого аль-Хорезми. Около 825 года он написал сочинение Китаб аль-джебр валь-мукабала («Книга о сложении и вычитании»), из оригинального названия которого происходит слово «алгебра» (аль-джебр — восполнение). В этой книге впервые дал описание придуманной в Индии позиционной десятичной системы счисления. Персидский оригинал книги не сохранился. Аль-Хорезми сформулировал правила вычислений в новой системе и, вероятно, впервые использовал цифру 0 для обозначения пропущенной позиции в записи числа (ее индийское название арабы перевели как as-sifr или просто sifr, отсюда такие слова, как «цифра» и «шифр»). Приблизительно в это же время индийские цифры начали применять и другие арабские ученые.
В первой половине XII века книга аль-Хорезми в латинском переводе проникла в Европу. Переводчик, имя которого до нас не дошло, дал ей название Algoritmi de numero Indorum («Алгоритми о счете индийском») — таким образом, латинизированное имя среднеазиатского ученого было вынесено в заглавие книги. Сегодня считается, что слово «алгоритм» попало в европейские языки именно благодаря этому переводу. В течение нескольких следующих столетий появилось множество других трудов, посвященных все тому же вопросу — обучению искусству счета с помощью цифр, и все они имели в названии слово algoritmi или algorismi.
Про аль-Хорезми позднейшие авторы ничего не знали, но поскольку первый перевод книги начинается словами: «Dixit algorizmi: …» («Аль-Хорезми говорил: …»), все еще связывали это слово с именем конкретного человека. Очень распространенной была версия о греческом происхождении книги. В англо-норманнской рукописи XIII века, написанной в стихах, читаем:
Алгоризм был придуман в Греции.
Это часть арифметики. Придуман он был мастером по имени Алгоризм, который дал ему свое имя. И поскольку его звали Алгоризм,
Он назвал свою книгу «Алгоризм».
Около 1250 года английский астроном и математик Иоанн Сакробоско написал труд по арифметике Algorismus vulgaris, на столетия ставший основным учебником по вычислениям в десятичной позиционной системе счисления во многих европейских университетах. Во введении Сакробоско назвал автором науки о счете мудреца по имени Алгус (Algus). А в популярной средневековой поэме «Роман о Розе» (1275—1280) Жана де Мена «греческий философ Алгус» ставится в один ряд с Платоном, Аристотелем, Евклидом и Птолемеем! Встречался также вариант написания имени Аргус (Argus). И хотя, согласно древнегреческой мифологии, корабль «Арго» был построен Ясоном, именно этому Арго приписывалось строительство корабля.
«Мастер Алгус» (или Аргус) стал в средневековой литературе олицетворением счетного искусства. И в уже упоминавшейся «Романе о розе», и в известной итальянской поэме «Цветок», написанной Дуранте, имеются фрагменты, в которых говорится, что даже «mestre Argus» не сумеет подсчитать, сколько раз ссорятся и мирятся влюбленные. Английский поэт Джефри Чосер в поэме «Книга герцогини» (1369 г.) пишет, что даже «славный счетчик Аргус» (noble countour Argu) не сможет счесть чудовищ, явившихся в кошмарных видениях герою.
Баронесса Ада Лавлейс, которую считают первым программистом.
Однако со временем такие объяснения все менее занимали математиков, и слово algorism (или algorismus), неизменно присутствовавшее в названиях математических сочинений, обрело значение способа выполнения арифметических действий посредством арабских цифр, то есть на бумаге, без использования абака. Именно в таком значении оно вошло во многие европейские языки. Например, с пометкой «устар.» оно присутствует в представительном словаре английского языка Webster’s New World Dictionary, изданном в 1957 г. Энциклопедический словарь Брокгауза и Ефрона предлагает такую трактовку: алгорифм (кстати, до революции использовалось написание алгориѳм, через фиту) производится «от арабского слова Аль-Горетм, то есть корень».
Алгоритм — это искусство счета с помощью цифр, но поначалу слово «цифра» относилось только к нулю. Знаменитый французский трувер Готье де Куанси (Gautier de Coincy, 1177—1236) в одном из стихотворений использовал слова algorismus-cipher (которые означали цифру 0) как метафору для характеристики абсолютно никчемного человека. Очевидно, понимание такого образа требовало соответствующей подготовки слушателей, а это означает, что новая система счисления уже была им достаточно хорошо известна.
Многие века абак был фактически единственным средством для практичных вычислений, им пользовались и купцы, и менялы, и ученые. Достоинства вычислений на счетной доске разъяснял в своих сочинениях такой выдающийся мыслитель, как Герберт Аврилакский (938—1003), ставший в 999 г. папой римским под именем Сильвестра II. Новое с огромным трудом пробивало себе дорогу, и в историю математики вошло упорное противостояние лагерей алгорисмиков и абацистов (иногда называемых гербекистами), которые пропагандировали использование для вычислений абака вместо арабских цифр. Интересно, что известный французский математик Николя Шюке (Nicolas Chuquet, 1445—1488) в реестр налогоплательщиков города Лиона был вписан как алгорисмик (algoriste). Но прошло не одно столетие, прежде чем новый способ счета окончательно утвердился, столько времени потребовалось, чтобы выработать общепризнанные обозначения, усовершенствовать и приспособить к записи на бумаге методы вычислений. В Западной Европе учителей арифметики вплоть до XVII века продолжали называть «магистрами абака», как, например, математика Никколо Тарталью (1500—1557).
Итак, сочинения по искусству счета назывались Алгоритмами. Из многих сотен можно выделить и такие необычные, как написанный в стихах трактат Carmen de Algorismo (латинское carmen и означает стихи) Александра де Вилла Деи (Alexander de Villa Dei, ум. 1240) или учебник венского астронома и математика Георга Пурбаха (Georg Peurbach, 1423—1461) Opus algorismi jocundissimi («Веселейшее сочинение по алгоритму»).
Постепенно значение слова расширялось. Ученые начинали применять его не только к сугубо вычислительным, но и к другим математическим процедурам. Например, около 1360 г. французский философ Николай Орем (Nicolaus Oresme, 1323/25-1382) написал математический трактат Algorismus proportionum («Вычисление пропорций»), в котором впервые использовал степени с дробными показателями и фактически вплотную подошел к идее логарифмов. Когда же на смену абаку пришел так называемый счет на линиях, многочисленные руководства по нему стали называть Algorithmus linealis, то есть правила счета на линиях.
Можно обратить внимание на то, что первоначальная форма algorismi спустя какое-то время потеряла последнюю букву, и слово приобрело более удобное для европейского произношения вид algorism. Позднее и оно, в свою очередь, подверглось искажению, скорее всего, связанному со словом arithmetic.
В 1684 году Готфрид Лейбниц в сочинении Nova Methodvs pro maximis et minimis, itemque tangentibus… впервые использовал слово «алгоритм» (Algorithmo) в еще более широком смысле: как систематический способ решения проблем дифференциального исчисления.
В XVIII веке в одном из германских математических словарей, Vollstandiges mathematisches Lexicon (изданном в Лейпциге в 1747 г.), термин algorithmus все еще объясняется как понятие о четырех арифметических операциях. Но такое значение не было единственным, ведь терминология математической науки в те времена еще только формировалась. В частности, выражение algorithmus infinitesimalis применялось к способам выполнения действий с бесконечно малыми величинами. Пользовался словом алгоритм и Леонард Эйлер, одна из работ которого так и называется — «Использование нового алгоритма для решения проблемы Пелля» (De usu novi algorithmi in problemate Pelliano solvendo). Мы видим, что понимание Эйлером алгоритма как синонима способа решения задачи уже очень близко к современному.
Однако потребовалось еще почти два столетия, чтобы все старинные значения слова вышли из употребления. Этот процесс можно проследить на примере проникновения слова «алгоритм» в русский язык.
Историки датируют 1691 годом один из списков древнерусского учебника арифметики, известного как «Счетная мудрость». Это сочинение известно во многих вариантах (самые ранние из них почти на сто лет старше) и восходит к еще более древним рукописям XVI в. По ним можно проследить, как знание арабских цифр и правил действий с ними постепенно распространялось на Руси. Полное название этого учебника — «Сия книга, глаголемая по-еллински и по-гречески арифметика, а по-немецки алгоризма, а по-русски цифирная счетная мудрость».
Таким образом, слово «алгоритм» понималось первыми русскими математиками так же, как и в Западной Европе. Однако его не было ни в знаменитом словаре В. И. Даля, ни спустя сто лет в «Толковом словаре русского языка» под редакцией Д. Н. Ушакова (1935 г.). Зато слово «алгорифм» можно найти и в популярном дореволюционном Энциклопедическом словаре братьев Гранат, и в первом издании Большой советской энциклопедии (БСЭ), изданном в 1926 г. И там, и там оно трактуется одинаково: как правило, по которому выполняется то или иное из четырех арифметических действий в десятичной системе счисления. Однако к началу XX в. для математиков слово «алгоритм» уже означало любой арифметический или алгебраический процесс, выполняемый по строго определенным правилам, и это объяснение также дается в следующих изданиях БСЭ.
Алгоритмы становились предметом все более пристального внимания ученых, и постепенно это понятие заняло одно из центральных мест в современной математике. Что же касается людей, от математики далеких, то к началу сороковых годов это слово они могли услышать разве что во время учебы в школе, в сочетании «алгоритм Евклида». Несмотря на это, алгоритм все еще воспринимался как термин сугубо специальный, что подтверждается отсутствием соответствующих статей в менее объемных изданиях. В частности, его нет даже в десятитомной Малой советской энциклопедии (1957 г.), не говоря уже об однотомных энциклопедических словарях. Но зато спустя десять лет, в третьем издании Большой советской энциклопедии (1969 г.) алгоритм уже характеризуется как одна из основных категорий математики, «не обладающих формальным определением в терминах более простых понятий, и абстрагируемых непосредственно из опыта». Об этом говорит сайт https://intellect.icu . Как мы видим, отличие даже от трактовки первым изданием БСЭ разительное! За сорок лет алгоритм превратился в одно из ключевых понятий математики, и признанием этого стало включение слова уже не в энциклопедии, а в словари. Например, оно присутствует в академическом «Словаре русского языка» (1981 г.) именно как термин из области математики.
Одновременно с развитием понятия алгоритма постепенно происходила и его экспансия из чистой математики в другие сферы. И начало ей положило появление компьютеров, благодаря которому слово «алгоритм» вошло в 1985 г. во все школьные учебники информатики и обрело новую жизнь. Вообще можно сказать, что его сегодняшняя известность напрямую связана со степенью распространения компьютеров. Например, в третьем томе «Детской энциклопедии» (1959 г.) о вычислительных машинах говорится немало, но они еще не стали чем-то привычным и воспринимаются скорее как некий атрибут светлого, но достаточно далекого будущего. Соответственно и алгоритмы ни разу не упоминаются на ее страницах. Но уже в начале 70-х гг. прошлого столетия, когда компьютеры перестали быть экзотической диковинкой, слово «алгоритм» стремительно входит в обиход. Это чутко фиксируют энциклопедические издания. В «Энциклопедии кибернетики» (1974 г.) в статье «Алгоритм» он уже связывается с реализацией на вычислительных машинах, а в «Советской военной энциклопедии» (1976 г.) даже появляется отдельная статья «Алгоритм решения задачи на ЭВМ». За последние полтора-два десятилетия компьютер стал неотъемлемым атрибутом нашей жизни, компьютерная лексика становится все более привычной. Слово «алгоритм» в наши дни известно, вероятно, каждому. Оно уверенно шагнуло даже в разговорную речь, и сегодня мы нередко встречаем в газетах и слышим в выступлениях политиков выражения вроде «алгоритм поведения», «алгоритм успеха» или даже «алгоритм предательства». Академик Н. Н. Моисеев назвал свою книгу «Алгоритмы развития», а известный врач Н. М. Амосов — «Алгоритм здоровья» и «Алгоритмы разума». А это означает, что слово живет, обогащаясь все новыми значениями и смысловыми оттенками.
Различные определения алгоритма в явной или неявной форме содержат следующий ряд общих требований:
Разнообразные теоретические проблемы математики и ускорение развития физики и техники поставили на повестку дня точное определение понятия алгоритма.
Первые попытки уточнения понятия алгоритма и его исследования осуществляли в первой половине XX века Алан Тьюринг, Эмиль Пост, Жак Эрбран, Курт Гедель, А. А. Марков, Алонзо Черч. Было разработано несколько определений понятия алгоритма, но впоследствии было выяснено, что все они определяют одно и то же понятие (см. Тезис Черча — Тьюринга)
Российский математик, основоположник структурной лингвистики в Советском Союзе В. А. Успенский считал, что понятие алгоритма впервые появилось у Эмиля Бореля в 1912 году, в статье об определенном интеграле. Там он написал о «вычислениях, которые можно реально осуществить», подчеркивая при этом: «Я намеренно оставляю в стороне большую или меньшую практическую деятельность; суть здесь та, что каждая из этих операций осуществима в конечное время при помощи достоверного и недвусмысленного метода» .
Машина Тьюринга
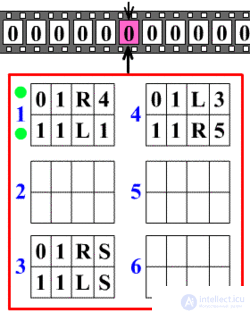
Схематическая иллюстрация работы машины Тьюринга.
Основная идея, лежащая в основе машины Тьюринга, очень проста. Машина Тьюринга — это абстрактная машина (автомат), работающая с лентой отдельных ячеек, в которых записаны символы. Машина также имеет головку для записи и чтения символов из ячеек, которая может двигаться вдоль ленты. На каждом шаге машина считывает символ из ячейки, на которую указывает головка, и, на основе считанного символа и внутреннего состояния, делает следующий шаг. При этом машина может изменить свое состояние, записать другой символ в ячейку или передвинуть головку на одну ячейку вправо или влево.
На основе исследования этих машин был выдвинут тезис Тьюринга (основная гипотеза алгоритмов):
 |
Некоторый алгоритм для нахождения значений функции, заданной в некотором алфавите, существует тогда и только тогда, когда функция исчисляется по Тьюрингу, то есть когда ее можно вычислить на машине Тьюринга. |  |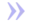
Этот тезис является аксиомой, постулатом, и не может быть доказан математическими методами, поскольку алгоритм не является точным математическим понятием.
Рекурсивные функции
С каждым алгоритмом можно сопоставить функцию, которую он вычисляет. Однако возникает вопрос, можно ли произвольной функции сопоставить машину Тьюринга, а если нет, то для каких функций существует алгоритм? Исследования этих вопросов привели к созданию в 1930-х годах теории рекурсивных функций .
Класс вычислимых функций был записан в образ, напоминающий построение некоторой аксиоматической теории на базе системы аксиом. Сначала были выбраны простейшие функции, вычисление которых очевидно. Затем были сформулированы правила (операторы) построения новых функций на основе уже существующих. Необходимый класс функций состоит из всех функций, которые можно получить из простейших применением операторов.
Подобно тезису Тьюринга в теории вычислимых функций была выдвинута гипотеза, которая называется тезис Черча:
|
Числовая функция тогда и только тогда алгоритмически исчисляется, когда она частично рекурсивна. | |
Доказательство того, что класс вычислимых функций совпадает с исчисляемыми по Тьюрингу, происходит в два шага: сначала доказывают вычисление простейших функций на машине Тьюринга, а затем — вычисление функций, полученных в результате применения операторов.
Таким образом, неформально алгоритм можно определить как четкую систему инструкций, определяющих дискретный детерминированный процесс, который ведет от начальных данных (на входе) к искомому результату (на выходе), если он существует, за конечное число шагов; если искомого результата не существует, алгоритм или никогда не завершает работу, либо заходит в тупик.
Нормальный алгоритм Маркова
Нормальный алгоритм Маркова — это система последовательных применений подстановок, которые реализуют определенные процедуры получения новых слов из базовых, построенных из символов некоторого алфавита. Как и машина Тьюринга, нормальные алгоритмы не выполняют самих вычислений: они лишь выполняют преобразование слов путем замены букв по заданным правилам[10].
Нормально вычислимой называют функцию, которую можно реализовать нормальным алгоритмом. То есть алгоритмом, который каждое слово из множества допустимых данных функции превращает в ее начальные значения[11]..
Создатель теории нормальных алгоритмов А. А. Марков выдвинул гипотезу, которая получила название принцип нормализации Маркова:
|
Для нахождения значений функции, заданной в некотором алфавите, тогда и только тогда существует некоторый алгоритм, когда функция нормально исчисляемая. | |
Подобно тезисам Тьюринга и Черча, принцип нормализации Маркова не может быть доказан математическими средствами.
Однако приведенное выше формальное определение алгоритма в некоторых случаях может быть слишком строгим. Иногда возникает потребность в использовании случайных величин[12]. Алгоритм, работа которого определяется не только исходными данными, но и значениями, полученными из генератора случайных чисел, называют стохастическим (или рандомизированным, от англ. randomized algorithm)[13]. Стохастические алгоритмы часто бывают эффективнее детерминированных, а в отдельных случаях — единственным способом решить задачу[12].
На практике вместо генератора случайных чисел используют генератор псевдослучайных чисел.
Однако следует отличать стохастические алгоритмы и методы, которые дают с высокой вероятностью правильный результат. В отличие от метода, алгоритм дает корректные результаты даже после продолжительной работы.
Некоторые исследователи допускают возможность того, что стохастический алгоритм даст с некоторой заранее известной вероятностью неправильный результат. Тогда стохастические алгоритмы можно разделить на два типа[14]:
Для некоторых задач названные выше формализации могут затруднять поиск решений и осуществление исследований. Для преодоления препятствий были разработаны как модификации «классических» схем, так и созданы новые модели алгоритма. В частности, можно назвать:
и другие.
Виды алгоритмов как логико-математических средств отражают указанные компоненты человеческой деятельности и тенденции, а сами алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения. Следует подчеркнуть принципиальную разницу между алгоритмами вычислительного характера, преобразующими некоторые входные данные в выходные (именно их формализацией являются упомянутые выше машины Тьюринга, Поста, РАМ, нормальные алгорифмы Маркова и рекурсивные функции), и интерактивными алгоритмами (уже у Тьюринга встречается C-машина, от англ. choice — выбор, ожидающая внешнего воздействия, в отличие от классической A-машины, где все начальные данные заданы до начала вычисления и выходные данные недоступны до окончания вычисления). Последние предназначены для взаимодействия с некоторым объектом управления и призваны обеспечить корректную выдачу управляющих воздействий в зависимости от складывающейся ситуации, отражаемой поступающими от объекта управления сигналами[15][16]. В некоторых случаях алгоритм управления вообще не предусматривает окончания работы (например, поддерживает бесконечный цикл ожидания событий, на которые выдается соответствующая реакция), несмотря на это, являясь полностью правильным.
Можно также выделить алгоритмы:
продолжение следует...
Часть 1 Алгоритм: понятие, терминология, свойства, запись
Часть 2 Нумерация алгоритмов - Алгоритм: понятие, терминология, свойства, запись
А как ты думаешь, при улучшении алгоритм, будет лучше нам? Надеюсь, что теперь ты понял что такое алгоритм, исполнители алгоритмов, блок-схема, виды алгоритмов , анализ алгоритмов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов