Лекция
Это окончание невероятной информации про алгоритм.
...
детерминированные, жесткие (например, алгоритм работы машины, двигателя и т. п.) — задают определенные действия, обозначая их в единственной и достоверной последовательности, обеспечивая тем самым однозначный требуемый или искомый результат, если выполняются те условия процесса, задачи, для которых разработан алгоритм.Нумерация алгоритмов играет важную роль в их исследовании и анализе[18]. Поскольку любой алгоритм можно задать в виде конечного слова (представить в виде конечной последовательности символов некоторого алфавита), а множество всех конечных слов в конечном алфавите счетное, то множество всех алгоритмов также счетное. Это означает существование взаимно однозначного отображения между множеством натуральных чисел и множеством алгоритмов, то есть возможность присвоить каждому алгоритму номер.
Нумерация алгоритмов является одновременно и нумерацией всех алгоритмически исчисляемых функций, причем любая функция может иметь бесконечное количество номеров.
Существование нумерации позволяет работать с алгоритмами так же, как с числами. Особенно полезна нумерация в исследовании алгоритмов, работающих с другими алгоритмами.
Формализация понятия алгоритма позволила исследовать существование задач, для которых не существует алгоритмов поиска решений. Впоследствии была доказана невозможность алгоритмического вычисления решений ряда задач, что делает невозможным их решение на любом вычислительном устройстве. Функцию называют вычислимой (англ. computable), если существует машина Тьюринга, которая вычисляет значение {\displaystyle f}
для всех элементов множества определения функции. Если такой машины не существует, функцию {\displaystyle f}
называют невычислимой. Функция будет считаться невычислимой, даже если существуют машины Тьюринга, способные вычислить значение для подмножества из всего множества входных данных[19].
Случай, когда результатом вычисления функции является логическое выражение «истина» или «ложь» (или множество {0, 1}), называют задачей, которая может быть решаемой или нерешаемой, в зависимости от вычислимости функции
Важно точно указывать допустимое множество входных данных, поскольку задача может быть решаемой для одного множества и нерешаемой для другого.
Одной из первых задач, для которой была доказана нерешаемость, является проблема остановки. Формулируется она следующим образом:
Имея описание программы для машины Тьюринга, требуется определить, завершит ли работу программа за конечное время или будет работать бесконечно, получив некоторые входные данные
Доказательство неразрешимости проблемы остановки важно тем, что к ней можно свести другие задачи. Например, простую проблему остановки можно свести к задаче остановки на пустой строке (когда нужно определить для заданной машины Тьюринга, остановится ли она, будучи запущенной на пустой строке), доказав тем самым неразрешимость последней
Вместе с распространением информационных технологий увеличился риск программных сбоев. Одним из способов избежания ошибок в алгоритмах и их реализациях служат доказательства корректности систем математическими средствами.
Использование математического аппарата для анализа алгоритмов и их реализаций называют формальными методами. Формальные методы предусматривают применение формальных спецификаций и, обычно, набора инструментов для синтаксического анализа и доказательства свойств спецификаций. Абстрагирование от деталей реализации позволяет установить свойства системы независимо от ее реализации. Кроме того, точность и однозначность математических утверждений позволяет избежать многозначности и неточности естественных языков[21].
По гипотезе Ричарда Мейса, «избежание ошибок лучше устранения ошибок»[22]. По гипотезе Хоара, «доказательство программ решает проблему корректности, документации и совместимости»[23]. Доказательство корректности программ позволяет выявлять их свойства по отношению ко всему диапазону входных данных. Для этого понятие корректности было разделено на два типа:
Во время доказательства корректности сравнивают текст программы со спецификацией желаемого соотношения входных-выходных данных. Для доказательств типа Хоара эта спецификация имеет вид утверждений, которые называют предусловиями и постусловиями. В совокупности с самой программой их еще называют тройкой Хоара. Эти утверждения записывают
P{Q}R
где P — это предусловие, что должно выполняться перед запуском программы Q, а R — постусловие, правильное после завершения работы программы.
Формальные методы были успешно применены для широкого круга задач, в частности: разработке электронных схем, искусственного интеллекта, автоматических систем на железной дороге, верификации микропроцессоров, спецификации стандартов и спецификации и верификации программ[24].
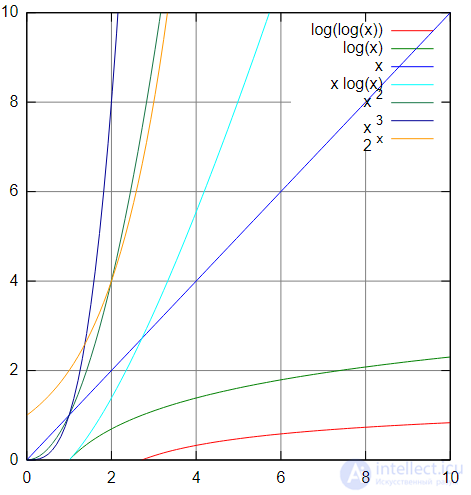
Графики функций, приведенных в таблице ниже.
Распространенным критерием оценки алгоритмов является время работы и порядок роста продолжительности работы в зависимости от объема входных данных.
Для каждой конкретной задачи составляют некоторое число, которое называют ее размером. Например, размером задачи вычисления произведения матриц может быть наибольший размер матриц-множителей, для задач на графах размером может быть количество ребер графа.
Время, которое тратит алгоритм как функция от размера задачи }, называют временной сложностью этого алгоритма T(n). Асимптотику поведения этой функции при увеличении размера задачи называют асимптотичной временной сложностью, а для ее обозначения используют нотацию «O» большое. Например, если алгоритм обрабатывает входные данные размером
за время cn², где c — некоторая константа, то говорят, что временная сложность такого алгоритма O(n²).
Асимптотическая сложность важна тем, что является характеристикой алгоритма, а не его конкретной реализации: «оптимизацией» операций, без замены алгоритма, можно изменить только мультипликативный коэффициент c, но не асимптотику. Как правило, именно асимптотическая сложность является главным фактором, который определяет размер задач, которые алгоритм способен обработать.
Часто во время разработки алгоритма пытаются уменьшить асимптотическую временную сложность для наихудших случаев. На практике же бывают случаи, когда достаточным является алгоритм, который «обычно» работает быстро.
Грубо говоря, анализ средней асимптотической временной сложности можно разделить на два типа: аналитический и статистический. Аналитический метод дает более точные результаты, но сложен в использовании на практике. Зато статистический метод позволяет быстрее осуществлять анализ сложных задач[26].
В следующей таблице приведены распространенные асимптотические сложности с комментариями[27].
| Сложность | Комментарий | Примеры |
|---|---|---|
| O(1) | Устойчивое время работы не зависит от размера задачи | Ожидаемое время поиска в хеш-таблице |
| O(log log n) | Очень медленный рост необходимого времени | Ожидаемое время работы интерполирующего поиска n элементов |
| O(log n) | Логарифмический рост — удвоение размера задачи увеличивает время работы на постоянную величину | Вычисление xn; Двоичный поиск в массиве из n элементов |
| O(n) | Линейный рост — удвоение размера задачи удвоит и необходимое время | Сложение/вычитание чисел из n цифр; Линейный поиск в массиве из n элементов |
| O(n log n) | Линеаритмичный рост — удвоение размера задачи увеличит необходимое время чуть более, чем вдвое | Сортировка слиянием или кучей n элементов; нижняя граница сортировки сопоставлением n элементов |
| O(n²) | Квадратичный рост — удвоение размера задачи увеличивает необходимое время в четыре раза | Элементарные алгоритмы сортировки |
| O(n³) | Кубичный рост — удвоение размера задачи увеличивает необходимое время в восемь раз | Обычное умножение матриц |
| O(cn) | Экспоненциальный рост — увеличение размера задачи на 1 приводит к c-кратному увеличению необходимого времени; удвоение размера задачи увеличивает необходимое время в квадрат | Некоторые задачи коммивояжера, алгоритмы поиска полным перебором |
Алгоритм — это точно определенная инструкция, последовательно применяя которую к исходным данным, можно получить решение задачи. Для каждого алгоритма есть некоторое множество объектов, допустимых в качестве исходных данных. Например, в алгоритме деления вещественных чисел делимое может быть любым, а делитель не может быть равен нулю.
Алгоритм служит, как правило, для решения не одной конкретной задачи, а некоторого класса задач. Так, алгоритм сложения применим к любой паре натуральных чисел. В этом выражается его свойство массовости, то есть возможности применять многократно один и тот же алгоритм для любой задачи одного класса.
Для разработки алгоритмов и программ используется алгоритмизация — процесс систематического составления алгоритмов для решения поставленных прикладных задач. Алгоритмизация считается обязательным этапом в процессе разработки программ и решении задач на ЭВМ. Именно для прикладных алгоритмов и программ принципиально важны детерминированность, результативность и массовость, а также правильность результатов решения поставленных задач.
Алгоритм — это понятное и точное предписание исполнителю совершить последовательность действий, направленных на достижение цели.
Формы записи алгоритма:
Обычно сначала (на уровне идеи) алгоритм описывается словами, но по мере приближения к реализации он обретает все более формальные очертания и формулировку на языке, понятном исполнителю (например, машинный код).
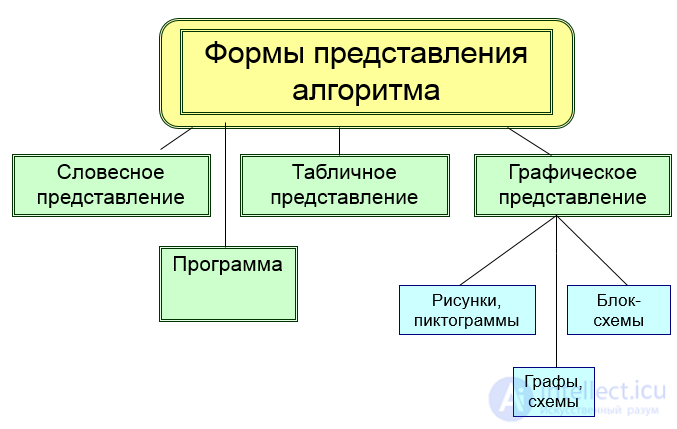
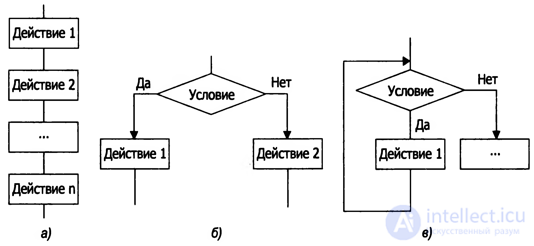
Рисунок . формы записи алгоритмов
Граф — геометрический объект, состоящий из вершин и соединяющих вершины линий-дуг. В алгоритме анализа структуры предложения вершинами являются члены предложения, дуги показывают связи членов предложения, направления дуг — последовательность анализа (порядок действий алгоритма).
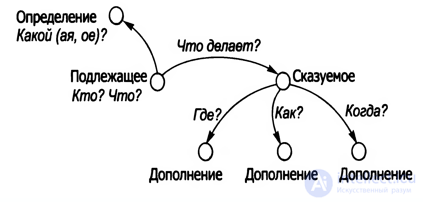
Рисунок . Пример записи алгоритма в форме графа
Стандартные графические объекты блок-схем
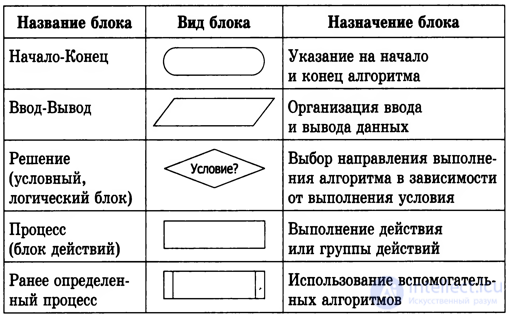
Типовые алгоритмические структуры
Хотя в определении алгоритма требуется лишь конечность числа шагов, требуемых для достижения результата, на практике выполнение огромного количество шагов приводит к длительному выполнению программ, также обычно есть другие ограничения (на размер программы, на допустимые действия). В связи с этим вводят такие понятия, как сложность алгоритма (временна́я, по размеру программы, вычислительная и другие).
Для каждой задачи может существовать множество алгоритмов, приводящих к цели. Увеличение эффективности алгоритмов составляет одну из задач информатики, начиная с 1940-х годов в связи с этим простроен ряд более эффективных в асимптотическом смысле алгоритмов для традиционных задач (например, алгоритмы быстрого умножения[en], алгоритм Чудновского для вычисления числа ).
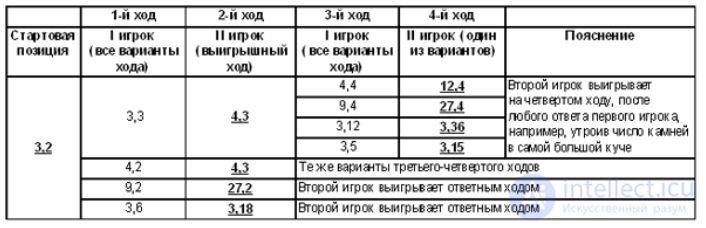
В качестве иллюстрации - как "договаривались", не вычислительной - приведем алгоритмизированное описание беседы небезызвестного почтальона Печкина с Говорящим Галчонком. Нумерация шагов в словесном описании алгоритма, соответствующей ему блок-схеме (Рис. A1-1) и диаграмме (Рис. A1-2) совпадает.
Понятие алгоритма непосредственно связано с представлением об исполнителе алгоритма
Взаимосвязь понятий отражена на рисунке:
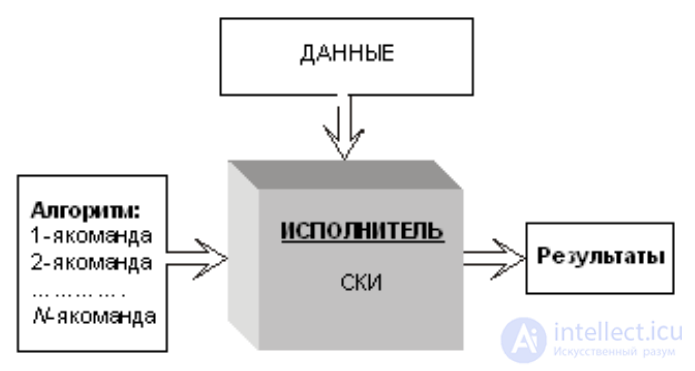

Рисунок Схема функционирования исполнителя алгоритмов
Множество команд, которые может выполнять исполнитель, составляют систему команд исполнителя (СКИ). Алгоритм строится из команд СКИ. Объекты, над которыми исполнитель может совершать действия, составляют так называемую среду исполнителя. Данные и результаты, изображенные на рисунке, — это объекты, относящиеся к среде исполнителя.
Основные свойства алгоритма (дискретность, понятность, определенность, конечность) обеспечивают возможность формальной работы исполнителя. Отсюда следует, что исполнителем алгоритмов может быть автоматическое устройство. Класс задач, на решение которых ориентирован исполнитель, определяется его системой команд.
В методике обучения алгоритмизации принято выделять две категории исполнителей: исполнители, работающие “в обстановке”, и исполнители, работающие с величинами. Для первой категории средой исполнителя может быть лист (экран), на котором исполнитель формирует изображения (рисунки, чертежи и пр.); лабиринт, который исполнитель должен преодолеть; предметы, которые исполнитель должен расставить в определенном порядке, и т.п.
Исполнители работы с величинами предназначены для обработки числовой или символьной информации. Исполнитель, в систему команд которого входят арифметические и логические операции, может решать вычислительные задачи. Входными данными и результатами для него являются числа. Универсальным исполнителем алгоритмов для работы с величинами является компьютер.
Алгоритм Евклида — эффективный метод вычисления наибольшего общего делителя (НОД). Назван в честь греческого математика Евклида; один из древнейших алгоритмов, который используют до сих пор .
Описан в «Началах» Евклида (примерно 300 лет до н. э.), а именно в книгах VII и X. В седьмой книге описан алгоритм для целых чисел, а в десятой — для длин отрезков.
Существует несколько вариантов алгоритма, ниже записанный в псевдокоде рекурсивный вариант:
Алгоритм 1.
функция нод(a, b)
если b = 0
возврат a
иначе
возврат нод(b, a mod b)



Иллюстрация выполнения алгоритма Евклида для вычисления НОД чисел 1599 и 650.
НОД чисел 1599 и 650:
| Шаг 1 | 1599 = 650*2 + 299 |
| Шаг 2 | 650 = 299*2 + 52 |
| Шаг 3 | 299 = 52*5 + 39 |
| Шаг 4 | 52 = 39*1 + 13 |
| Шаг 5 | 39 = 13*3 + 0 |
Алгоритм 1. Почтальон Печкин и Галчонок
Почтальон Печкин стучит в дверь - "тук-тук".
Если Галчонок слышит стук, то переход к шагу 3, иначе - к шагу 1. {Если птица глуховата или ее нет дома, то Печкину не позавидуешь.}
Галчонок: "Кто там?"
Если Печкин слышит вопрос "кто там?" {а если глуховат сам почтальон, то дела его опять-таки плачевны}, то переход к шагу 5, иначе - к шагу 1.
Печкин: "Это я, почтальон Печкин. Откройте дверь. Я принес письмо для вашего Мальчика".
Если Галчонок открывает дверь {надеемся, героической птице это по силам, а то вновь бедный Печкин в безвыходном положении, поскольку процесс не завершится}, то переход к шагу 7, иначе - переход к шагу 1.
Почтальон Печкин вручает конверт с письмом.
{Комментарии в скобках, здесь и выше, призваны продемонстрировать, даже на столь простом примере, как много подводных камней ждет программиста при отладке программы, если алгоритм недостаточно продуман.}
Определяющей особенностью вычислительного процесса является возможность расчленить его на отдельные, дискретные, действия, чего нельзя сказать о процессе непрерывном. В дискретном процессе Галчонок не может задать свой сакраментальный вопрос, пока постукивание продолжается. Собственно говоря, "тук-тук" и не обладает, с точки зрения алгоритма, протяженностью во времени. Это событие мгновенно, в противном случае мы бы расчленили его на k отдельных "туков", а порядковые номера шагов, начиная с третьего, увеличились бы на k-1.
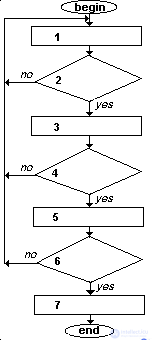
Рис. 1
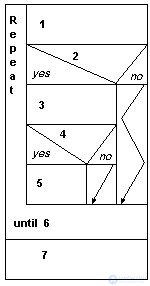
Рис. 2
Таким образом, второй особенностью является последовательность действий процесса, оформленных как предписанияалгоритма. Здесь вновь имеет место важное ограничение: так называемые параллельные алгоритмы остаются за рамками обсуждения.
Предписаний должно быть конечное число; в приведенном алгоритме их семь. Каждое из них в отдельности должно быть точными не допускать неопределенного толкования. Скажем, вопрос "кто там?" адресован вполне определенному источнику стука, располагающемуся за пределами дома около двери.
Точное предписание вызывает шаг алгоритма. Отдельные предписания могут исполняться неоднократно, поэтому ограниченность набора инструкций в алгоритме отнюдь не гарантирует обязательности его завершения. Так, если у почтальона и/или его собеседника имеются проблемы со слухом, то количество шагов алгоритма не только превысит число предписаний, но даже грозит стать бесконечным (разумеется, только теоретически: у кого-то нервы не выдержат). Поэтому обязательное требование состоит в том, что весь процесс, включающий все шаги от начала до завершения, должен быть конечен. Отметим попутно, что в теории алгоритмов рассматриваются и так называемые бесконечные алгоритмы, но они в наше поле зрения не попадут.
Вообще говоря, не столь существенно, проводится ли процесс, согласно алгоритму, именно компьютером. Содержание предписаний таково, что их может осуществить человек, а иногда даже, как видим, почти обыкновенные галки. Разница, если иметь ввиду собственно достижение результата, только в требуемом для исполнения алгоритма времени. Следовательно, нужно отличать теоретическую "мгновенность" шага алгоритма от реального времени осуществления его вычислительным устройством. И даже компьютеру может оказаться не по силам алгоритм, состоящий из конечного, но столь большого числа шагов, что окончания работы "заказчику" практически не дождаться.
Естественно, процесс должен преследовать конкретную цель, без чего постановка задачи с алгоритмическим содержанием смысла не имеет. Так, бесцельный процесс "переливания из пустого в порожнее" отнести к разряду алгоритмических мы не рискнем.
Кроме того, цель должна быть достижимой. Глухой Печкин, как мы уже выяснили, вынужден стучать в дверь бесконечно, так и не вручив письмо. К счастью, имея дело с кругом задач дискретной математики, беспокоиться не о чем, поскольку для них собственно факт существования решения, то есть алгоритма достижения поставленной цели, - редко подвергается сомнению.
Однако провести анализ алгоритма разработчику следует, чтобы оценить, сколь велико оказывается число шагов. Мораль ордена иезуитов - "цель оправдывает средства" - здесь не действует.
Как пишет Кнут, "программист может многому научиться, прочитав хорошую поваренную книгу". Вероятно, он имел ввиду, что такое чтение стало бы неплохой тренировкой в поиске ошибок и неточностей, связанных, в том числе, с разницей в бытовом и "компьютерном" представлениях об алгоритме. Что ж, проведем, следуя рекомендации, небольшую тренировку.
Беру с полки одну из подходящих случаю книг - попались "Мясные и грибные блюда" (1984). Открываю наугад: стр.45. Рецепт, если вы не являетесь вегетарианцем, выглядит заманчиво: "жаркое из говядины (ростбиф)". Нетрудно догадаться, что на выходекулинарного процесса ожидается готовый к употреблению ростбиф, что и составляет сформулированную в названии рецепта цель.
Представить алгоритм без выходных данных затруднительно: зачем он тогда нужен? И все же рискнем. Вспомним миф о Сизифе: целью процесса было не закатывание камня на вершину горы, а наказание нечестивца. Прояви Зевс чуть больше гуманности, и пожизненное наказание можно было бы заменить фиксированным числом шагов алгоритма. При необходимости задержкиосновного вычислительного процесса можно добавить внутрь него как отдельный шаг вызов процедуры, которая выполняет заданное число каких-нибудь операций с невостребованным итогом. Этот подпроцесс не формирует выходных данных. Впрочем, вы можете и не согласиться с предлагаемой трактовкой, интерпретируя как выходное значение сам факт завершения подпроцесса, поскольку в том и состояла цель его запуска.
Что же касается входной информации, то она действительно требуется не всякому алгоритму. В нашем рецепте входные данныеприсутствуют - это перечисленные ингредиенты: 1 кг говядины (филе или спинная часть), 50 г жира, соль, перец, 30 г сливочного масла, хрен, вода. В сумке Печкина их тоже можно отыскать (не продукты, а входные данные!) - это письмо, которое почтальон собирается вручить адресату. А вот в задании "нарисовать квадрат произвольного размера, пользуясь циркулем и линейкой" оговорен лишь конечный результат, а на входе - ничего.
Кроме входных и выходных данных, как правило, алгоритм предусматривает временное формирование промежуточных данных, которые вновь поступят на обработку. Исходные 50 г жира, когда повар растопит их на сковороде, переходят, согласно законам физики и кулинарии, в промежуточное состояние.
В том же рецепте примерно на полстраницы приводится описание технологического процесса, цитировать которое здесь не станем из опасения, что читатель забудет, исходя слюной, основной предмет обсуждения. Остановимся только на некоторыхнеточных инструкциях, которые несут неполную информацию. Вот одна из них: "филе жарят 20-25 минут". Так 20 или 25? Без должного поварского опыта, который никак не отражен в описании, остается определенный риск завершить "алгоритмическую обработку" несъедобным результатом.
Чтобы исключить подобный исход вычислительного процесса, нужно при конструировании алгоритма строго определить каждый его шаг, предусмотрев любые возможные состояния процесса и соответствующие инструкции для их обработки. Только такой алгоритм гарантирует однозначное получение требуемого результата и классифицируется как детерминированный. Относительно такого алгоритма можно утверждать, что его неоднократное применение к одинаковым входным данным всегда приводит к одному итогу.
В противоположность детерминированному, в алгоритме стохастическом заложена некоторая неопределенность в выборе очередной инструкции. Таков был случайный выбор рецепта жаркого: при повторении манипуляции с поваренной книгой я, скорее всего, открою ее на другой странице. Но это не значит, что вычислительному устройству угрожает положение буриданова осла и оно может перейти в состояние летаргической паузы. Напротив, выбор конкретной инструкции непременно происходит, только - на основе вероятностного механизма. При этом разработчик алгоритма планирует, что, независимо от выбранного продолжения, конечный результат будет удовлетворять условиям поставленной задачи. Так, нашему мясному полуфабрикату не повредят ни 20 минут прожаривания, ни 25 минут, ни любое промежуточное значение, и в итоге заказчик получит именно ростбиф.
Нередко, перечисляя непременные свойства алгоритма, к их числу относят "массовость", имея ввиду возможность его применения "для решения однотипных задач". Универсальность этого требования вызывает сомнения, поскольку "штучное" предназначение некоторых алгоритмов представляется достаточно разумным. Например, рассказав друзьям анекдот, станете ли вы пересказывать его в той же аудитории? Удастся ли вам в другой компании повторить процесс без малейших отклонений? А как здесь иначе интерпретировать "однотипность", я не знаю.
Если говорить только о вычислительных процедурах, то предлагаю в качестве контрпримера компьютерную программу, существующую в единственном экземпляре на жестком диске. Будучи запущенной, она форматирует винчестер, а стало быть, стирает и себя, что делает повторное исполнение алгоритма невозможным.
Наконец, читателям-скептикам, которые сомневаются в правомерности последних примеров для опровержения свойства "массовости", предлагаю выполнить алгоритмическое
Упражнение 1
Как известно из замечательной книги Л.Лагина, однажды со Стариком Хоттабычем приключился неприятный инцидент: он съел много эскимо, отчего сильно простыл. Предположим, для упрощения, что за 5 минут выполняется 1 шаг алгоритма: съедается очередная порция (в действительности, старик справился со всем запасом мороженого за пять минут). Подсчитайте (процесс - вычислительный!), сколько вам понадобится алгоритмических шагов для достижения того же результата (Хоттабычу "хватило" 43 порций). Если найдется хотя бы пара читателей, повторивших или превзошедших славное достижение Хоттабыча, то автор готов признать за указанным алгоритмом свойство массовости.
А как ты думаешь, при улучшении алгоритм, будет лучше нам? Надеюсь, что теперь ты понял что такое алгоритм, исполнители алгоритмов, блок-схема, виды алгоритмов , анализ алгоритмов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Часть 1 Алгоритм: понятие, терминология, свойства, запись
Часть 2 Нумерация алгоритмов - Алгоритм: понятие, терминология, свойства, запись
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов