Лекция
Привет, сегодня поговорим про сортировка шелла, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое сортировка шелла , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
В 1959 году американский ученый Дональд Шелл опубликовал алгоритм сортировки, который впоследствии получил его имя – « сортировка шелла ». Этот алгоритм может рассматриваться и как обобщение пузырьковой сортировки, так и сортировки вставками.
Сортировка Шелла (англ. Shell sort) — алгоритм сортировки, являющийся усовершенствованным вариантом сортировки вставками. Идея метода Шелла состоит в сравнении элементов, стоящих не только рядом, но и на определенном расстоянии друг от друга. Иными словами — это сортировка вставками с предварительными «грубыми» проходами. Аналогичный метод усовершенствования пузырьковой сортировки называется сортировка расческой.
Идея метода заключается в сравнение разделенных на группы элементов последовательности, находящихся друг от друга на некотором расстоянии. Изначально это расстояние равно d или N/2, где N — общее число элементов. На первом шаге каждая группа включает в себя два элемента расположенных друг от друга на расстоянии N/2; они сравниваются между собой, и, в случае необходимости, меняются местами. На последующих шагах также происходят проверка и обмен, но расстояние d сокращается на d/2, и количество групп, соответственно, уменьшается. Постепенно расстояние между элементами уменьшается, и на d=1 проход по массиву происходит в последний раз.
Далее, на примере последовательности целых чисел, показан процесс сортировки массива методом Шелла. Для удобства и наглядности, элементы одной группы выделены одинаковым цветом.
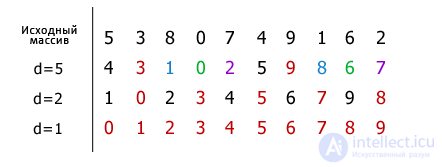
Первое значение, соответствующее расстоянию d равно 10/2=5. На каждом шаге оно уменьшается вдвое. Элементы, входящие в одну группу, сравниваются и если значение какого-либо элемента, стоящего левее того с которым он сравнивается, оказывается больше (сортировка по возрастанию), тогда они меняются местами. Так, элементы путем внутригрупповых перестановок постепенно становятся на свои позиции, и на последнем шаге (d=1) сортировка сводится к проходу по одной группе, включающей в себя все N элементов массива. При этом число требуемых обменов оказывается совсем небольшим.
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
#include "stdafx.h"
#include using namespace std; int i, j, n, d, count; void Shell(int A[], int n) //сортировка Шелла { d=n; d=d/2; while (d>0) { for (i=0; i{ j=i; while (j>=0 && A[j]>A[j+d]) { count=A[j]; A[j]=A[j+d]; A[j+d]=count; j--; } } d=d/2; } for (i=0; i} //главная функция void main() { setlocale(LC_ALL,"Rus"); cout<<"Размер массива > "; cin>>n; int *A= new int[n]; //объявление динамического массива for (i=0; i{ cout< "; cin>>A[i]; } cout<<"\nРезультирующий массив: "; Shell(A, n); delete [] A; //освобождение памяти system("pause>>void"); } |
|
1
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
program ShellSorting;
uses crt; type massiv=array[1..100] of integer; var i, j, n, d, count: integer; A: massiv; procedure Shell(A: massiv; n: integer); {сортировка Шелла} begin d:=n; d:=d div 2; while (d>0) do begin for i:=1 to n-d do begin j:=i; while ((j>0) and (A[j]>A[j+d])) do begin count:=A[j]; A[j]:=A[j+d]; A[j+d]:=count; j:=j-1; end; end; d:=d div 2; end; writeln; for i:=1 to n do write(' ', A[i]); {вывод массива} end; {основной блок программы} begin write('Размер массива > '); read(n); for i:=1 to n do {ввод массива} begin write(i, ' элемент > '); readln(A[i]); end; write('Результирующий массив: '); Shell(A, n); end. |
template< typename RandomAccessIterator, typename Compare >
void shell_sort( RandomAccessIterator first, RandomAccessIterator last, Compare comp )
{
for( auto d = ( last - first ) / 2; d != 0; d /= 2 )
//нужен цикл для first = a[0..d-1]
for( auto i = first + d; i != last; ++i )
for( auto j = i; j - first >= d && comp( *j, *( j - d ) ); j -= d )
std::swap( *j, *( j - d ) );
}
void ShellSort (int array[], int size) // * ∆k = (b∆k−1)/2 ∆0 = N
{
int step, i, j, tmp;
// Выбор шага
for (step = size / 2; step > 0; step /= 2)
// Перечисление элементов, которые сортируются на определенном шаге
for (i = step; i < size; i++)
// Перестановка элементов внутри подсписка, пока i-тый не будет отсортирован
for (j = i - step; j >= 0 && array[j] > array[j + step]; j -= step)
{
tmp = array[j];
array[j] = array[j + step];
array[j + step] = tmp;
}
}
for (int step = n / 2; step > 0; step /= 2) {
for (int i = step; i < n; i++) {
for (int j = i - step; j >= 0 && a[j] > a[j + step] ; j -= step) {
int x = a[j];
a[j] = a[j + step];
a[j + step] = x;
}
}
}
def shell_sort(data: List[int]) -> List[int]:
last_index = len(data) - 1
step = len(data)//2
while step > 0:
for i in range(last_index):
j = i + step
if j > last_index:
break
if data[i] > data[j]:
data[i], data[j] = data[j], data[i]
step //= 2
return data
Сортировка Шелла уступает в эффективности быстрой сортировки, но выигрывает у сортировки вставками. Об этом говорит сайт https://intellect.icu . Сравнить скорость работы этих трех алгоритмов можно, воспользовавшись следующей таблицей.
|
Сортировка вставками |
Сортировка Шелла |
Быстрая сортировка |
|
|
Худший случай |
O(n2) |
O(n2) |
O(n2) |
|
Лучший случай |
O(n) |
O(n log n) |
O(n log n) |
|
Средний случай |
O(n2) |
Зависит от расстояния между элементами |
O(n log n) |
|
Алгоритмы сортировки
|
|
|---|---|
| Теория |
Сложность О-нотация Отношение порядка Типы сортировки Устойчивая Внутренняя Внешняя |
| Обменные |
Сортировка пузырьком , Сортировка перемешиванием , Сортировка гномья, Сортировка быстрая, Сортировка расческой , Сортировка чет-нечет , Сортировка поразрядная |
| Выбором |
Сортировка выбором , Сортировка пирамидальная, Сортировка плавная |
| Вставками |
Сортировка вставками , Сортировка Шелла , Сортировка деревом |
| Слиянием |
Сортировка cлиянием |
| Без сравнений |
Сортировка подсчетом , Сортировка блочная |
| Гибридные |
Сортировка Introsort, Сортировка Timsort |
| Прочее |
Сортировка Топологическая , Сортировка сети, Сортировка Битонная |
| Непрактичные |
Сортировка Bogosort, Сортировка Stooge sort , Сортировка Блинная, медленная сортировка |
На этом все! Теперь вы знаете все про сортировка шелла, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое сортировка шелла и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Из статьи мы узнали кратко, но содержательно про сортировка шелла
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов