Стены (решение через графы)

Привет, сегодня поговорим про стены решение через графы , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое стены решение через графы , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

Международная олимпиада по информатике, 2000

Задание

В некоторой стране стены построены таким образом, что каждая стена соединяет ровно два города, и стены не пересекают друг друга. Таким образом, страна разделена на отдельные части. Чтобы добраться из одной области в другую, необходимо либо пройти через город, либо пересечь стену. Два любых города А и В могут соединяться не более чем одной стеной (один конец стены в городе A, другой — в городе В). Более того, всегда существует путь из города А в город В, проходящий вдоль каких-либо стен и через города.

 
Существует клуб, члены которого живут в городах. В каждом городе может жить либо один член клуба, либо вообще ни одного. Иногда у членов клуба возникает желание встретиться внутри одной из областей, но не в городе. Чтобы попасть в нужную область, каждый член клуба должен пересечь какое-то множество стен, возможно, равное нулю. Члены клуба путешествуют на велосипедах. Они не хотят въезжать ни в один город из-за интенсивного движения на городских улицах. Они также хотят пересечь минимально возможное количество стен, так как пересекать стену с велосипедом довольно трудно. Исходя из этого, нужно найти такую оптимальную область, чтобы суммарное количество стен, которые требуется пересечь членам клуба, называемое суммой пересечений, было минимальным из всех возможных.

 
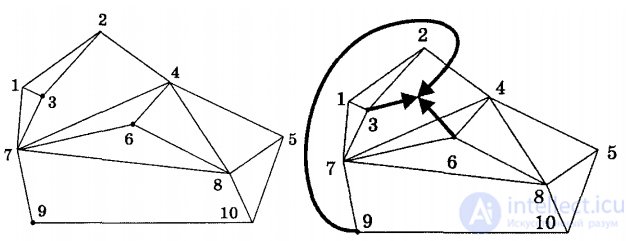
Города пронумерованы целыми числами от 1 до N, где N — количество городов. На рисунке справа (выше) пронумерованные вершины обозначают города, а линии, соединяющие вершины, обозначают стены. Предположим, членами клуба являются три человека, которые живут в городах с номерами 3,6 и 9. Тогда оптимальная область и соответствующие маршруты движения членов клуба показаны на рисунке ниже. Сумма пересечений равна 2, так как членам клуба требуется пересечь две стены: человеку из города 9 требуется пересечь стену между городами 2 и 4, человеку из города 6 требуется пересечь стену между городами 4 и 7, а человек из города 3 не пересекает стен вообще.

Требуется написать программу, которая по заданной информации о городах, областях и местах проживания членов клуба находит оптимальную область и минимальную сумму пересечений.

Ввод

Первая строка содержит одно целое число: количество областей M, удовлетворяющее неравенствам 2 <= М <= 200. Об этом говорит сайт https://intellect.icu . Вторая строка содержит одно целое число: количество городов N, причем 3 <= N <= 250. Третья строка содержит одно целое число: количество членов клуба L, причем 1 <= L <= 30 и L <= N.

Четвертая строка содержит L различных целых чисел в возрастающем порядке: номера городов, где живут члены клуба.

Оставшаяся часть файла содержит 2М строк, по паре строк для каждой из M областей. Первые две строки описывают первую область, вторые две строки — вторую область, и т. д. В каждой паре первая строка содержит количество городов на границе области; вторая содержит номера этих I городов в порядке обхода границы области по часовой стрелке. Единственным исключением является последняя область — это находящаяся снаружи (внешняя) область, окружающая все города и другие области, и для нее порядок следования городов на границе задается против часовой стрелки.

Порядок описания областей во входном файле задает целые номера этим областям. Область, описанная первой во входном файле, имеет номер 1, описанная второй — номер 2, и т. д. Обратите внимание, что входной файл содержит описание всех областей, образованных городами и стенами, включая находящуюся снаружи (внешнюю) область.

Вывод

Первая строка этого файла содержит одно целое число — минимальную сумму пересечений. Вторая строка содержит одно целое число — номер оптимальной области. Если существует несколько различных решений, вам необходимо найти лишь одно из них.

Пример ввода         Пример вывода
10                   2
10                   3
3 
3 6 9 
3 
1 2 3 
3 
1 3 7 
4 
2 4 7 3 
3 
4 6 7 
3 
4 8 6 
3 
6 8 7 
3 
4 5 8 
4 
7 8 10 9 
3 
5 10 8 
7 
7 9 10 5 4 2 1 

Решение      

Основная идея заключается в том, чтобы преобразовать данную задачу к задаче на графе следующим образом: пусть вершины — это области, образованные стенами. Наличие ребра означает смежность областей. Для перехода в смежную область требуется перелезть ровно одну стену. Например, для данных из примера ввода получим граф из 10 вершин (10 областей), связанных ребрами (смежные области) следующим образом:

Область  Смежные области 
1        2 3 10 
2        1 3 10 
3        1 2 4 10 
4        3 5 6 10 
5        4 6 7 
6        4 5 8 
7        5 9 10 
8        6 9 10 
9        7 8 10 
10       1 2 3 4 7 8 9  

Нужно найти такую вершину на графе, чтобы сумма расстояний к ней из городов, где живут члены клуба, была минимальной. Каждый город может быть граничным для нескольких областей. Поэтому для каждого города нужно выбирать наиболее выгодную область, среди его граничных областей.

Для установления факта смежности областей используется следующий алгоритм. Если списки городов, ограничивающих области (t[i] и t[j]), включают 2 одинаковых города, значит, эти области являются смежными, поскольку они имеют общую стену, соединяющую эти два города.

Для реализации установки факта наличия двух общих чисел используются два массива, которые содержат 1 на позициях городов, ограничивающих область, и 0 на всех остальных позициях. Если единицы встречаются в обоих областях на одних и тех же позициях более двух раз, то области смежные.

С помощью алгорима Флойда находим кратчайшие расстояния G[i,j] на построенном графе между всеми парами вершин (i,j).

Далее циклом по всем областям находим минимальную стоимость проведения сбора членов клуба именно в ней и среди этих значений находим минимальное и номер соответствующей области. Для каждого члена клуба в качестве области, из которой он отправится в путь, нужно последовательно выбирать все области, смежные с городом, запоминая ту, которая имеет кратчайший путь к текущему месту сбора.

Формальное описание     

Walls()
1. Прочитать из файла информацию про области, принять области вершинами 
   графа.
2. Пока не обработаны все пары областей, повторять пп.2.1-2.4:
   2.1. Инициализировать количество общих городов нулем.
   2.2. Перебрать все города. Если город принадлежит обоим областям, то
        увеличить количество общих городов на 1.
   2.3. Если существует больше одного общего города для текущей пары
        областей, то связать вершины-области ребром.
   2.4. Перейти к следующей паре областей.
3. Использовать алгоритм Флойда-Уоршелла для нахождения расстояний между 
   всеми парами областей (выполнить пп. 3.1-3.2):
   3.1. Инициализировать расстояний бесконечностью.
   3.2. Для каждой тройки областей, повторять пп. 3.2.1-3.2.2:
        3.2.1. Если длина пути из первой области во вторую через третью 
               меньше, чем из первой во вторую, то считать, что путь через
               третью вершину минимальным.
        3.2.2. Перейти к следующей тройке областей.
4. Выбрать первую область.
5. Пока не просмотрены все области, повторять пп. 5.1-5.3:
   5.1. Найти сумму расстояний от областей, где живут члены клуба до 
        текущей области, при этом выбирать оптимальную область для 
        членов клуба.
   5.2. Если сумма до текущей вершины меньше чем минимальная, то считать 
        данную сумму минимальной, а текущую область - оптимальной.
   5.3. Перейти к следующей области. 
6. Вывести номер оптимальной области и сумму расстояний до нее.

На этом все! Теперь вы знаете все про стены решение через графы , Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое стены решение через графы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов