Лекция
Привет, Вы узнаете о том , что такое рекурсия, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое рекурсия, анализ сложности рекурсивных алгоритмов, анализ рекурсивных алгоритмов , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
рекурсия — это свойство объекта подражать самому себе. Объект является рекурсивным если его части выглядят также как весь объект. Рекурсия очень широко применяется в математике и программировании:
Статья посвящена анализу трудоемкости рекурсивных алгоритмов, приведены необходимые математические сведения, рассмотрены примеры. Кроме того, описана возможность замены рекурсии циклом, хвостовая рекурсия.
Рекурсивный алгоритм всегда разбивает задачу на части, которые по своей структуре являются такими же как исходная задача, но более простыми. Для решения подзадач функция вызывается рекурсивно, а их результаты каким-либо образом объединяются. Разделение задачи происходит лишь тогда, когда ее не удается решить сразу (она является слишком сложной).
Например, задачу обработки массива нередко можно свести к обработке его частей. Деление на части выполняется до тех пор, пока они не станут элементарными, т.е. достаточно простыми чтобы получить результат без дальнейшего упрощения.
Алгоритм делит исходный массив на две части — первый элемент и массив из остальных элементов. Выделяется два простых случая, когда разделение не требуется — обработаны все элементы или первый элемент является искомым.
В алгоритме поиска разделять массив можно было бы и иначе (например пополам), но это не сказалось бы на эффективности. Если массив отсортирован — то его деление пополам целесообразно, т.к. на каждом шаге количество обрабатываемых данных можно сократить на половину.
Двоичный поиск выполняется над отсортированным массивом. На каждом шаге искомый элемент сравнивается со значением, находящимся посередине массива. В зависимости от результатов сравнения либо левая, либо правая части могут быть «отброшены».
Числа Фибоначчи определяются рекуррентным выражением, т.е. таким, что вычисление элемента которого выражается из предыдущих элементов: F0=0,F1=1,Fn=Fn−1+Fn−2,n>2.
Алгоритм быстрой сортировки на каждом шаге выбирает один из элементов (опорный) и относительно него разделяет массив на две части, которые обрабатываются рекурсивно. Об этом говорит сайт https://intellect.icu . В одну часть помещаются элементы меньше опорного, а в другую — остальные.
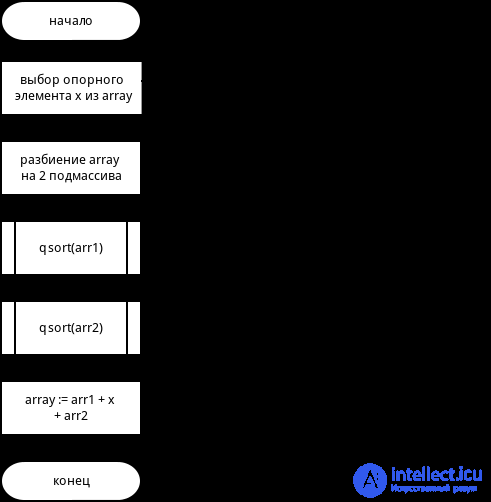
Блок-схема алгоритма быстрой сортировки
В основе алгоритма сортировки слиянием лежит возможность быстрого объединения упорядоченных массивов (или списков) так, чтобы результат оказался упорядоченным. Алгоритм разделяет исходный массив на две части произвольным образом (обычно пополам), рекурсивно сортирует их и объединяет результат. Разделение происходит до тех пор, пока размер массива больше единицы, т.к. пустой массив и массив из одного элемента всегда отсортированы.
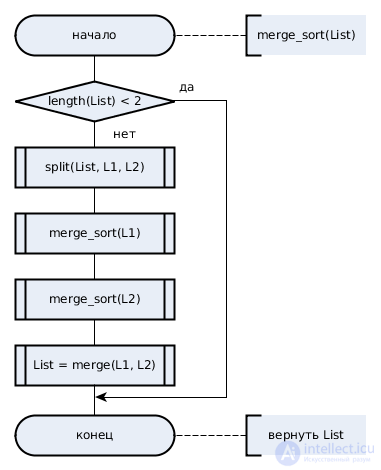
Блок схема сортировки слиянием
На каждом шаге слияния из обоих списков выбирается первый необработанный элемент. Элементы сравниваются, наименьший из них добавляется к результату и помечается как обработанный. Слияние происходит до тех пор, пока один из списков не окажется пуст.
При анализе сложности циклических алгоритмов рассчитывается трудоемкость итераций и их количество в наихудшем, наилучшем и среднем случаях . Однако не получится применить такой подход к рекурсивной функции, т.к. в результате будет получено рекуррентное соотношение. Например, для функции поиска элемента в массиве:
Рекуррентные отношения не позволяют нам оценить сложность — мы не можем их просто так сравнивать, а значит, и сравнивать эффективность соответствующих алгоритмов. Необходимо получить формулу, которая опишет рекуррентное отношение — универсальным способом сделать это является подбор формулы при помощи метода подстановки, а затем доказательство соответствия формулы отношению методом математической индукции.
Заключается в последовательной замене рекуррентной части в выражении для получения новых выражений. Замена производится до тех пор, пока не получится уловить общий принцип и выразить его в виде нерекуррентной формулы. Например для поиска элемента в массиве:
Мы вывели формулу, однако первый шаг содержит предположение, т.е. не имеется доказательства соответствия формулы рекуррентному выражению — получить доказательство позволяет метод математической индукции.
Позволяет доказать истинность некоторого утверждения (Pn), состоит из двух шагов:
Докажем корректность предположения, сделанного при оценки трудоемкости функции поиска
( 
=(n+1)×O(1)):
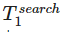=2×O(1) верно из условия (можно подставить в исходную рекуррентную формулу);
=(n+1)×O(1);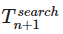
=((n+1)+1)×O(1)=(n+2)×O(1);
=O(1)+(n+1)×O(1)=(n+2)×O(1);
утверждение доказано.
Часто, такое доказательство — достаточно трудоемкий процесс, но еще сложнее выявить закономерность используя метод подстановки. В связи с этим применяется, так называемый, общий метод .
Общий метод не является универсальным, например с его помощью невозможно провести оценку сложности приведенного выше алгоритма вычисления чисел Фибоначчи. Однако, он применим для всех случаев использования подхода «разделяй и властвуй» :
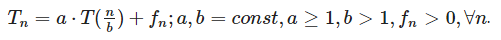
Уравнения такого вида получаются если исходная задача разделяется на a подзадач, каждая из которых обрабатывает nb элементов. fn — трудоемкость операций разбиения задачи на части и комбинирование решений. Помимо вида соотношения, общий метод накладывает ограничения на функцию fn, выделяя три случая:
Правильность утверждений для каждого случая доказана формально . Задача анализа рекурсивного алгоритма теперь сводится к определению случая основной теоремы, которому соответствует рекуррентное соотношение.
Алгоритм разбивает исходные данные на 2 части (b = 2), но обрабатывает лишь одну из них (a = 1), 
. Функция разделения задачи и компоновки результата растет с той же скоростью, что и 
значит необходимо использовать второй случай теоремы:
Рекурсивная функция разбивает исходную задачу на одну подзадачу (a = 1), данные делятся на одну часть (b = 1). Мы не можем использовать основную теорему для анализа этого алгоритма, т.к. не выполняется условие b>1.
Для проведения анализа может использоваться метод подстановки или следующие рассуждения: каждый рекурсивный вызов уменьшает размерность входных данных на единицу, значит всего их будет n штук, каждый из которых имеет сложность
O(1). Тогда
Исходные данные разделяются на две части, обе из которых обрабатываются: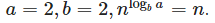 
При обработке списка, разделение может потребовать выполнения Θ(n) операций, а для массива — выполняется за постоянное время (Θ(1)). Однако, на соединение результатов в любом случае будет затрачено Θ(n), поэтому fn=n.
Используется второй случай теоремы: 
В лучшем случае исходный массив разделяется на две части, каждая из которых содержит половину исходных данных. Разделение потребует выполнения n операций. Трудоемкость компоновки результата зависит от используемых структур данных — для массива O(n), для связного списка O(1). a=2,b=2,fn=b, значит сложность алгоритма будет такой же как у сортировки слиянием: TquickSortn=O(n⋅logn).
Однако, в худшем случае в качестве опорного будет постоянно выбираться минимальный или максимальный элемент массива. Тогда b=1, а значит, мы опять не можем использовать основную теорему. Однако, мы знаем, что в этом случае будет выполнено n рекурсивных вызовов, каждый из которых выполняет разделение массива на части (O(n)) — значит сложность алгоритма TquickSortn=O(n2).
При анализе быстрой сортировки методом подстановки, пришлось бы также рассматривать отдельно наилучший и наихудший случаи.
Анализ трудоемкости рекурсивных функций значительно сложнее аналогичной оценки циклов, но основной причиной, по которой циклы предпочтительнее являются высокие затраты на вызов функции.
После вызова управление передается другой функции. Для передачи управления достаточно изменить значение регистра программного счетчика, в котором процессор хранит номер текущей выполняемой команды — аналогичным образом передается управление ветвям алгоритма, например, при использовании условного оператора. Однако, вызов — это не только передача управления, ведь после того, как вызванная функция завершит вычисления, она должна вернуть управление в точку, и которой осуществлялся вызов, а также восстановить значения локальных переменных, которые существовали там до вызова.
Для реализации такого поведения используется стек (стек вызовов, call stack) — в него помещаются номер команды для возврата и информация о локальных переменных. Стек не является бесконечным, поэтому рекурсивные алгоритмы могут приводить к его переполнению, в любом случае на работу с ним может уходить значительная часть времени.
В ряде случаев рекурсивную функцию достаточно легко заменить циклом, например, рассмотренные выше алгоритмы поиска и бинарного поиска . В некоторых случаях требуется более творческий подход, но чаще всего такая замена оказывается возможной. Кроме того, существует особый вид рекурсии, когда рекурсивный вызов является последней операцией, выполняемой функцией. Очевидно, что в таком случае вызывающая функция не будет каким-либо образом изменять результат, а значит ей нет смысла возвращать управление. Такая рекурсия называется хвостовой — компиляторы автоматически заменяют ее циклом.
Зачастую сделать рекурсию хвостовой помогает метод накапливающего параметра , который заключается в добавлении функции дополнительного аргумента-аккумулятора, в котором накапливается результат. Функция выполняет вычисления с аккумулятором до рекурсивного вызова. Хорошим примером использования такой техники служит функция вычисления факториала:
В качестве более сложного примера рассмотрим функцию вычисления чисел Фибоначчи. Основная функция вызывает вспомогательную,использующую метод накапливающего параметра, при этом передает в качестве аргументов начальное значение итератора и два аккумулятора (два предыдущих числа Фибоначчи).
Функция с накапливающим параметром возвращает накопленный результат, если рассчитано заданное количество чисел, в противном случае — увеличивает счетчик, рассчитывает новое число Фибоначчи и производит рекурсивный вызов. Оптимизирующие компиляторы могут обнаружить, что результат вызова функции без изменений передается на выход функции и заменить его циклом. Такой прием особенно актуален в функциональных и логических языках программирования, т.к. в них программист не может явно использовать циклические конструкции.
Исследование, описанное в статье про рекурсия, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое рекурсия, анализ сложности рекурсивных алгоритмов, анализ рекурсивных алгоритмов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов