Лекция
Привет, Вы узнаете о том , что такое интерполяционный поиск, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое интерполяционный поиск, интерполирующий поиск , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
Интерполяционный поиск ( интерполирующий поиск ) основан на принципе поиска в телефонной книге или, например, в словаре. Вместо сравнения каждого элемента с искомым, как при линейном поиске, данный алгоритм производит предсказание местонахождения элемента: поиск происходит подобно двоичному поиску, но вместо деления области поиска на две части, интерполирующий поиск производит оценку новой области поиска по расстоянию между ключом и текущим значением элемента. Другими словами, бинарный поиск учитывает лишь знак разности между ключом и текущим значением, а интерполирующий еще учитывает и модуль этой разности и по данному значению производит предсказание позиции следующего элемента для проверки. В среднем интерполирующий поиск производит log(log(N)) операций, где N есть число элементов, среди которых производится поиск. Число необходимых операций зависит от равномерности распределения значений среди элементов. В плохом случае (например, когда значения элементов экспоненциально возрастают) интерполяционный поиск может потребовать до O(N) операций.
Интерполяция может производиться на основе функции, аппроксимирующей распределение значений, либо набора кривых, выполняющих аппроксимацию на отдельных участках. В этом случае поиск может завершиться за несколько проверок. Преимущества этого метода состоят в уменьшении запросов на чтение медленной памяти (такой, как, например, жесткий диск), если запросы происходят часто. Такой подход становится похожим на частный случай поиска с использованием хеш-таблицы.
Часто анализ и построение аппроксимирующих кривых не требуется, показательный случай здесь — когда все элементы отсортированы по возрастанию. В таком списке минимальное значение будет по индексу 1, а максимальное по индексу N. В этом случае аппроксимирующую кривую можно принять за прямую и применять линейную интерполяцию.
Рассмотрим задачу: найти слово в словаре. Если оно начинается на букву "Б", то никто не будет искать его в середине, а откроет словарь ближе к началу. В чем разница между алгоритмом человека и другими? Отличие заключается в том, что алгоритмы вроде двоичного поиска не делают различий между "немного больше" и "существенно больше".
В основе интерполяционного поиска лежит операция интерполирование. Интерполирование – нахождение промежуточных значений величины по имеющемуся дискретному набору известных значений. интерполяционный поиск работает только с упорядоченными массивами; он похож на бинарный, в том смысле, что на каждом шаге вычисляется некоторая область поиска, которая, по мере выполнения алгоритма, сужается. Об этом говорит сайт https://intellect.icu . Но в отличие от двоичного, интерполяционный поиск не делит последовательность на две равные части, а вычисляет приблизительное расположение ключа (искомого элемента), ориентируясь на расстояние между искомым и текущим значением элемента. Идея алгоритма напоминает хорошо знакомый старшим поколениям поиск телефонного номера в обычном справочнике: список имен пользователей упорядочен, поэтому не составит труда найти нужного пользователя, так как, если мы, например, ищем пользователя с логином , начинающимся на букву «Э», то для дальнейшего поиска разумно будет перейти в конеце списка.
Формула, определяющая алгоритм интерполяционного поиска выглядит следующим образом:
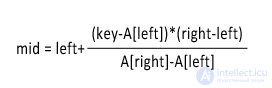
Здесь mid – номер элемента, с которым сравнивается значение ключа, key – ключ (искомый элемент), A – массив упорядоченных элементов, left и right – номера крайних элементов области поиска . Важно отметить, операция деления в формуле строго целочисленная, т. е. дробная часть, какая бы она ни была, отбрасывается.
Пусть a — отсортированный массив из nn чисел, xx — значение, которое нужно найти. Поиск происходит подобно двоичному поиску, но вместо деления области поиска на две примерно равные части, интерполирующий поиск производит оценку новой области поиска по расстоянию между ключом и текущим значением элемента. Если известно, что x лежит между al и ar , то следующая проверка выполняется примерно на расстоянии
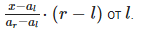
Формула для разделительного элемента m получается из следующего уравнения:
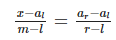
— откуда следует, что
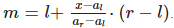
На рисунке внизу показано, из каких соображений берется такая оценка. Интерполяционный поиск основывается на том, что наш массив представляет из себя что-то наподобии арифметической прогрессии.
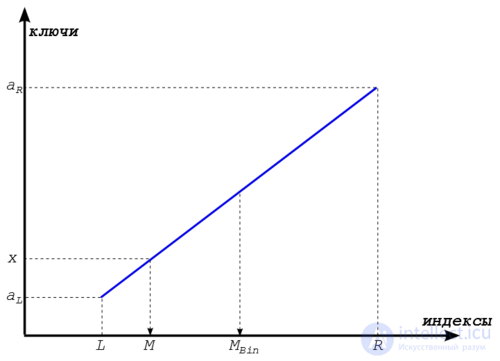
Асимптотически интерполяционный поиск превосходит по своим характеристикам бинарный. Если ключи распределены случайным образом, то за один шаг алгоритм уменьшает количество проверяемых элементов с n до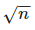 
. То есть, после k -ого шага количество проверяемых элементов уменьшается до 
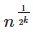. Значит, остается проверить только 2 элемента (и закончить на этом поиск), когда 
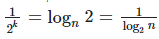. Из этого вытекает, что количество шагов, а значит, и время работы составляет 
.
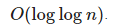При "плохих" исходных данных (например, при экспоненциальном возрастании элементов) время работы может ухудшиться до O(n).
Эксперименты показали, что интерполяционный поиск не настолько снижает количество выполняемых сравнений, чтобы компенсировать требуемое для дополнительных вычислений время (пока таблица не очень велика). Кроме того, типичные таблицы недостаточно случайны, да и разница между значениями log(log(n)) и log(n) становится значительной только при очень больших n . На практике при поиске в больших файлах оказывается выгодным на ранних стадиях применять интерполяционный поиск, а затем, когда диапазон существенно уменьшится, переходить к двоичному.
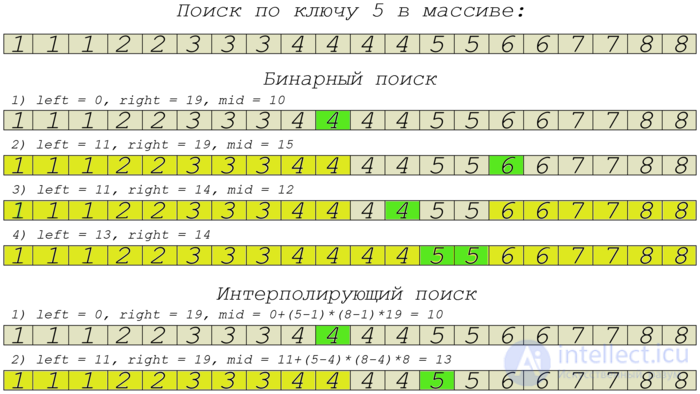
Следующий пример на Java показывает простейшую реализацию интерполирующего поиска. На каждой стадии алгоритм рассчитывает позицию для следующей проверки, как при двоичном поиске, переносит верхнюю или нижнюю границу, определяя тем самым новую область поиска, содержащую искомое значение.
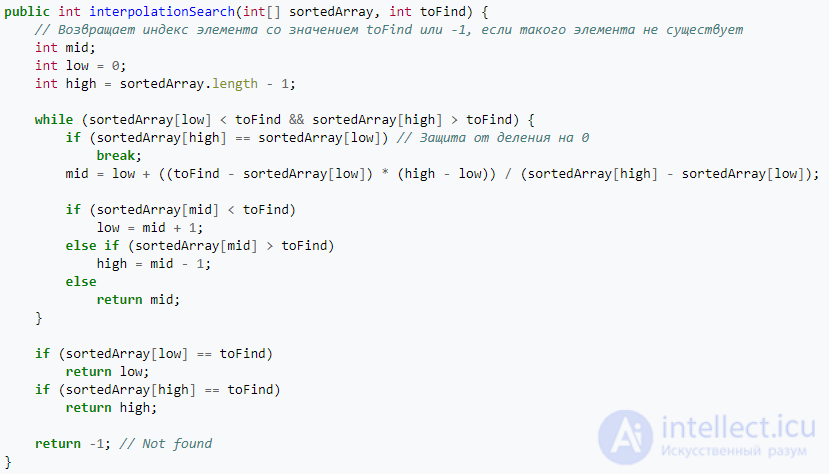
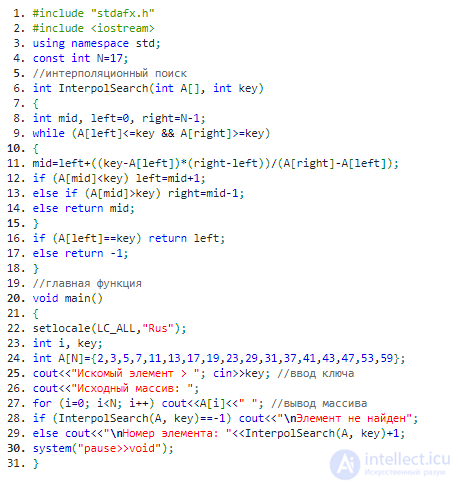
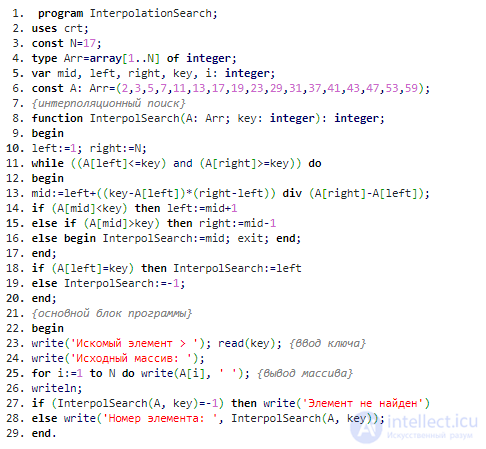
Интерполяционный поиск в эффективности, как правило, превосходит двоичный, в среднем требуя log(log(N)) операций. Тем самым время его работы составляет O(log(log(N))). Но если, к примеру, последовательность экспоненциально возрастает, то скорость увеличиться до O(N), где N (как и в предыдущем случае) – общее количество элементов в списке. Наибольшую производительность алгоритм показывает на последовательности, элементы которой распределены равномерно относительно друг друга.
Исследование, описанное в статье про интерполяционный поиск, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое интерполяционный поиск, интерполирующий поиск и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Из статьи мы узнали кратко, но содержательно про интерполяционный поиск
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов