Лекция
Привет, сегодня поговорим про хеш-таблица, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое хеш-таблица , настоятельно рекомендую прочитать все из категории Структуры данных.
| Hash table | ||
|---|---|---|
| Тип | ассоциативный массив | |
| Изобретено в | 1953 году | |
| Временная сложность в О-символике |
||
| В среднем | В худшем случае | |
| Расход памяти | O(n) | O(n) |
| Поиск | O(1) | O(n) |
| Вставка | O(1) | O(n) |
| Удаление | O(1) | O(n) |
хеш-таблица — это структура данных, реализующая интерфейс ассоциативного массива, а именно, она позволяет хранить пары (ключ, значение) и выполнять три операции: операцию добавления новой пары, операцию поиска и операцию удаления пары по ключу.
Среди всех структур данных, имеющихся в распоряжении у замечательной науки информатики, есть одна, которой многие люди восхищаются больше, чем другими. Это – хеш-таблица (Hash Table), несомненное достижение в области компьютерных наук. Практически все современные языки программирования имеют реализации хеш-таблиц в своих библиотеках. Чаще всего мы работаем с ними в виде словарей (или ассоциативных массивов), представляющих собой контейнеры множества пар ключ-значение.
Существуют два основных варианта хеш-таблиц: с цепочками и открытой адресацией. Хеш-таблица содержит некоторый массив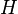 
, элементы которого есть пары (хеш-таблица с открытой адресацией) или списки пар (хеш-таблица с цепочками).
Выполнение операции в хеш-таблице начинается с вычисления хеш-функции от ключа. Получающееся хеш-значение 
играет роль индекса в массиве 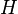. Затем выполняемая операция (добавление, удаление или поиск) перенаправляется объекту, который хранится в соответствующей ячейке массива 
.
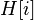Ситуация, когда для различных ключей получается одно и то же хеш-значение, называется коллизией. Такие события не так уж и редки — например, при вставке в хеш-таблицу размером 365 ячеек всего лишь 23-х элементов вероятность коллизии уже превысит 50% (если каждый элемент может равновероятно попасть в любую ячейку) — см. парадокс дней рождения. Поэтому механизм разрешения коллизий — важная составляющая любой хеш-таблицы.
В некоторых специальных случаях удается избежать коллизий вообще. Например, если все ключи элементов известны заранее (или очень редко меняются), то для них можно найти некоторую совершенную хеш-функцию, которая распределит их по ячейкам хеш-таблицы без коллизий. Хеш-таблицы, использующие подобные хеш-функции, не нуждаются в механизме разрешения коллизий, и называются хеш-таблицами с прямой адресацией.
Число хранимых элементов, деленное на размер массива 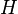(число возможных значений хеш-функции), называется коэффициентом заполнения хеш-таблицы (load factor) и является важным параметром, от которого зависит среднее время выполнения операций.
Для наглядности рассмотрим стандартные контейнеры и асимптотику их наиболее часто используемых методов.
| Контейнер \ операция | insert | remove | find |
|---|---|---|---|
| Array | O(N) | O(N) | O(N) |
| List | O(1) | O(1) | O(N) |
| Sorted array | O(N) | O(N) | O(logN) |
| Бинарное дерево поиска | O(logN) | O(logN) | O(logN) |
| Хеш-таблица | O(1) | O(1) | O(1) |
Все данные при условии хорошо выполненных контейнерах, хорошо подобранных хеш-функциях
Из этой таблицы очень хорошо понятно, почему же стоит использовать хеш-таблицы. Об этом говорит сайт https://intellect.icu . Но тогда возникает противоположный вопрос: почему же тогда ими не пользуются постоянно?
Ответ очень прост: как и всегда, невозможно получить все сразу, а именно: и скорость, и память. Хеш-таблицы тяжеловесные, и, хоть они и быстро отвечают на вопросы основных операций, пользоваться ими все время очень затратно.
Хеш-таблица — это контейнер. Реализация у него, возможно, и не очевидная, но довольно простая.
Для начала объяснение в нескольких словах. Мы определяем функцию хеширования, которая по каждому входящему элементу будет определять натуральное число. А уже дальше по этому натуральному числу мы будем класть элемент в (допустим) массив. Тогда имея такую функцию мы можем за O(1) обработать элемент.
Теперь стало понятно, почему же это именно хеш-таблица.
Важное свойство хеш-таблиц состоит в том, что, при некоторых разумных допущениях, все три операции (поиск, вставка, удаление элементов) в среднем выполняются за время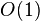 
. Но при этом не гарантируется, что время выполнения отдельной операции мало́. Это связано с тем, что при достижении некоторого значения коэффициента заполнения необходимо осуществлять перестройку индекса хеш-таблицы: увеличить значение размера массива 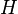и заново добавить в пустую хеш-таблицу все пары.
Вот иллюстрация хеш-таблицы. Мы видим, что индексами ключей в хеш-таблице является результат хеш-функции h, примененной к ключу.
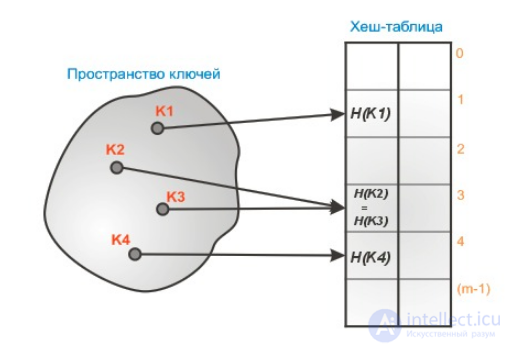
Так же этот рисунок иллюстрирует одну из основных проблем. При достаточно маленьком значении m (размера хеш-таблицы) по отношению к n (количеству ключей) или при плохой хеш-функции, может случиться так, что два ключа будут хешированны в одну и ту же ячейку массива H. Такая ситуация называется коллизией. Хорошие хеш-функции стремятся минимизировать вероятность коллизий, однако, учитывая то, что пространство всех возможных ключей может быть больше размера нашей хеш-таблицы H, все же избежать их вряд ли удастся. На этот случай имеются несколько технологий для разрешения коллизий.
Существует несколько способов разрешения коллизий.
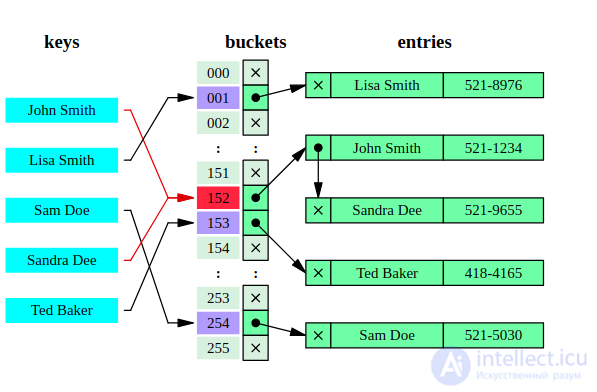
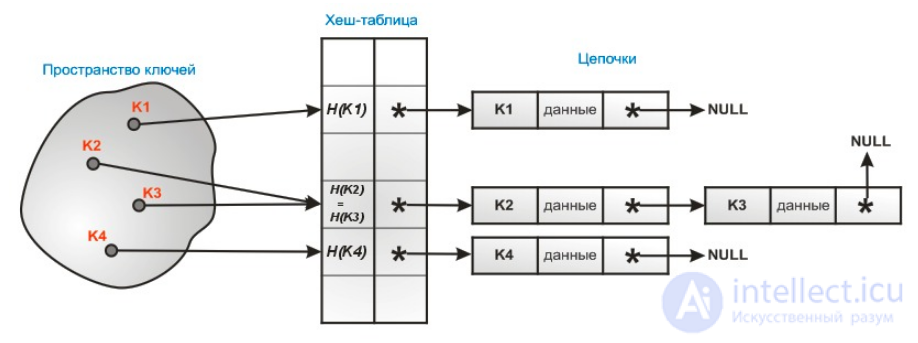
Каждая ячейка массива H является указателем на связный список (цепочку) пар ключ-значение, соответствующих одному и тому же хеш-значению ключа. Коллизии просто приводят к тому, что появляются цепочки длиной более одного элемента.
Операции поиска или удаления элемента требуют просмотра всех элементов соответствующей ему цепочки, чтобы найти в ней элемент с заданным ключом. Для добавления элемента нужно добавить элемент в конец или начало соответствующего списка, и, в случае, если коэффициент заполнения станет слишком велик, увеличить размер массива H и перестроить таблицу.
При предположении, что каждый элемент может попасть в любую позицию таблицы H с равной вероятностью и независимо от того, куда попал любой другой элемент, среднее время работы операции поиска элемента составляет Θ(1 + α), где α — коэффициент заполнения таблицы.
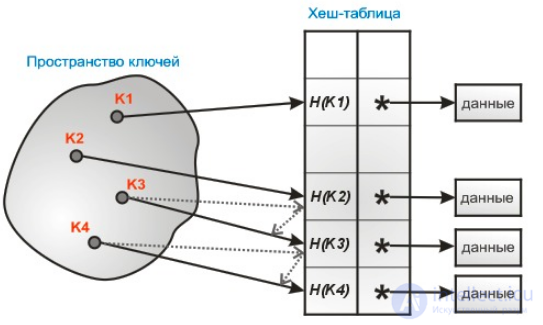
В массиве H хранятся сами пары ключ-значение. Алгоритм вставки элемента проверяет ячейки массива Hв некотором порядке до тех пор, пока не будет найдена первая свободная ячейка, в которую и будет записан новый элемент. Этот порядок вычисляется на лету, что позволяет сэкономить на памяти для указателей, требующихся в хеш-таблицах с цепочками.
Последовательность, в которой просматриваются ячейки хеш-таблицы, называетсяпоследовательностью проб. В общем случае, она зависит только от ключа элемента, то есть это последовательность h0(x), h1(x), …, hn — 1(x), где x — ключ элемента, а hi(x) — произвольные функции, сопоставляющие каждому ключу ячейку в хеш-таблице. Первый элемент в последовательности, как правило, равен значению некоторой хеш-функции от ключа, а остальные считаются от него одним из приведенных ниже способов. Для успешной работы алгоритмов поиска последовательность проб должна быть такой, чтобы все ячейки хеш-таблицы оказались просмотренными ровно по одному разу.
Алгоритм поиска просматривает ячейки хеш-таблицы в том же самом порядке, что и при вставке, до тех пор, пока не найдется либо элемент с искомым ключом, либо свободная ячейка (что означает отсутствие элемента в хеш-таблице).
Удаление элементов в такой схеме несколько затруднено. Обычно поступают так: заводят булевый флаг для каждой ячейки, помечающий, удален ли элемент в ней или нет. Тогда удаление элемента состоит в установке этого флага для соответствующей ячейки хеш-таблицы, но при этом необходимо модифицировать процедуру поиска существующего элемента так, чтобы она считала удаленные ячейки занятыми, а процедуру добавления — чтобы она их считала свободными и сбрасывала значение флага при добавлении.
Последовательности проб
Ниже приведены некоторые распространенные типы последовательностей проб. Сразу оговорим, что нумерация элементов последовательности проб и ячеек хеш-таблицы ведется от нуля, а N — размер хеш-таблицы (и, как замечено выше, также и длина последовательности проб).
hash(x) mod N, (hash(x) + 1) mod N, (hash(x) + 3) mod N, (hash(x) + 6) mod N, …
В некоторых популярных объектно-ориентированных языках программирования можно встретить методы вроде GetHashCode() и Equals() в интерфейсе корневого базового класса. Это дает возможность использовать объекты любого класса в качестве ключей хеш-таблиц. В своих классах мы переопределяем эти методы в зависимости от наших потребностей, так GetHashCode() возвращает хеш-код нашего объекта, основываясь на его внутреннем состоянии. Так, вышеупомянутые методы должны подчинятся некоторым условиям:
Так, реализация хеш-функции GetHashCode() зависит от класса объекта, и здесь мы можем использовать различные техники при расчетах.
Надеюсь, эта статья про хеш-таблица, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое хеш-таблица и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных