Привет, сегодня поговорим про методы оптимизации поиска, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
методы оптимизации поиска , настоятельно рекомендую прочитать все из категории Структуры данных.
Всегда можно говорить о некотором значении вероятности поиска того или иного элемента в таблице. Считаем, что в таблице данный элемент существует. Тогда вся таблица поиска может быть представлена как система с дискретными состояниями, а вероятность нахождения там искомого элемента - это вероятность
p(i) i - го состояния системы.
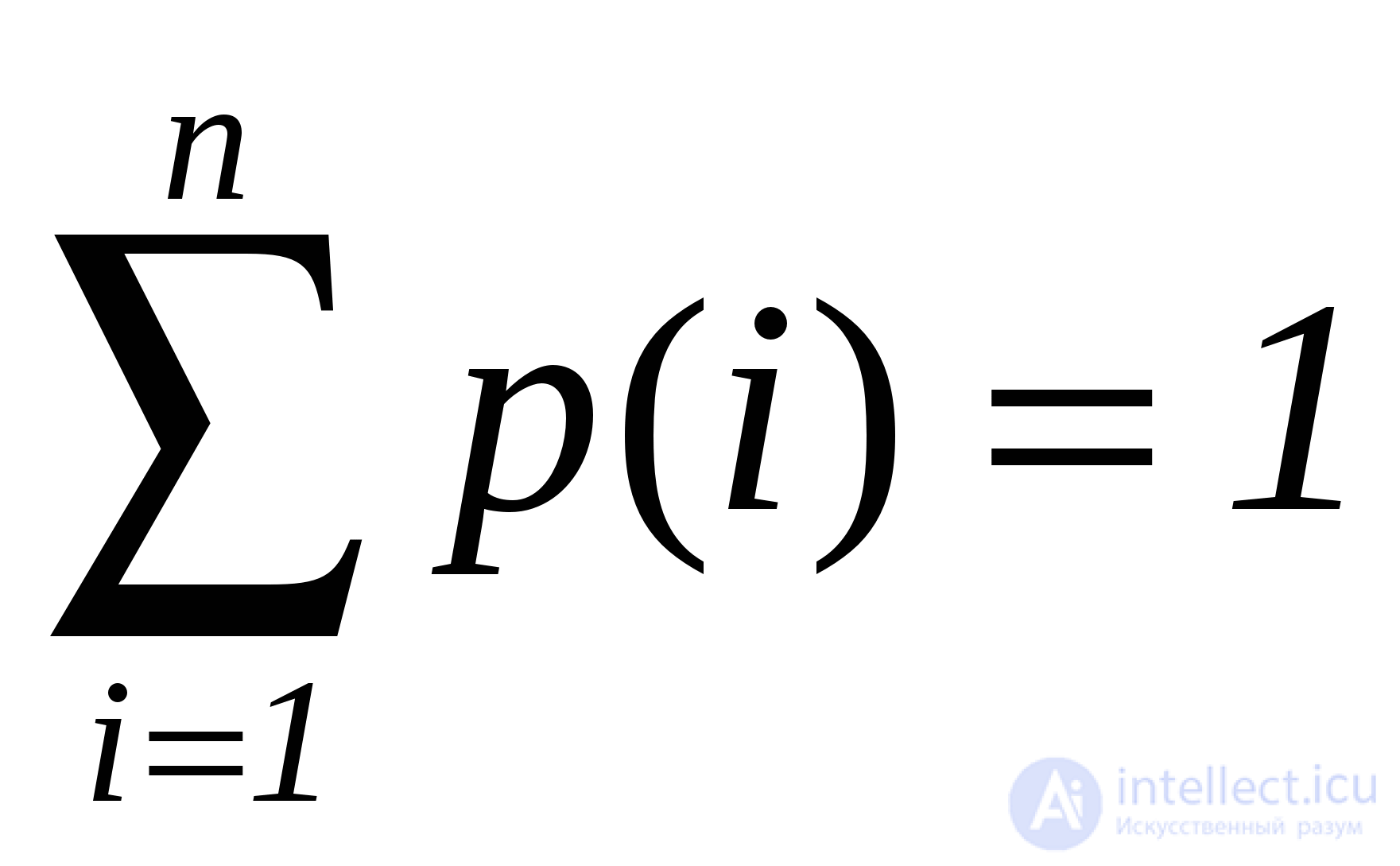
Количество сравнений при поиске в таблице, представленной как дискретная система, представляет собой математическое ожидание значения дискретной случайной величины, определяемой вероятностями состояний и номерами состояний системы.
Z=Q=1p(1)+2p(2)+3p(3)+…+np(n) Желательно, чтобы
p(1)³p(2) ³p(3) ³…³p(n).Это минимизирует количество сравнений, то есть увеличивает эффективность. Так как последовательный поиск начинается с первого элемента, то на это место надо поставить элемент, к которому чаще всего обращаются (с наибольшей вероятностью поиска).
Наиболее часто используются два основных способа автономного переупорядочивания таблиц поиска. Рассмотрим их на примере односвязных списков.
5.5.1 Переупорядочивание таблицы поиска путем перестановки найденного элемента в начало списка
Суть этого метода заключается в том, что элемент списка с ключом, равным заданному, становится первым элементом списка, а все остальные сдвигаются.
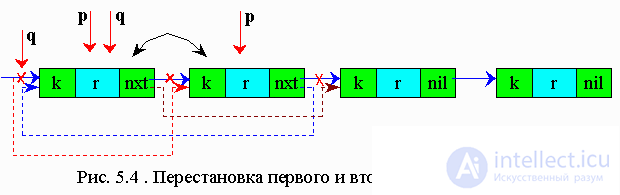
Этот алгоритм применим как для списков, так и для массивов. Однако не рекомендуется применять его для массивов, так как на перестановку элементов массива затрачивается гораздо больше времени, чем на перестановку указателей.
Алгоритм переупорядочивания в начало списка:
Псевдокод:
q=nil
p=table
while (p <> nil) do
if key = k(p) then
if q = nil then 'перестановка не нужна'
search = p
return
endif
nxt(q) = nxt(p)
nxt(p) = table
table = p
search = p
return
endif
q = p
p = nxt(p)
endwhile
search = nil
return |
Паскаль:
q:=nil;
p:=table;
while (p <> nil) do
begin
if key = p^.k then
begin
if q = nil
then 'перестановка не нужна'
search := p;
exit;
end;
q^.nxt := p^.nxt;
p^.nxt := table;
table := p;
exit;
end;
q := p;
p := p^.nxt;
end;
search := nil;
exit; |
5.5.2. Об этом говорит сайт https://intellect.icu . Метод транспозиции
В данном методе найденный элемент переставляется на один элемент к голове списка. И если к этому элементу обращаются часто, то, перемещаясь к голове списка, он скоро окажется на первом месте.
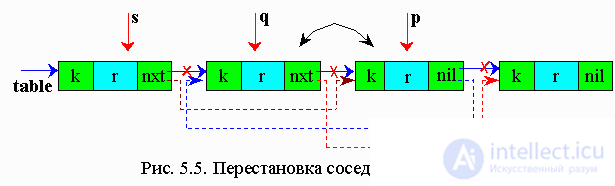
р - рабочий указатель
q - вспомогательный указатель, отстает на один шаг от р
s - вспомогательный указатель, отстает на два шага от q
Алгоритм метода транспозиции:
Псевдокод:
s=nil
q=nil
p=table
while (p <> nil) do
if key = k(p) then
‘ нашли, транспонируем
if q = nil then
‘ переставлять не надо
search=p
return
endif
nxt(q)=nxt(p)
nxt(p)=q
if s = nil then
table = p
else nxt(s)=p
endif
search=p
return
endif
endwhile
search=nil
return |
Паскаль:
s:=nil;
q:=nil;
p:=table;
while (p <> nil) do
begin
if key = p^.k then
‘ нашли, транспонируем
begin
if q = nil then
begin
‘переставлять не на-
до search:=p;
exit;
end;
q^.nxt:=p^.nxt;
p^.nxt:=q;
if s = nil then
table := p;
else
begin
s^.nxt := p;
end;
search:=p;
exit;
end;
end;
search:=nil;
exit; |
Этот метод удобен при поиске не только в списках, но и в массивах (так как меняются только два стоящих рядом элемента).
5.5.3. Дерево оптимального поиска
Если извлекаемые элементы сформировали некоторое постоянное множество, то может быть выгодным настроить дерево бинарного поиска для большей эффективности последующего поиска.
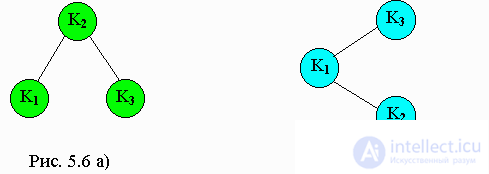
Рассмотрим деревья бинарного поиска, приведенные на рисунках a и b.Оба дерева содержат три элемента -
к1, к2, к3, где
к1<к2<к3. Поиск элемента
к3требует двух сравнений для рисунка 5.6 a), и только одного - для рисунка 5.6 б).
Число сравнений ключей, которые необходимо сделать для извлечения некоторой записи, равно уровню этой записи в дереве бинарного поиска плюс 1.
Предположим, что:
p1 - вероятность того, что аргумент поиска
key = к1 р2 - вероятность того, что аргумент поиска
key = к2р3 - вероятность того, что аргумент поиска
key = к3q0 - вероятность того, что
key < к1q1 - вероятность того, что
к2 > key > к1q2 - вероятность того, что
к3 > key > к2q3 - вероятность того, что
key > к3C1 - число сравнений в первом дереве рисунка 5.6 a)
C2 - число сравнений во втором дереве рисунка 5.6 б)
Тогда
×р1+×р2+×р3+×q0+×q1+×q2+×q3 = 1Ожидаемое число сравнений в некотором поиске есть сумма произведений вероятности того, что данный аргумент имеет некоторое заданное значение, на число сравнений, необходимых для извлечения этого значения, где сумма берется по всем возможным значениям аргумента поиска. Поэтому
C1 = 2×р1+1×р2+2×р3+2×q0+2×q1+2×q2+2×q3C2 = 2×р1+3×р2+1×р3+2×q0+3×q1+3×q2+1×q3Это ожидаемое число сравнений может быть использовано как некоторая мера того, насколько "хорошо" конкретное дерево бинарного поиска подходит для некоторого данного множества ключей и некоторого заданного множества вероятностей. Так, для вероятностей, приведенных далее слева, дерево из a) является более эффективным, а для вероятностей, приведенных справа, дерево из б) является более эффективным:
P1 = 0.1 P1 = 0.1P2 = 0.3 P2 = 0.1P3 = 0.1 P3 = 0.3q0 = 0.1 q0 = 0.1q1 = 0.2 q1 = 0.1q2 = 0.1 q2 = 0.1q3 = 0.1 q3 = 0.2C1 = 1.7 C1 = 1.9C2 = 2.4 C2 = 1.8Дерево бинарного поиска, которое минимизирует ожидаемое число сравнений некоторого заданного множества ключей и вероятностей, называется оптимальным. Хотя алгоритм создания дерева может быть очень трудоемким, дерево, которое он создает, будет работать эффективно во всех последующих поисках. К сожалению, однако, заранее вероятности аргументов поиска редко известны.
На этом все! Теперь вы знаете все про методы оптимизации поиска, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое методы оптимизации поиска
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Структуры данных
Из статьи мы узнали кратко, но содержательно про методы оптимизации поиска
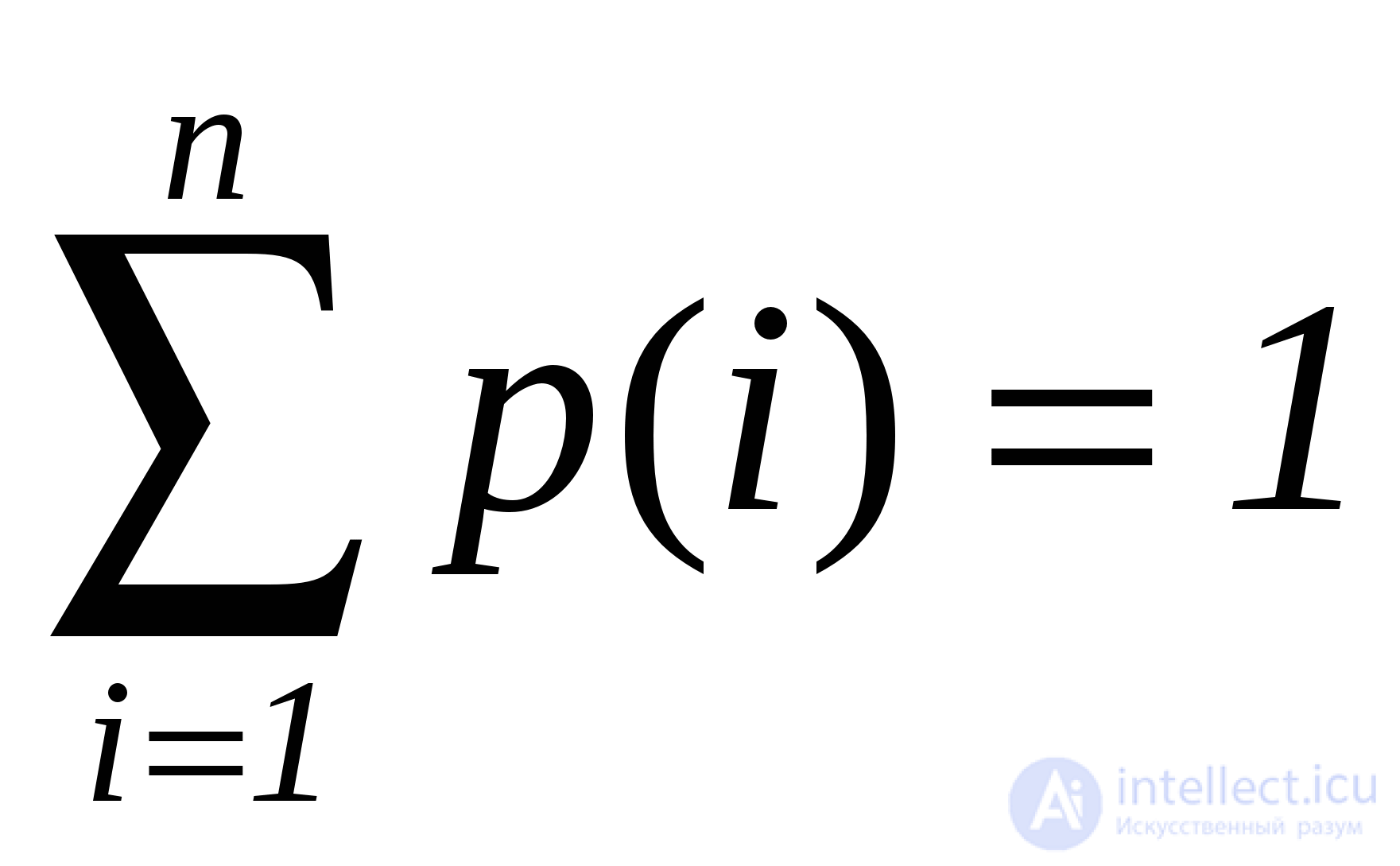



Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных