Привет, сегодня поговорим про выбор метода реализации разреженного массива в языке си, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое выбор метода реализации разреженного массива в языке си , настоятельно рекомендую прочитать все из категории Структуры данных.

ВИДЫ РАЗРЕЖЕННЫХ МАТРИЦ

Класиификация МЕТОДов ХРАНЕНИЯ РАЗРЕЖЕННЫХ МАТРИЦ

Выбор метода

При выборе одного из методов представления разреженного массива — с помощью связанного списка, двоичного дерева, массива указателей или хэширования — необходимо руководствоваться требованиями к скорости и эффективному использованию памяти. Кроме того, необходимо учесть, насколько плотно будет заполнен разреженный массив.

Если логический массив заполнен очень редко, самыми эффективными по использованию памяти оказываются связанные списки и двоичные деревья, поскольку в них память выделяется только для тех элементов, которые действительно используются. Для самих связей требуется очень небольшой дополнительный объем памяти, которым обычно можно пренебречь. Представление в виде массива указателей предполагает создание целиком всего массива из указателей, даже если некоторые элементы не используются. При этом в памяти должен не только поместиться весь массив, но еще должна остаться свободная память для работы приложения. В некоторых случаях это может быть серьезной проблемой. Обычно можно заранее оценить примерный объем свободной памяти и решить, достаточен ли он для вашей программы. Метод хэширования занимает промежуточное место между представлениями с помощью массива указателей и связанного списка или двоичного дерева. Несмотря на то, что весь первичный массив, даже если он не используется, должен находиться в памяти, этот массив все равно будет меньше, чем массив указателей.

Если логический массив будет заполнен довольно плотно, ситуация существенно меняется. В этом случае создание массива указателей и хэширование становятся более приемлемыми методами. Более того, время поиска элемента в массиве указателей постоянно и не зависит от степени заполнения логического массива. Хотя время поиска при хэшировании и не постоянно, оно ограничено сверху некоторым небольшим значением. Но в случае связанного списка и двоичного дерева среднее время поиска увеличивается по мере заполнения массива. Это следует помнить, если время доступа является критическим фактором.

Разреженные массивы.

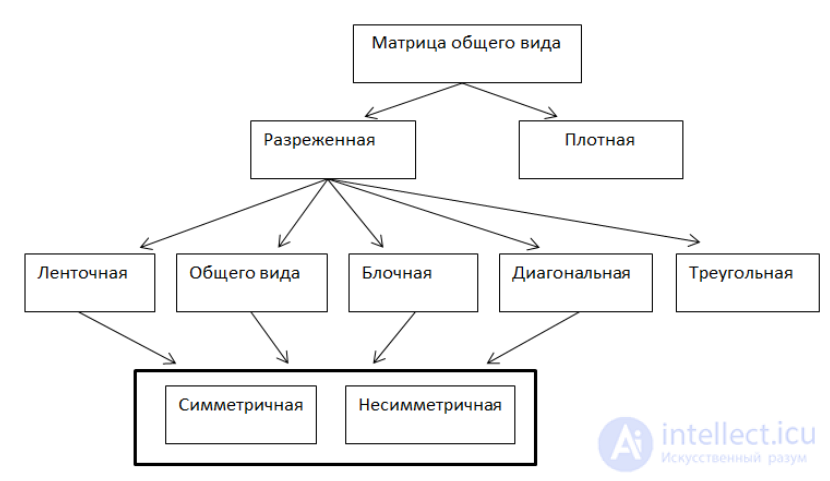
Разреженный массив - массив, большинство элементов которого равны между собой, так что хранить в памяти достаточно лишь небольшое число значений отличных от основного (фонового) значения остальных элементов.

Различают два типа разреженных массивов:

• 1) массивы, в которых местоположения элементов со значениями отличными от фонового, могут быть математически описаны;
• 2) массивы со случайным расположением элементов.

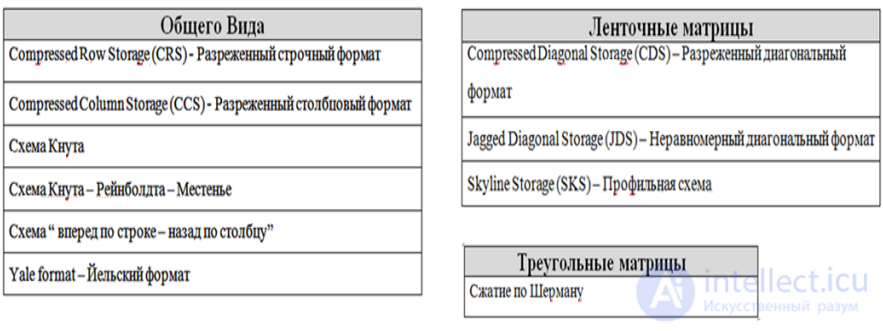
В случае работы с разреженными массивами вопросы размещения их в памяти реализуются на логическом уровне с учетом их типа.

Массивы с математическим описанием местоположения нефоновых элементов.

К данному типу массивов относятся массивы, у которых местоположения элементов со значениями отличными от фонового, могут быть математически описаны, т. е. в их расположении есть какая-либо закономерность.

Элементы, значения которых являются фоновыми, называют нулевыми; элементы, значения которых отличны от фонового, - ненулевыми. Но нужно помнить, что фоновое значение не всегда равно нулю.

Ненулевые значения хранятся, как правило, в одномерном массиве, а связь между местоположением в исходном, разреженном, массиве и в новом, одномерном, описывается математически с помощью формулы, преобразующей индексы массива в индексы вектора.

На практике для работы с разреженным массивом разрабатываются функции:

• а) для преобразования индексов массива в индекс вектора;
• б) для получения значения элемента массива из ее упакованного представления по двум индексам (строка, столбец);
• в) для записи значения элемента массива в ее упакованное представление по двум индексам.

При таком подходе обращение к элементам исходного массива выполняется с помощью указанных функций. Например, пусть имеется двумерная разреженная матрица, в которой все ненулевые элементы расположены в шахматном порядке, начиная со второго элемента. Для такой матрицы формула вычисления индекса элемента в линейном представлении будет следующей : L=((y-1)*XM+x)/2), где L - индекс в линейном представлении; x, y - соответственно строка и столбец в двумерном представлении; XM - количество элементов в строке исходной матрицы.

В программном примере 3.1 приведен модуль, обеспечивающий работу с такой матрицей (предполагается, что размер матрицы XM заранее известен).

 {===== Программный пример 3.1 =====}  Unit ComprMatr;
 Interface
  Function PutTab(y,x,value : integer) : boolean;
  Function GetTab(x,y: integer) : integer;
 Implementation
  Const XM=...;
  Var arrp: array[1..XM*XM div 2] of integer;
  Function NewIndex(y, x : integer) : integer;
     var  i: integer;
     begin   NewIndex:=((y-1)*XM+x) div 2);  end;
  Function PutTab(y,x,value : integer) : boolean;
     begin
        if NOT ((x mod 2<>0) and (y mod 2<>0)) or
           NOT ((x mod 2=0) and (y mod 2=0))  then begin
              arrp[NewIndex(y,x)]:=value;  PutTab:=true; end
                                              else PutTab:=false;
     end;
  Function GetTab(x,y: integer) : integer;
     begin
        if ((x mod 2<>0) and (y mod 2<>0)) or
           ((x mod 2=0) and (y mod 2=0)) then GetTab:=0
        else GetTab:=arrp[NewIndex(y,x)];
     end;
end.

Сжатое представление матрицы хранится в векторе arrp.

Функция NewIndex выполняет пересчет индексов по вышеприведенной формуле и возвращает индекс элемента в векторе arrp.

Функция PutTab выполняет сохранение в сжатом представлении одного элемента с индексами x, y и значением value. Сохранение выполняется только в том случае, если индексы x, y адресуют не заведомо нулевой элемент. Если сохранение выполнено, функция возвращает true, иначе - false.

Для доступа к элементу по индексам двумерной матрицы используется функция GetTab, которая по индексам x, y возвращает выбранное значение. Если индексы адресуют заведомо нулевой элемент матрицы, функция возвращает 0.

Обратите внимание на то, что массив arrp, а также функция NewIndex не описаны в секции IMPLEMENTATION модуля. Доступ к содержимому матрицы извне возможен только через входные точки PutTab, GetTab с заданием двух индексов.

В программном примере 3.2 та же задача решается несколько иным способом: для матрицы создается дескриптор - массив desc, который заполняется при инициализации матрицы таким образом, что i-ый элемент массива desc содержит индекс первого элемента i-ой строки матрицы в ее линейном представлении. Процедура инициализации InitTab включена в число входных точек модуля и должна вызываться перед началом работы с матрицей. Но доступ к каждому элементу матрицы (функция NewIndex) упрощается и выполняется быстрее: по номеру строки y из дескриптора сразу выбирается индекс начала строки и к нему прибавляется смещение элемента из столбца x. Процедуры PutTab и GetTab - такие же, как и в примере 3.1 поэтому здесь не приводятся.

 {===== Программный пример 3.2 =====}
 Unit ComprMatr;
 Interface
  Function PutTab(y,x,value : integer) : boolean;
  Function GetTab(x,y: integer) : integer;
  Procedure InitTab;
 Implementation
  Const XM=...;
  Var arrp: array[1..XM*XM div 2] of integer;
      desc: array[1..XM] of integer;
  Procedure InitTab;
  var i : integer;
   begin
      desc[1]:=0;  for i:=1 to XM do desc[i]:=desc[i-1]+XM;
   end;
  Function NewIndex(y, x : integer) : integer;
  var  i: integer;
  begin  NewIndex:=desc[y]+x div 2;  end;
end. Об этом говорит сайт https://intellect.icu  . 

Разреженные массивы со случайным расположением элементов.

К данному типу массивов относятся массивы, у которых местоположения элементов со значениями отличными от фонового, не могут быть математически описаны, т. е. в их расположении нет какой-либо закономерности.

Ё 0  0  6  0  9  0  0 Ё
Ё 2  0  0  7  8  0  4 Ё
Ё10  0  0  0  0  0  0 Ё
Ё 0  0 12  0  0  0  0 Ё
Ё 0  0  0  3  0  0  5 Ё

Пусть есть матрица А размерности 5*7, в которой из 35 элементов только 10 отличны от нуля.

Представление разреженным матриц методом последовательного размещения.

Один из основных способов хранения подобных разреженных матриц заключается в запоминании ненулевых элементов в одномерном массиве и идентификации каждого элемента массива индексами строки и столбца, как это показано на рис. 3.5 а).

Доступ к элементу массива A с индексами i и j выполняется выборкой индекса i из вектора ROW, индекса j из вектора COLUM и значения элемента из вектора A. Слева указан индекс k векторов наибольшеее значение, которого определяется количеством нефоновых элементов. Отметим, что элементы массива обязательно запоминаются в порядке возрастания номеров строк.

Более эффективное представление, с точки зрения требований к памяти и времени доступа к строкам матрицы, показано на рис.3.5.б). Вектор ROW уменьшнен, количество его элементов соответствует числу строк исходного массива A, содержащих нефоновые элементы. Этот вектор получен из вектора ROW рис. 3.5.а) так, что его i-й элемент является индексом k для первого нефонового элемента i-ой строки.

Представление матрицы А, данное на рис. 3.5 сокращает требования к объему памяти более чем в 2 раза. Для больших матриц экономия памяти очень важна. Способ последовательного распределения имеет также то преимущество, что операции над матрицами могут быть выполнены быстрее, чем это возможно при представлении в виде последовательного двумерного массива, особенно если размер матрицы велик.

Рис. 3.5. Последовательное представление разреженных матриц.

Представление разреженных матриц методом связанных структур.

Методы последовательного размещения для представления разреженных матриц обычно позволяют быстрее выполнять операции над матрицами и более эффективно использовать память, чем методы со связанными структурами. Однако последовательное представление матриц имеет определенные недостатки. Так включение и исключение новых элементов матрицы вызывает необходимость перемещения большого числа других элементов. Если включение новых элементов и их исключение осуществляется часто, то должен быть выбран описываемый ниже ме- тод связанных структур.

Метод связанных структур, однако, переводит представляемую структуру данных в другой раздел классификации. При том, что логическая структура данных остается статической, физическая структура становится динамической.

Для представления разреженных матриц требуется базовая структура вершины (рис.3.6), называемая MATRIX_ELEMENT ("элемент матрицы"). Поля V, R и С каждой из этих вершин содержат соответственно значение, индексы строки и столбца элемента матрицы. Поля LEFT и UP являются указателями на следующий элемент для строки и столбца в циклическом списке, содержащем элементы матрицы. Поле LEFT указывает на вершину со следующим наименьшим номером строки.

Рис.3.6. Формат вершины для представления разреженных матриц

На рис. 3.7 приведена многосвязная структура, в которой используются вершины такого типа для представления матрицы А, описанной ранее в данном пункте. Циклический список представляет все строки и столбцы. Список столбца может содержать общие вершины с одним списком строки или более. Для того, чтобы обеспечить использование более эффективных алгоритмов включения и исключения элементов, все списки строк и столбцов имеют головные вершины. Головная вершина каждого списка строки содержит нуль в поле С; аналогично каждая головная вершина в списке столбца имеет нуль в поле R. Строка или столбец, содержащие только нулевые элементы, представлены головными вершинами, у которых поле LEFT или UP указывает само на себя.

Рис. 3.7. Многосвязная структура для представления матрицы A

Может показаться странным, что указатели в этой многосвязной структуре направлены вверх и влево, вследствие чего при сканировании циклического списка элементы матрицы встречаются в порядке убывания номеров строк и столбцов. Такой метод представления используется для упрощения включения новых вершин в структуру. Предполагается, что новые вершины, которые должны быть добавлены к матрице, обычно располагаются в порядке убывания индексов строк и индексов столбцов. Если это так, то новая вершина всегда добавляется после головной и не требуется никакого просмотра списка.

Под разреж ен н ы м м ассивом понимается массив относительно
большого объема (например, состоящий из нескольких миллионов элементов), большинство элементов которого равны одному и тому же значению (чаще всего нулю) и лишь некоторые элементы, количество которых ничтожно в сравнении с размером массива, от этого значения отличаются. Естественно, в такой ситуации целесообразно хранить в памяти
лишь те элементы массива, значения которых отличны от нуля (или другого значения, которому равно большинство элементов).
Попробуем написать на С и ++ такой класс, который ведет себя как целочисленный массив потенциально бесконечного размера9 в том смысле,
что к объекту этого класса применима операция индексирования (квадратные скобки), однако объект реально хранит только те элементы, значения которых отличаются от нуля. Назовем этот класс SparseArraylnt.
Для простоты картины будем считать, что количество ненулевых элементов массива настолько незначительно, что даже линейный поиск среди них может нас устроить по быстродействию. Это позволит хранить
ненулевые элементы массива в виде списка пар «индекс/значение». Все
детали реализации, включая и структуру, представляющую звено списка, скроем в приватной части класса. Это позволит при необходимости
сменить реализацию на более сложную.
Основная проблема при реализации разреженного массива возникает
в связи с поведением операции индексирования. Дело в том, что выражение «элемент массива» может встречаться как в правой, так и в
левой части присваиваний, и в обоих случаях используется одна и та
же функция-метод класса SparseArraylnt, называемая operator [] . Если бы все элементы массива хранились в памяти (как это было в примере
из §2.19.2), можно было бы просто возвратить ссылку на соответствующее место в памяти, где хранится элемент, соответствующий заданному
индексу. С разреженным массивом так действовать не получится, поскольку в большинстве случаев элемент в памяти не хранится. Однако
же просто возвратить нулевое значение (без всякой ссылки) нельзя, ведь
это означало бы, что выражение, содержащее нашу операцию индексирования, нельзя применять в левой части присваивания.
Итак, что же делать в случае, если операция индексирования вызвана
для индекса, для которого соответствующий элемент в памяти не хра

9На самом деле мы будем использовать в качестве индекса тип unsigned long;
значения этого типа могут достигать 232 - 1, т. е. чуть больше четырех миллиардов.

нится, поскольку равен нулю? Одно из возможных решений — завести в
памяти соответствующий элемент, пусть даже и с нулевым значением, и
вернуть соответствующую ссылку. Это позволит, безусловно, выполнять
присваивания, однако приведет к тому, что при каждом обращении к
нулевым элементам (в том числе на чтение, а не на запись) соответствующие элементы будут заводиться в памяти и, таким образом, окажется,
что изрядное количество памяти занято теми самыми нулевыми значениями, хранения которых можно избежать.
Схему можно несколько усовершенствовать, если каждый раз при вызове операции индексирования сохранять в приватной части объекта значение индекса или даже адрес заводимого звена списка. Это позволит при
следующем вызове проверить, хранит ли запись, заведенная на предыдущем вызове, число, отличное от нуля, и если нет, то удалить ее, освободив
память. У такого варианта реализации есть, однако, свой недостаток: на
заведение и удаление элементов будет тратиться изрядное количество
времени.
Очевидно, было бы великолепно иметь возможность вызывать разные
функции-методы для случаев, когда происходит обращение к элементу
массива на чтение и когда индексирование используется для присваивания элементу нового значения. В первом случае можно было бы тогда
возвращать просто значение элемента или ноль, если соответствущего
элемента в памяти нет; во втором случае можно было бы без особых
проблем создавать новый элемент и возвращать ссылку на поле, хранящее значение; это, впрочем, не исключает необходимости проверки на
следующем вызове, не оказался ли в соответствующем элементе ноль.
К сожалению, такой возможности в Си-|—Ь нет, как нет и возможности определить из тела операции индексирования, вызвана она из левой
части присваивания или нет10. Соответствующую возможность, однако,
можно смоделировать. Никто не мешает нам описать небольшой вспомогательный класс, объекты которого как раз и будет возвращать наша
операция индексирования. Такой вспомогательный объект будет просто
хранить всю имеющую отношение к делу информацию, а в нашем случае такой информации немного: адрес главного объекта (то есть самого
разреженного массива), с которым нужно работать, и значение индекса,
переданное в качестве параметра операции индексирования.
Имея эту информацию и соответствующий доступ к объекту массива,
наш вспомогательный объект в зависимости от ситуации может произвести любые действия, которые в этой ситуации могут потребоваться. Что
же касается определения, какая из возможных ситуаций имеет место, то
у вспомогательного объекта для этого есть существенно больше возможностей, чем было в теле операции индексирования: ведь все операции,

"'Это вполне можно считать недостатком СиН— . однако критика имеющегося языка
выходит за рамки данного пособия.
6применяемые к результату операции индексирования, как раз и будут на
самом деле применены к этому объекту. Таким образом, достаточно, например, определить для нашего вспомогательного класса операции преобразования к типу in t и присваивания, чтобы сделать возможным и
корректным следующий код:
SparseArrayInt a rr;
int x;
/ / . . .
x = a r r [500]; / / чтение
a r r [300] = 5 0 ; / / запись (возможно создание элемента)
a r r [200] = 0 ; / / удаление элемента, если таковой есть
К сожалению, у такой реализации есть и недостаток. Дело в том, что
обычное присваивание — это далеко не единственная операция, способная изменить значение целочисленной переменной. Пользователь вполне
может попытаться использовать, например, такие выражения:
a r r [15] += 100;
х = a r r [200]++;
у = - - a r r [200];
Чтобы все подобные операции работали, нам придется для нашего вспомогательного объекта определить их все явным образом, что потребует
изрядного объема работы: языки Си и С и ++ поддерживают десять операций присваивания, совмещенных с арифметическими действиями (+=,
-=, <<= и т. п.), плюс к тому четыре операции инкремента/декремента
(++ и -- в префиксной и постфиксной форме). В нашем примере мы
ограничимся описанием операции += и двух форм операции ++. Остальные подобные операции читатель без труда опишет самостоятельно по
аналогии.
Прежде чем продемонстрировать заголовок класса Spar seArray Int,
отметим, что для удобства реализации всех модифицирующих операций
целесообразно в классе вспомогательного объекта ввести две внутренние
функции. Функция Provide будет отыскивать в списке элемент, соответствующий заданному индексу, и возвращать ссылку на поле, содержащее
значение; если соответствующего элемента в списке нет, функция будет
его создавать. Вторая функция, Remove, будет удалять из списка элемент
с заданным индексом, если таковой в списке присутствует. Вспомогательный класс назовем Interm от английского intermediate. С учетом этого
заголовок класса будет выглядеть так:
class SparseArraylnt {
struct Item {
int index;

in t v a lu e ;
Item *n e x t;
};
Item * f i r s t ;
p u b lic :
Sp arseA rray ln t() : fir s t(O ) { }
"S p arse A rray ln t( ) ;
c la s s Interm {
frie n d c la s s SparseA rrayln t;
SparseA rraylnt *m a ste r;
in t in d ex;
Interm (SparseA rrayln t *a_m aster, in t ind)
: m aster(a_ m aster), in dex(in d) { }
int& P ro v id e(in t id x ) ;
void Remove(int id x );
p u b lic :
operator i n t ( ) ;
in t o p e rato r= (in t x ) ;
in t o p erato r+ = (in t x ) ;
in t o p e ra to r+ + ();
in t o p e ra to r+ + (in t);
};
frie n d c la s s Interm;
Interm o p e ra to r (in t idx)
{ retu rn In te rm (th is, id x ); }
p r iv a t e :
S p arseA rray ln t(co n st SparseArrayInt& ) { }
void o p erato r=(co n st SparseArrayInt& ) { }
В самом классе SparseArraylnt, как можно заметить, оказывается не
так много функций: основная функциональность оказывается вытеснена в методы вспомогательного класса. Единственным методом основного
класса, тело которого в силу размеров не включено в заголовок класса,
является его деструктор. Его задача — освободить память от элементов
списка. Деструктор описывается так:
SparseA rraylnt: : "SparseA rraylnt() {
w h ile (first) {
Item *tmp = f i r s t ;
f i r s t = first-> n e x t;
delete tmp;
}Опишем теперь методы класса SparseArray: : Interm, в которых и заключается основная функциональность нашего разреженного массива:
in t S p arseA rray In t: : In term :: o p e rato r= (in t x)
{
i f ( x == 0) {
Rem ove(index);
} e ls e {
P rovide(in dex) = x;
}
retu rn x;
}
in t S p arseA rray In t: : In term :: o p erato r+ = (in t x)
{
int& lo c a tio n = P ro v id e(in d ex );
lo c a tio n += x;
in t r e s = lo c a tio n ;
i f ( r e s == 0) Rem ove(index);
retu rn r e s ;
}
in t S p arseA rray In t: : In term ::o p erato r+ + ()
{
int& lo c a tio n = P ro v id e(in d ex );
in t r e s = + + lo c atio n ;
if ( lo c a t io n == 0) Rem ove(index);
retu rn r e s ;
}
in t S p arseA rray In t: : In term :: o p erato r+ + (in t)
{
int& lo c a tio n = P ro v id e(in d ex );
in t r e s = lo catio n + + ;
if ( lo c a t io n == 0) Rem ove(index);
retu rn r e s ;
}
S p arseA rray In t: : In term :: operator in t()
{
Item * tmp;
for(tm p = m a s t e r - > f ir s t ; tmp; tmp = tmp->next) {
if(tm p ->in dex == index) {
retu rn tm p->value;
}
}
retu rn 0;
}
Наконец, опишем вспомогательные функции Provide и Remove:
int& S p arseA rray In t: : In term ::P ro v id e(in t idx)

{
Item * tmp;
for(tm p = m a s t e r - > f ir s t ; tmp; tmp = tmp->next) {
if(tm p->in dex == index)
retu rn tm p->value;
}
tmp = пей Item;
tmp->index = index;
tmp->next = m a s te r - > fir s t;
m a ste r - > fir st = tmp;
retu rn tm p->value;
}
void S p arseA rray ln t: : In term ::Remove(int idx)
{
Item ** tmp;
for(tm p = & (m a ste r - > fir st); *tm p; tmp = &(*tm p)->next)
{
i f ( (*tm p)->index == index) {
Item *to _ d e le te = *tmp;
*tmp = (*tm p)->next;
d e le te to _ d e le te ;
retu rn ;
}
}

}

Надеюсь, эта статья про выбор метода реализации разреженного массива в языке си, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое выбор метода реализации разреженного массива в языке си и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.