Лабораторная работа №11. "ИССЛЕДОВАНИЕ МЕТОДОВ ОПТИМИЗАЦИИ ПОИСКА "

Привет, сегодня поговорим про исследование методов оптимизации поиска, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое исследование методов оптимизации поиска , настоятельно рекомендую прочитать все из категории Структуры данных.

Цель работы: исследовать и изучить методы поиска с перемещением в начало и транспозицией.


Задача работы: овладеть навыками написания программ по исследованию методов поиска с перемещением в начало и транспозицией на языке программирования ПАСКАЛЬ .


Порядок работы :

• 
  изучить описание лабораторной работы;

• 
  по заданию, данному преподавателем, разработать алгоритм программы решения задачи;

• 
  написать программу на языке ПАСКАЛЬ;

• 
  отладить программу;

• 
  решить задачу;

• 
  оформить отчет.

Краткая теория

ПОИСК (SEARCH) является одной из основ обработки данных в ЭВМ. Его назначение состоит в том, чтобы по заданному аргументу найти среди массива данных те данные, которые соответствуют этому аргументу или определить, что этих данных нет. Если этих данных нет, добавить их в массив данных.

Набор любых данных будем называть ТАБЛИЦЕЙ или ФАЙЛОМ. Данное или элемент структуры отличается каким-то признаком от других данных. Этот признак называется КЛЮЧОМ. Ключ может быть УНИКАЛЬНЫМ, т.е. в таблице только одно данное с таким ключом, иначе уникальные ключи называются ПЕРВИЧНЫМИ КЛЮЧАМИ.

ВТОРИЧНЫЙ КЛЮЧ в одной таблице может повторяться, но по нему тоже можно организовать поиск. Ключи данных собраны в одном месте (таблице).

Ключи, которые выделены из таблицы данных и организованы в свой файл, называются ВНЕШНИМИ КЛЮЧАМИ. Если ключ в записи, то он называется ВНУТРЕННИМ КЛЮЧОМ.

ПОИСКОМ ПО ЗАДАННОМУ АРГУМЕНТУ называется алгоритм, определяющий соответствие ключа данного с заданным аргументом. Результатом работы алгоритма поиска может быть нахождение этого данного или отсутствие данного в таблице. В случае отсутствия данного возможны две операции:

1. Индикация того, что данного нет.

2. Вставка данного в таблицу.

Пусть К - массив ключей, тогда для всех К(i) существует R(i) - данное. KEY - аргумент поиска. Ему соответствует информационная запись REC. В зависимости от того, какова структура данных в таблице, различают несколько видов поиска.


ПЕРЕУПОРЯДОЧЕНИЕ ТАБЛИЦЫ ПОИСКА


Всегда можно говорить о некотором значении вероятности нахождения того или иного элемента.

P(i) - вероятность нахождения элемента.

В этом случае таблица поиска представляется как система с дискретными состояниями, а искомый элемент характеризуется i-ым состоянием системы, вероятность которого P(i).

P(1) + P(2) + ... Об этом говорит сайт https://intellect.icu . + P(n) = 1

Количество сравнений Z при поиске в таблице, т.е. количество сравнений, необходимых для поиска по заданному аргументу, представляет собой значение дискретной случайной величины, определяемой номерами состояний и вероятностями состояний системы.

Z=1*P(1) + 2*P(2) + 3*P(3) + ... + n*P(n)


ТАБЛИЦА ДАННЫХ ДОЛЖНА БЫТЬ УПОРЯДОЧЕНА ТАКИМ ОБРАЗОМ , чтобы в начале таблицы были элементы с большими вероятностями поиска или элементы , к которым чаще всего обращаются в таблице.

P(1) >= P(2) >= P(3) >= ... >= P(n)


ИМЕЕТСЯ ДВА ОСНОВНЫХ МЕТОДА ПЕРЕУПОРЯДОЧЕНИЯ ТАБЛИЦ ПОИСКА:

1. 
   Переупорядочение путем перестановки найденного элемента в начало списка.
2. 
   Метод транспозиции.

Алгоритм

Переупорядочение путем перестановки в начало списка

Найденный элемент сразу оказывается в голове списка. 


Первоначально указатель q нулевой, указатель p указывает на начало списка; p перемещается на второй элемент, а q на первый. Указатель начала списка (table) перемещается на второй элемент, а указатель второго элемента на третий. Таким образом второй элемент перемещается на первое место. 


(ПСЕВДОКОД)

q=nil 

p=table 

WHILE (p <> nil) do 

IF key=k(p)

then SEARCH=p

next(q)=next(p)

next(p)=q

table=p

return

end IF

q=p

p=next(p)

end WHILE

SEARCH=0

return

Метод транспозиции

В данном методе найденный элемент переставляется на один элемент к голове списка. Если к этому элементу обращаются часто, то постепенно перемещаясь к началу списка, он скоро окажется в его голове. 

Этот метод удобен тем, что он эффективен не только в списковых структурах, но и в неупорядоченных массивах, т.к. меняются местами только два рядом стоящих элемента. 

Будем использовать три указателя: 

p - рабочий указатель, указывает на элемент. 

q - вспомогательный указатель, отстает на один шаг от p. 


s - вспомогательный указатель, отстает на два шага от p.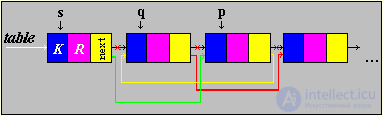





Найденный нами третий элемент передвигается на один шаг к голове списка (т.е. становится вторым). Указатель первого элемента перемещается на третий элемент, указатель второго элемента на четвертый, таким образом третий элемент перемещается на второе место. Если к данному элементу обратиться еще раз, то он окажется в голове списка.


s=nil

q=nil

p=nil

while (p<>nil) do

if key=k(p) then search=p

if q=nil then return

else next(q)=next(p)

next(p)=q

if s=nil then table

else next(s)=p

end if

search=p

end if

end if

return

end while

search=nil return

Задания

Дан массив целых чисел. Составить процедуры метода транспозиции и перестановки в начало. Решить заданную задачу и переставить найденный в задаче элемент обоими методами в начало списка.


ВАРИАНТ 1. Найти максимальный элемент массива.


ВАРИАНТ 2. Найти минимальный элемент массива.


ВАРИАНТ 3. Найти число, нацело делящееся на 11 ( если таких чисел несколько, то найти максимальное; если таких чисел нет - выдать сообщение ).


ВАРИАНТ 4. Найти число, нацело делящееся на 11 ( если таких чисел несколько, то найти максимальное; если таких чисел нет - выдать сообщение ).


ВАРИАНТ 5. Найти элемент, разность соседних элементов которого не меньше 72. Если таких элементов несколько, выбрать максимальный. Если таких элементов нет, выдать сообщение.


ВАРИАНТ 6. Найти элемент, частное соседних элементов которого четное число. Если таких элементов несколько, выбрать максимальный или минимальный элемент. Если таких элементов нет, выдать сообщение.


ВАРИАНТ 7. Найти элемент, разность соседних элементов которого четное число. Если таких элементов несколько, выбрать максимальный или минимальный элемент. Если такого элемента нет, выдать сообщение.


ВАРИАНТ 8. Найти элемент, среднее арифметическое элементов, находящихся до этого элемента равно 12. Если таких элементов нет, выдать сообщение.


ВАРИАНТ 9. Найти максимальный элемент, делящийся на 10. Если такого элемента нет, выдать сообщение.


ВАРИАНТ 10. Найти элемент, разность соседних элементов которого четное число и делится на 3. Если такого элемента нет, выдать сообщение.


ВАРИАНТ 11. Найти элемент, среднее квадратичное элементов, находящихся после этого элемента меньше 10. Если таких элементов несколько, выбрать максимальный элемент. Если таких элементов нет, выдать сообщение.


ВАРИАНТ 12. Найти значение tg (x) от каждого элемента и переставить на 1 место элемент, значение функции от которого максимально.

На этом все! Теперь вы знаете все про исследование методов оптимизации поиска, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое исследование методов оптимизации поиска и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных