Лекция
Привет, сегодня поговорим про сортировка методом прямого выбора, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое сортировка методом прямого выбора, сортировка , настоятельно рекомендую прочитать все из категории Структуры данных.
В общем сортировку следует понимать как процесс перегруппировки заданного множества объектов в некотором определенном порядке. Цель сортировки облегчить последующий поиск элементов в таком отсортированном множестве. Это почти универсальная, фундаментальная деятельность. Мы встречаемся с отсортированными объектами в телефонных книгах, в списках подоходных налогов, в оглавлениях книг, в библиотеках, в словарях, на складах почти везде, где нужно искать хранимые объекты. Даже малышей учат держать свои вещи "в порядке", и они уже сталкиваются с некоторыми видами сортировок задолго до того, как познакомятся с азами арифметики.
Таким образом, разговор о сортировке вполне уместен и важен, если речь идет об обработке данных. Что может легче сортироваться, чем данные? Тем не менее наш первоначальный интерес к сортировке основывается на том, что при построении алгоритмов мы сталкиваемся со многими весьма фундаментальными приемами. Почти не существует методов, с которыми не приходится встречаться при обсуждении этой задачи. В частности,
сортировка это идеальный объект для демонстрации огромного разнообразия алгоритмов, все они изобретены для одной и той же задачи, многие в некотором смысле оптимальны, большинство имеет свои достоинства. Поэтому это еще и идеальный объект, демонстрирующий необходимость анализа производительности алгоритмов. К тому же на примерах сортировок можно показать, как путем усложнения алгоритма, хотя под рукой и есть уже очевидные методы, можно добиться значительного выигрыша в эффективности.
Выбор алгоритма зависит от структуры обрабатываемых данных это почти закон, но в случае сортировки такая зависимость столь глубока, что соответствующие методы были даже разбиты на два класса сортировку массивов и сортировку файлов последовательностей . Иногда их называют внутренней и внешней сортировкой, поскольку массивы хранятся в быстрой оперативной, внутренней памяти машины со случайным доступом, а файлы обычно размещаются в более медленной, но и более емкой внешней памяти, на устройствах, основанных на механических перемещениях дисках или лентах . Об этом говорит сайт https://intellect.icu . Уже на примере сортировки пронумерованных карточек становится очевидным существенное различие в этих подходах. Если карты "выстроены" в виде массива, то они как бы лежат перед сортирующим, он видит каждую из них и имеет к ней доступ. Если же карты образуют файл, то это предполагает, что видна только верхняя карта в каждой из стопок. Такое ограничение, конечно же, серьезно повлияет на метод сортировки, но ничего не поделаешь: ведь карточек может быть так много, что все они на столе не поместятся.
Прежде чем идти дальше, введем некоторые понятия и обозначения. Ими мы будем пользоваться далее. Если у нас есть элементы а1, а2,..., аn, то сортировка есть перестановка этих элементов массив ак1, ак2, ..., акn, где при некоторой упорядочивающей функции f выполняются отношения f аk1 <= f аk2 <= ... <= f аkn.
Обычно упорядочивающая функция не вычисляется по какому-либо правилу, а хранится как явная компонента поля каждого элемента. Ее значение называется ключом кеу элемента. Поэтому для представления элементов хорошо подходят такие образования, как запись, а графически это представляется так (рис. 1):
Говоря об алгоритмах сортировки, мы будем обращать внимание лишь на компоненту - ключ, другие же компоненты можно даже и не определять (рис.2). Поэтому из наших дальнейших рассмотрений вся сопутствующая информация. Чтобы уменьшить эти затраты, сортировку производят в таблице адресов ключей. После сортировки перестанавливают указатели. Это метод сортировки таблицы адресов (рис.3) . Метод сортировки называется устойчивым, если в процессе сортировки относительное расположение элементов с равными ключами не изменяется. Устойчивость сортировки часто бывает желательной, если речь идет об элементах, уже упорядоченных (отсортированных) по некоторым вторичным ключам (т.е. свойствам) , не влияющим на основной ключ. 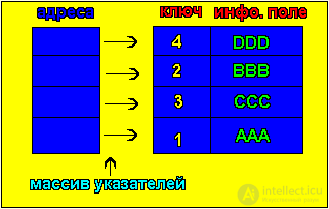
Отсортированный массив (рис. 2):
Массив отсортированный другим методом (рис. 3):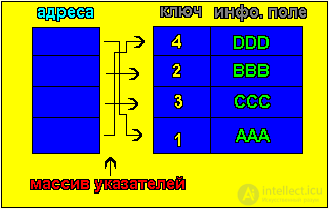
Основное условие: выбранный метод сортировки массивов должен экономно использовать доступную память. Это предполагает, что перестановки, приводящие элементы в порядок, должны выполняться на том же месте, т.е. методы, в которых элементы из массива А передаются в результирующий массив H, представляют существенно меньший интерес. Ограничив критерием экономии памяти наш выбор нужного метода среди многих возможных, мы будем сначала классифицировать методы по их экономичности, т.е. по времени их работы. Хорошей мерой эффективности может быть С - число необходимых сравнений ключей и М - число пересылок (перестановок) элементов.
Эти числа - функции от n- числа сортируемых элементов. Хотя улучшенные алгоритмы сортировки требуют порядка n*log n сравнений, мы разберем простой метод, который причисляется к так называемым прямым, где требуется порядка n^2 сравнений ключей. К достоинствам прямых методов относятся :
1.Прямые методы особенно удобны для объяснения характерных черт основных принципов большинства сортировок.
2.Программы этих методов легко понимать, и они коротки. Напомним, что сами программы также занимают память.
3.Улучшенные методы требуют небольшого числа операций, но эти операции обычно сами более сложны, и поэтому для достаточно малых n прямые методы оказываются быстрее, хотя при больших n их использовать, конечно, не следует.
Методы сортировки "на том же месте" можно разбить в соответствии с определяющими их принципами на три основные категории:
1.Сортировки прямым включением Bу insertion .
2.Сортировки прямым выделением Bу selection .
3.Сортировки прямым обменом Bу exchange .
К прямым методам относится метод прямого выбора.
Рассматриваем весь ряд массива и выбираем элемент меньший или больший элемента а(i), определяем его место в массиве - k, и затем меняем местами элемент а(i) и элемент а(k).
for i = 1 to n - 1
x = a(i)
k = i
for j = i + 1 to n
if x > a(j) then
k = j
x = a(k)
endif
next j
a(k) = a(i)
a(i) = x
next i
return
for i := 1 to n - 1 do
begin
x := a[i];
k := i;
for j := i + 1 to n do
if x > a[j] then
begin
k := j;
x := a[k];
end;
a[k] := a[i];
a[i] := x;
end;
Эффективность алгоритма:
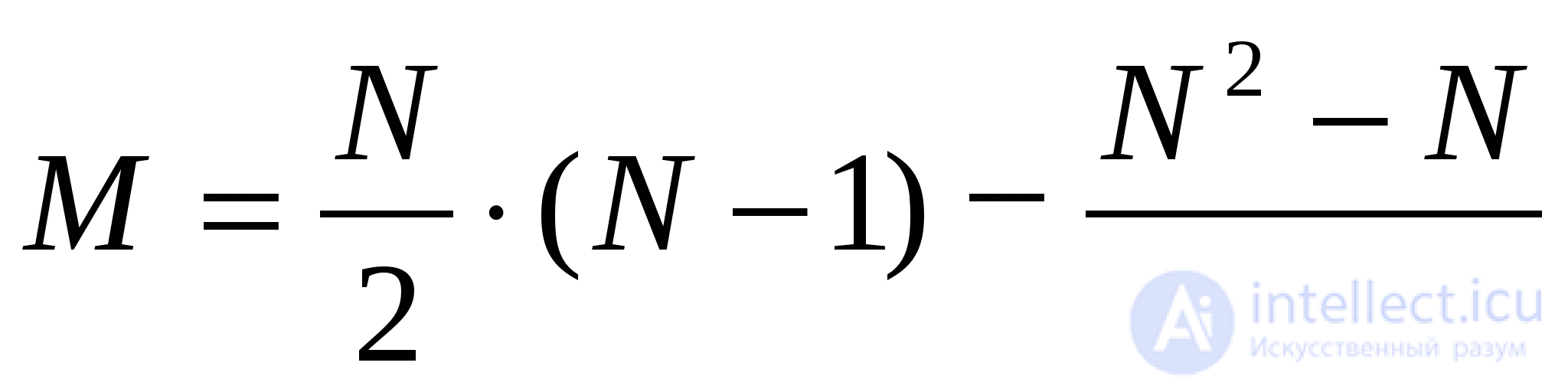
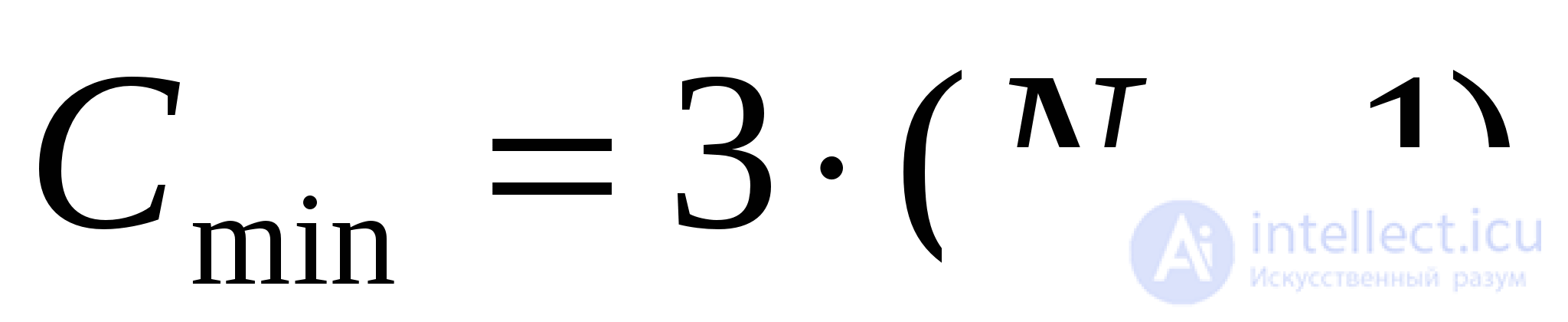

В худшем случае сортировка прямым выбором дает порядок n2, как и для числа сравнений, так и для числа перемещений.
Создать группу из N студентов. Ввести их: фамилия, имя, год рождения, оценки по предметам: стр. и алг.данных, высш. математика, физика, программирование, общий балл сдачи сессии; Разработать программу с использованием метода "прямого выбора", которая бы осуществляла сортировку (согласно варианту) :
1. Фамилий студентов по алфавиту.
2. Фамилий студентов по алфавиту в обратном порядке.
3. Студентов по старшинству (начиная со старшего).
4. Студентов по старшинству (начиная с младшего).
5. Студентов по общему баллу (по возрастанию).
6. Студентов по общему баллу (по убыванию).
7. Студентов по результатам 1-го экзамена (по возрастанию).
8. Студентов по результатам 2-го экзамена (по убыванию).
9. Студентов по результатам 3-го экзамена (по возрастанию).
10. Студентов по результатам 4-го экзамена (по убыванию).
11. Имен в алфавитном порядке.
12. Имен в обратном алфавитном порядке.
На этом все! Теперь вы знаете все про сортировка методом прямого выбора, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое сортировка методом прямого выбора, сортировка и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Из статьи мы узнали кратко, но содержательно про сортировка методом прямого выбора
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных