Лекция
Сразу хочу сказать, что здесь никакой воды про деревья поиска, и только нужная информация. Для того чтобы лучше понимать что такое деревья поиска, авл-дерево сплей-дерево, декартово дерево , настоятельно рекомендую прочитать все из категории Структуры данных.
бывают следующих видов
2-3 дерево
B-дерево
Fusion tree
Rope
Splay-дерево
Tango-дерево
АВЛ-дерево
декартово дерево
Декартово дерево по неявному ключу
Дерево ван Эмде Боаса
Дерево поиска, наивная реализация
Красно-черное дерево
Обзор поисковых структур данных
Поисковые структуры данных
Рандомизированное бинарное дерево поиска
Сверхбыстрый цифровой бор
Упорядоченное множество
АВЛ-дерево — сбалансированное по высоте двоичное дерево поиска: для каждой его вершины высота ее двух поддеревьев различается не более чем на 1.
АВЛ — аббревиатура, образованная первыми буквами создателей (советских ученых) Адельсон-Вельского Георгия Максимовича и Ландиса Евгения Михайловича.
Везде утверждается, что АВЛ-деревья проще красно-черных деревьев, но глядя на прилагаемый к этому код, начинаешь сомневаться в данном утверждении. Собственно, желание объяснить на пальцах, как устроены АВЛ-деревья, и послужило мотивацией к написанию данного поста. Изложение иллюстрируется кодом на С++.
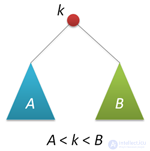 АВЛ-дерево — это прежде всего двоичное дерево поиска, ключи которого удовлетворяют стандартному свойству: ключ любого узла дерева не меньше любого ключа в левом поддереве данного узла и не больше любого ключа в правом поддереве этого узла. Это значит, что для поиска нужного ключа в АВЛ-дереве можно использовать стандартный алгоритм. Для простоты дальнейшего изложения будем считать, что все ключи в дереве целочисленны и не повторяются.
АВЛ-дерево — это прежде всего двоичное дерево поиска, ключи которого удовлетворяют стандартному свойству: ключ любого узла дерева не меньше любого ключа в левом поддереве данного узла и не больше любого ключа в правом поддереве этого узла. Это значит, что для поиска нужного ключа в АВЛ-дереве можно использовать стандартный алгоритм. Для простоты дальнейшего изложения будем считать, что все ключи в дереве целочисленны и не повторяются.
Особенностью АВЛ-дерева является то, что оно является сбалансированным в следующем смысле:для любого узла дерева высота его правого поддерева отличается от высоты левого поддерева не более чем на единицу. Доказано, что этого свойства достаточно для того, чтобы высота дерева логарифмически зависела от числа его узлов: высота h АВЛ-дерева с n ключами лежит в диапазоне от log2(n + 1) до 1.44 log2(n + 2) − 0.328. А так как основные операции над двоичными деревьями поиска (поиск, вставка и удаление узлов) линейно зависят от его высоты, то получаем гарантированную логарифмическую зависимость времени работы этих алгоритмов от числа ключей, хранимых в дереве. Напомним, что рандомизированные деревья поиска обеспечивают сбалансированность только в вероятностном смысле: вероятность получения сильно несбалансированного дерева при больших n хотя и является пренебрежимо малой, но остается не равной нулю.
Будем представлять узлы АВЛ-дерева следующей структурой:
struct node // структура для представления узлов дерева
{
int key;
unsigned char height;
node* left;
node* right;
node(int k) { key = k; left = right = 0; height = 1; }
};
Поле key хранит ключ узла, поле height — высоту поддерева с корнем в данном узле, поля left и right — указатели на левое и правое поддеревья. Простой конструктор создает новый узел (высоты 1) с заданным ключом k.
Традиционно, узлы АВЛ-дерева хранят не высоту, а разницу высот правого и левого поддеревьев (так называемый balance factor), которая может принимать только три значения -1, 0 и 1. Однако, заметим, что эта разница все равно хранится в переменной, размер которой равен минимум одному байту (если не придумывать каких-то хитрых схем «эффективной» упаковки таких величин). Вспомним, что высота h < 1.44 log2(n + 2), это значит, например, что при n=109 (один миллиард ключей, больше 10 гигабайт памяти под хранение узлов) высота дерева не превысит величины h=44, которая с успехом помещается в тот же один байт памяти, что и balance factor. Таким образом, хранение высот с одной стороны не увеличивает объем памяти, отводимой под узлы дерева, а с другой стороны существенно упрощает реализацию некоторых операций.
Определим три вспомогательные функции, связанные с высотой. Первая является оберткой для поля height, она может работать и с нулевыми указателями (с пустыми деревьями):
unsigned char height(node* p)
{
return p?p->height:0;
}
Вторая вычисляет balance factor заданного узла (и работает только с ненулевыми указателями):
int bfactor(node* p)
{
return height(p->right)-height(p->left);
}
Третья функция восстанавливает корректное значение поля height заданного узла (при условии, что значения этого поля в правом и левом дочерних узлах являются корректными):
void fixheight(node* p)
{
unsigned char hl = height(p->left);
unsigned char hr = height(p->right);
p->height = (hl>hr?hl:hr)+1;
}
Заметим, что все три функции являются нерекурсивными, т.е. время их работы есть величина О(1).
Максимальная высота АВЛ-дерева при заданном числе узлов :
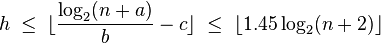
где:
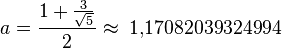 (округлить вверх),
(округлить вверх),
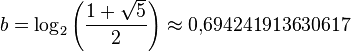 (округлить вниз),
(округлить вниз),
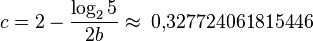 (округлить вниз).
(округлить вниз).
Стоит отметить, что количество возможных высот на практике сильно ограничено (при 32-битной адресации максимальная высота равна 45, при 48-битной — 68), поэтому лучше, возможно, заранее подсчитать все значения минимального количества узлов для каждой высоты с помощью рекуррентной формулы для дерева Фибоначчи:
 ,
,
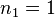 ,
,
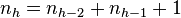 .
.
Промежуточные значения количества узлов будут соответствовать предыдущей (меньшей) высоте.
В процессе добавления или удаления узлов в АВЛ-дереве возможно возникновение ситуации, когда balance factor некоторых узлов оказывается равными 2 или -2, т.е. возникает расбалансировка поддерева. Для выправления ситуации применяются хорошо нам известные повороты вокруг тех или иных узлов дерева. Напомню, что простой поворот вправо (влево) производит следующую трансформацию дерева:
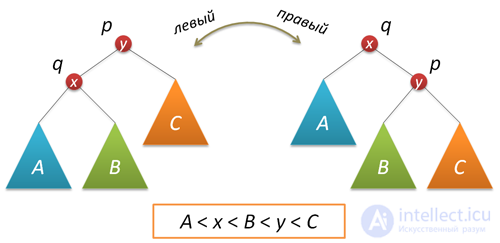
Код, реализующий правый поворот, выглядит следующим образом (как обычно, каждая функция, изменяющая дерево, возвращает новый корень полученного дерева):
node* rotateright(node* p) // правый поворот вокруг p
{
node* q = p->left;
p->left = q->right;
q->right = p;
fixheight(p);
fixheight(q);
return q;
}
Левый поворот является симметричной копией правого:
node* rotateleft(node* q) // левый поворот вокруг q
{
node* p = q->right;
q->right = p->left;
p->left = q;
fixheight(q);
fixheight(p);
return p;
}
Рассмотрим теперь ситуацию дисбаланса, когда высота правого поддерева узла p на 2 больше высоты левого поддерева (обратный случай является симметричным и реализуется аналогично). Пусть q — правый дочерний узел узла p, а s — левый дочерний узел узла q.

Анализ возможных случаев в рамках данной ситуации показывает, что для исправления расбалансировки в узле p достаточно выполнить либо простой поворот влево вокруг p, либо так называемый большой поворот влево вокруг того же p. Простой поворот выполняется при условии, что высота левого поддерева узла q больше высоты его правого поддерева: h(s)≤h(D).
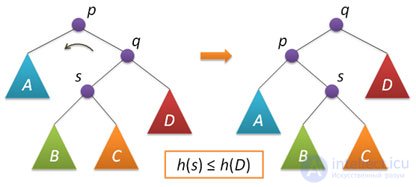
Большой поворот применяется при условии h(s)>h(D) и сводится в данном случае к двум простым — сначала правый поворот вокруг q и затем левый вокруг p.

Код, выполняющий балансировку, сводится к проверке условий и выполнению поворотов:
node* balance(node* p) // балансировка узла p
{
fixheight(p);
if( bfactor(p)==2 )
{
if( bfactor(p->right) < 0 )
p->right = rotateright(p->right);
return rotateleft(p);
}
if( bfactor(p)==-2 )
{
if( bfactor(p->left) > 0 )
p->left = rotateleft(p->left);
return rotateright(p);
}
return p; // балансировка не нужна
}
Описанные функции поворотов и балансировки также не содержат ни циклов, ни рекурсии, а значит выполняются за постоянное время, не зависящее от размера АВЛ-дерева.
Относительно АВЛ-дерева балансировкой вершины называется операция, которая в случае разницы высот левого и правого поддеревьев = 2, изменяет связи предок-потомок в поддереве данной вершины так, что разница становится <= 1, иначе ничего не меняет. Указанный результат получается вращениями поддерева данной вершины.
Используются 4 типа вращений:
1.Малое левое вращение 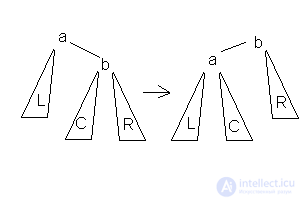 Данное вращение используется тогда, когда высота b-поддерева — высота L = 2 и высота С <= высота R.
Данное вращение используется тогда, когда высота b-поддерева — высота L = 2 и высота С <= высота R.
2.Большое левое вращение 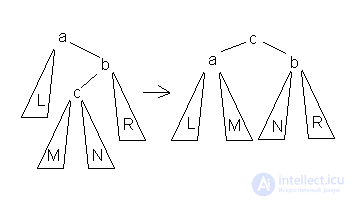 Данное вращение используется тогда, когда высота b-поддерева — высота L = 2 и высота c-поддерева > высота R.
Данное вращение используется тогда, когда высота b-поддерева — высота L = 2 и высота c-поддерева > высота R.
3.Малое правое вращение 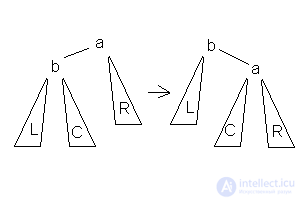 Данное вращение используется тогда, когда высота b-поддерева — высота R = 2 и высота С <= высота L.
Данное вращение используется тогда, когда высота b-поддерева — высота R = 2 и высота С <= высота L.
4.Большое правое вращение 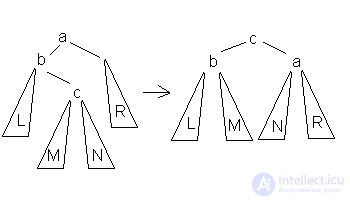 Данное вращение используется тогда, когда высота b-поддерева — высота R = 2 и высота c-поддерева > высота L.
Данное вращение используется тогда, когда высота b-поддерева — высота R = 2 и высота c-поддерева > высота L.
В каждом случае достаточно просто доказать то, что операция приводит к нужному результату и что полная высота уменьшается не более чем на 1 и не может увеличиться. Также можно заметить, что большое вращение это комбинация правого и левого малого вращения. Из-за условия балансированности высота дерева О(log(N)), где N- количество вершин, поэтому добавление элемента требует O(log(N)) операций.
Вставка нового ключа в АВЛ-дерево выполняется, по большому счету, так же, как это делается в простых деревьях поиска: спускаемся вниз по дереву, выбирая правое или левое направление движения в зависимости от результата сравнения ключа в текущем узле и вставляемого ключа. Единственное отличие заключается в том, что при возвращении из рекурсии (т.е. после того, как ключ вставлен либо в правое, либо в левое поддерево, и это дерево сбалансировано) выполняется балансировка текущего узла. Строго доказывается, что возникающий при такой вставке дисбаланс в любом узле по пути движения не превышает двух, а значит применение вышеописанной функции балансировки является корректным.
node* insert(node* p, int k) // вставка ключа k в дерево с корнем p
{
if( !p ) return new node(k);
if( kkey )
p->left = insert(p->left,k);
else
p->right = insert(p->right,k);
return balance(p);
}
Чтобы проверить соответствие реализованного алгоритма вставки теоретическим оценкам для высоты АВЛ-деревьев, был проведен несложный вычислительный эксперимент. Генерировался массив из случайно расположенных чисел от 1 до 10000, далее эти числа последовательно вставлялись в изначально пустое АВЛ-дерево и измерялась высота дерева после каждой вставки. Полученные результаты были усреднены по 1000 расчетам. На следующем графике показана зависимость от n средней высоты (красная линия); минимальной высоты (зеленая линия); максимальной высоты (синяя линия). Кроме того, показаны верхняя и нижняя теоретические оценки.
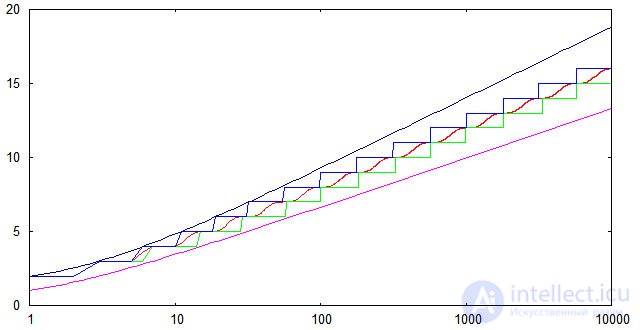
Видно, что для случайных последовательностей ключей экспериментально найденные высоты попадают в теоретические границы даже с небольшим запасом. Нижняя граница достижима (по крайней мере в некоторых точках), если исходная последовательность ключей является упорядоченной по возрастанию.
Показатель сбалансированности в дальнейшем будем интерпретировать как разность между высотой левого и правого поддерева, а алгоритм будет основаться на типе TAVLTree, описанном выше. Непосредственно при вставке (листу) присваивается нулевой баланс. Процесс включения вершины состоит из трех частей (данный процесс описан Никлаусом Виртом в «Алгоритмы и структуры данных»):
Будем возвращать в качестве результата функции, уменьшилась высота дерева или нет. Предположим, что процесс из левой ветви возвращается к родителю (рекурсия идет назад), тогда возможны три случая: { hl — высота левого поддерева, hr — высота правого поддерева } Включение вершины в левое поддерево приведет к
В третьей ситуации требуется определить балансировку левого поддерева. Если левое поддерево этой вершины (Tree^.left^.left) выше правого (Tree^.left^.right), то требуется большое правое вращение, иначе хватит малого правого. Аналогичные (симметричные) рассуждения можно привести и для включение в правое поддерево.
С удалением узлов из АВЛ-дерева, к сожалению, все не так шоколадно, как с рандомизированными деревьями поиска. Способа, основанного на слиянии (join) двух деревьев, ни найти, ни придумать не удалось. 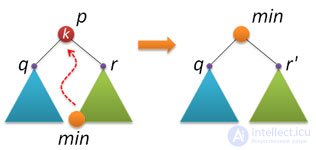 Поэтому за основу был взят вариант, описываемый практически везде (и который обычно применяется и при удалении узлов из стандартного двоичного дерева поиска). Идея следующая: находим узел p с заданным ключом k (если не находим, то делать ничего не надо), в правом поддереве находим узел min с наименьшим ключом и заменяем удаляемый узел p на найденный узел min.
Поэтому за основу был взят вариант, описываемый практически везде (и который обычно применяется и при удалении узлов из стандартного двоичного дерева поиска). Идея следующая: находим узел p с заданным ключом k (если не находим, то делать ничего не надо), в правом поддереве находим узел min с наименьшим ключом и заменяем удаляемый узел p на найденный узел min.
При реализации возникает несколько нюансов. Прежде всего, если у найденный узел p не имеет правого поддерева, то по свойству АВЛ-дерева слева у этого узла может быть только один единственный дочерний узел (дерево высоты 1), либо узел p вообще лист. В обоих этих случаях надо просто удалить узел p и вернуть в качестве результата указатель на левый дочерний узел узла p.
Пусть теперь правое поддерево у p есть. Находим минимальный ключ в этом поддереве. По свойству двоичного дерева поиска этот ключ находится в конце левой ветки, начиная от корня дерева. Применяем рекурсивную функцию:
node* findmin(node* p) // поиск узла с минимальным ключом в дереве p
{
return p->left?findmin(p->left):p;
}
Еще одна служебная функция у нас будет заниматься удалением минимального элемента из заданного дерева. Опять же, по свойству АВЛ-дерева у минимального элемента справа либо подвешен единственный узел, либо там пусто. В обоих случаях надо просто вернуть указатель на правый узел и по пути назад (при возвращении из рекурсии) выполнить балансировку. Сам минимальный узел не удаляется, т.к. он нам еще пригодится.
node* removemin(node* p) // удаление узла с минимальным ключом из дерева p
{
if( p->left==0 )
return p->right;
p->left = removemin(p->left);
return balance(p);
}
Теперь все готово для реализации удаления ключа из АВЛ-дерева. Сначала находим нужный узел, выполняя те же действия, что и при вставке ключа:
node* remove(node* p, int k) // удаление ключа k из дерева p
{
if( !p ) return 0;
if( k < p->key )
p->left = remove(p->left,k);
else if( k > p->key )
p->right = remove(p->right,k);
Как только ключ k найден, переходим к плану Б: запоминаем корни q и r левого и правого поддеревьев узла p; удаляем узел p; если правое поддерево пустое, то возвращаем указатель на левое поддерево; если правое поддерево не пустое, то находим там минимальный элемент min, потом его извлекаем оттуда, слева к min подвешиваем q, справа — то, что получилось из r, возвращаем min после его балансировки.
else // k == p->key
{
node* q = p->left;
node* r = p->right;
delete p;
if( !r ) return q;
node* min = findmin(r);
min->right = removemin(r);
min->left = q;
return balance(min);
}
При выходе из рекурсии не забываем выполнить балансировку:
return balance(p); }
Вот собственно и все! Поиск минимального узла и его извлечение, в принципе, можно реализовать в одной функции, при этом придется решать (не очень сложную) проблему с возвращением из функции пары указателей. Зато можно сэкономить на одном проходе по правому поддереву.
Очевидно, что операции вставки и удаления (а также более простая операция поиска) выполняются за время пропорциональное высоте дерева, т.к. в процессе выполнения этих операций производится спуск из корня к заданному узлу, и на каждом уровне выполняется некоторое фиксированное число действий. А в силу того, что АВЛ-дерево является сбалансированным, его высота зависит логарифмически от числа узлов. Таким образом, время выполнения всех трех базовых операций гарантированно логарифмически зависит от числа узлов дерева.
Для простоты опишем рекурсивный алгоритм удаления. Если вершина — лист, то удалим ее и вызовем балансировку всех ее предков в порядке от родителя к корню. Иначе найдем самую близкую по значению вершину в поддереве наибольшей высоты (правом или левом) и переместим ее на место удаляемой вершины, при этом вызвав процедуру ее удаления.
Докажем, что данный алгоритм сохраняет балансировку. Для этого докажем по индукции по высоте дерева, что после удаления некоторой вершины из дерева и последующей балансировки высота дерева уменьшается не более, чем на 1. База индукции: Для листа очевидно верно. Шаг индукции: Либо условие балансированности в корне (после удаления корень может изменится) не нарушилось, тогда высота данного дерева не изменилась, либо уменьшилось строго меньшее из поддеревьев => высота до балансировки не изменилась => после уменьшится не более чем на 1.
Очевидно, что в результате указанных действий процедура удаления вызывается не более 3 раз, так как у вершины, удаляемой по второму вызову, нет одного из поддеревьев. Но поиск ближайшего каждый раз требует O(N) операций. Становится очевидной возможность оптимизации: поиск ближайшей вершины может быть выполнен по краю поддерева, что сокращает сложность до O(log(N)).
Нерекурсивный алгоритм сложнее рекурсивного.
Для реализации удаления будем исходить из того же принципа, что и при вставке: найдем вершину, удаление из которой не приведет к изменению ее высоты. Существует два случая:
Для облегчения понимания приведенный алгоритм не содержит каких-либо оптимизаций. В отличие от рекурсивного алгоритма, найденная удаляемая вершина заменяется значением из левой подветви. Этот алгоритм можно оптимизировать так же, как и рекурсивный (за счет того, что после нахождения удаляемой вершины известно направление движения):
Как уже говорилось, если удаляемая вершина — лист, то она удаляется, и обратный обход дерева происходит от родителя удаленного листа. Если не лист — ей находится «замена», и обратный обход дерева происходит от родителя «замены». Непосредственно после удаления элемента — «замена» получает баланс удаляемого узла.
При обратном обходе: если при переходе к родителю пришли слева — баланс увеличивается на 1, если же пришли справа — уменьшается на 1.
Это делается до тех пор, пока при изменении баланса он не станет равным −1 или 1 (обратите внимание на различие с вставкой элемента!): в данном случае такое изменение баланса будет гласить о неизменной дельта-высоте поддеревьев. Повороты происходят по тем же правилам, что и при вставке.
Обозначим:
Если поворот осуществляется при вставке элемента, то баланс Pivot’а равен либо 1, либо −1. В таком случае после поворота балансы обоих устанавливаются равными 0. При удалении все иначе: баланс Pivot’а может стать равным 0 (в этом легко убедиться).
Приведем сводную таблицу зависимости финальных балансов от направления поворота и исходного баланса узла Pivot:
| Направление поворота | Old Pivot.Balance | New Current.Balance | New Pivot.Balance |
|---|---|---|---|
| Левый или Правый | -1 или +1 | 0 | 0 |
| Правый | 0 | -1 | +1 |
| Левый | 0 | +1 | -1 |
Pivot и Current — те же самые, но добавляется третий участник поворота. Обозначим его за «Bottom»: это (при двойном правом повороте) левый сын Pivot’а, а при двойном левом — правый сын Pivot’а.
При данном повороте — Bottom в результате всегда приобретает баланс 0, но от его исходного баланса зависит расстановка балансов для Pivot и Current.
Приведем сводную таблицу зависимости финальных балансов от направления поворота и исходного баланса узла Bottom:
| Направление | Old Bottom.Balance | New Current.Balance | New Pivot.Balance |
|---|---|---|---|
| Левый или Правый | 0 | 0 | 0 |
| Правый | +1 | 0 | -1 |
| Правый | -1 | +1 | 0 |
| Левый | +1 | -1 | 0 |
| Левый | -1 | 0 | +1 |
Из формулы, приведенной выше, высота АВЛ-дерева никогда не превысит высоту идеально сбалансированного дерева более, чем на 45%. Для больших 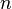 имеет место оценка
имеет место оценка 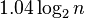 . Таким образом, выполнение основных операций требует порядка
. Таким образом, выполнение основных операций требует порядка  сравнений. Экспериментально выяснено, что одна балансировка приходится на каждые 2 включения и на каждые 5 исключений.
сравнений. Экспериментально выяснено, что одна балансировка приходится на каждые 2 включения и на каждые 5 исключений.
Расширяющееся (англ. splay tree) или косое дерево является двоичным деревом поиска, в котором поддерживается свойство сбалансированности. Это дерево принадлежит классу «саморегулирующихся деревьев», которые поддерживают необходимый баланс ветвления дерева, чтобы обеспечить выполнение операций поиска, добавления и удаления за логарифмическое время от числа хранимых элементов. Об этом говорит сайт https://intellect.icu . Это реализуется без использования каких-либо дополнительных полей в узлах дерева (как, например, в Красно-черных деревьях или АВЛ-деревьях, где в вершинах хранится, соответственно, цвет вершины и глубина поддерева). Вместо этого «расширяющие операции» (splay operation), частью которых являются вращения, выполняются при каждом обращении к дереву. Учетная стоимость (англ.) в расчете на одну операцию с деревом составляет 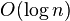 .
.
Расширяющееся дерево придумали Роберт Тарьян и Даниель Слейтор в 1983 г.
Сплей-дерево (англ. Splay-tree) — это двоичное дерево поиска. Оно позволяет находить быстрее те данные, которые использовались недавно. Относится к разряду сливаемых деревьев. Сплей-дерево было придумано Робертом Тарьяном и Даниелем Слейтером в 1983 году.
Для того, чтобы доступ к недавно найденным данным был быстрее, надо, чтобы эти данные находились ближе к корню. Этого мы можем добиться, используя различные эвристики:
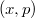 , где
, где  — найденная вершина,
— найденная вершина, 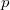 — ее предок, пока
— ее предок, пока  не окажется корнем дерева. Однако можно построить такую последовательность операций, что амортизированное время доступа к вершине будет
не окажется корнем дерева. Однако можно построить такую последовательность операций, что амортизированное время доступа к вершине будет 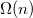 .
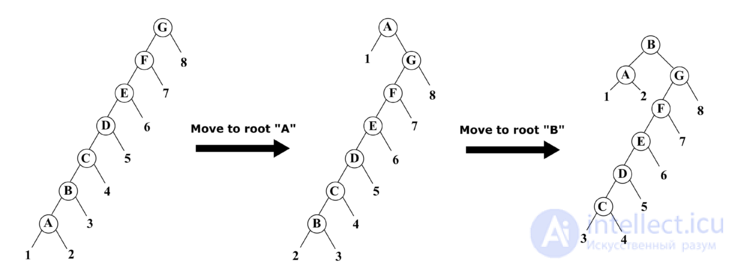
.Пример: При последовательном использовании операций "move to root" для вершин 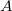 и
и 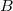 требуется по 6 поворотов, в то время как при использовании операции "splay" для вершины
требуется по 6 поворотов, в то время как при использовании операции "splay" для вершины 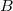 достаточно 3 поворотов.
достаточно 3 поворотов.

"splay" делится на 3 случая:
zig
Если 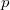 — корень дерева с сыном
— корень дерева с сыном  , то совершаем один поворот вокруг ребра
, то совершаем один поворот вокруг ребра 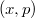 , делая
, делая  корнем дерева. Данный случай является крайним и выполняется только один раз в конце, если изначальная глубина
корнем дерева. Данный случай является крайним и выполняется только один раз в конце, если изначальная глубина  была нечетной.
была нечетной.
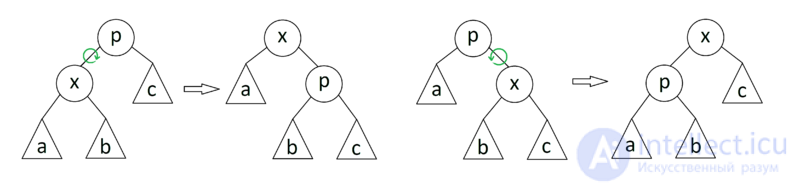
zig-zig
Если 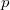 — не корень дерева, а
— не корень дерева, а  и
и 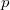 — оба левые или оба правые дети, то делаем поворот ребра
— оба левые или оба правые дети, то делаем поворот ребра 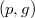 , где
, где 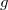 отец
отец 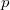 , а затем поворот ребра
, а затем поворот ребра 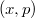 .
.
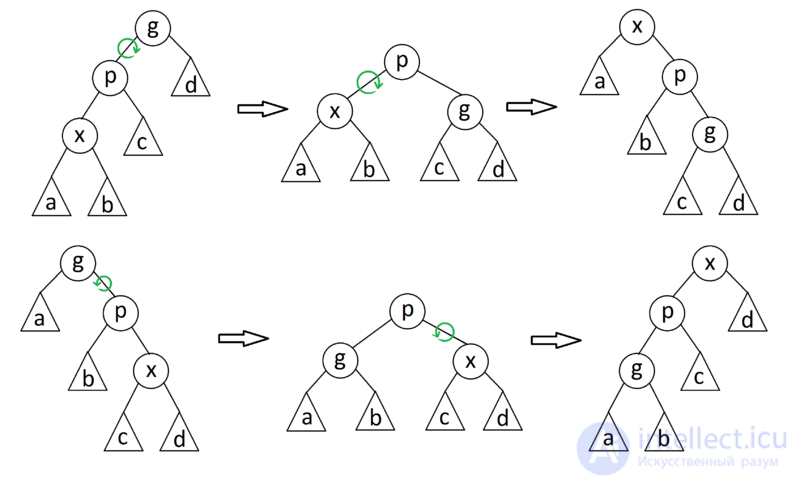
zig-zag
Если 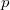 — не корень дерева и
— не корень дерева и  — левый ребенок, а
— левый ребенок, а 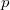 — правый, или наоборот, то делаем поворот вокруг ребра
— правый, или наоборот, то делаем поворот вокруг ребра 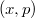 , а затем поворот нового ребра
, а затем поворот нового ребра 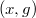 , где
, где 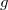 — бывший родитель
— бывший родитель 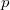 .
.
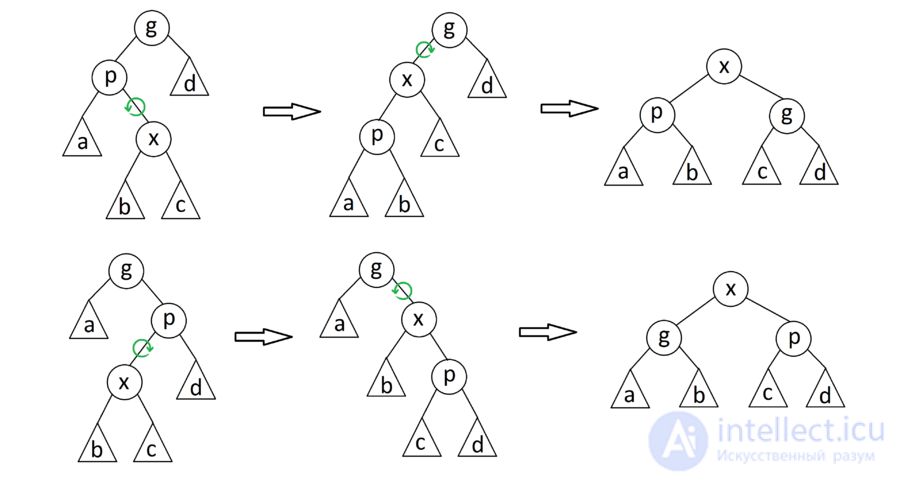
Данная операция занимает 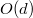 времени, где
времени, где  — длина пути от
— длина пути от  до корня.
до корня.
Эта операция выполняется как для обычного бинарного дерева, только после нее запускается операция splay.
У нас есть два дерева  и
и 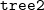 , причем подразумевается, что все элементы первого дерева меньше элементов второго. Запускаем splay от самого большого элемента в дереве
, причем подразумевается, что все элементы первого дерева меньше элементов второго. Запускаем splay от самого большого элемента в дереве  (пусть это элемент
(пусть это элемент 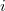 ). После этого корень
). После этого корень  содержит элемент
содержит элемент 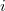 , при этом у него нет правого ребенка. Делаем
, при этом у него нет правого ребенка. Делаем 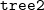 правым поддеревом
правым поддеревом 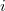 и возвращаем полученное дерево.
и возвращаем полученное дерево.
Запускаем splay от элемента  и возвращаем два дерева, полученные отсечением правого или левого поддерева от корня, в зависимости от того, содержит корень элемент больше или не больше, чем
и возвращаем два дерева, полученные отсечением правого или левого поддерева от корня, в зависимости от того, содержит корень элемент больше или не больше, чем  .
.
Запускаем split(tree, x), который нам возвращает деревья  и
и 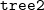 , их подвешиваем к
, их подвешиваем к  как левое и правое поддеревья соответственно.
как левое и правое поддеревья соответственно.
Запускаем splay от  элемента и возвращаем Merge от его детей.
элемента и возвращаем Merge от его детей.
Амортизационный анализ сплей-дерева проводится с помощью метода потенциалов. Потенциалом рассматриваемого дерева назовем сумму рангов его вершин. Ранг вершины  — это величина, обозначаемая
— это величина, обозначаемая 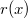 и равная
и равная 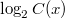 , где
, где  — количество вершин в поддереве с корнем в
— количество вершин в поддереве с корнем в  .
.
| Лемма: |
Амортизированное время операции splay вершины  в дереве с корнем в дереве с корнем  не превосходит не превосходит 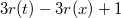 |
| Доказательство: |
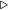 |
|
Проанализируем каждый шаг операции splay. Пусть Разберем случаи в зависимости от типа шага: zig. Поскольку выполнен один поворот, то амортизированное время выполнения шага zig-zig. Выполнено два поворота, амортизированное время выполнения шага Далее, так как Мы утверждаем, что эта сумма не превосходит Из рисунка видно, что zig-zag. Выполнено два поворота, амортизированное время выполнения шага Мы утверждаем, что эта сумма не превосходит Итого, получаем, что амортизированное время шага zig-zag не превосходит 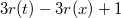 , поскольку утроенные ранги промежуточных вершин сокращаются (входят в сумму как с плюсом, так и с минусом). Тогда суммарное время работы splay , поскольку утроенные ранги промежуточных вершин сокращаются (входят в сумму как с плюсом, так и с минусом). Тогда суммарное время работы splay 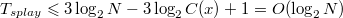 , где , где 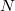 — число элементов в дереве. — число элементов в дереве. |
 |
| Теорема: |
|
Если к ключам |
| Доказательство: |
 |
|
Известно, что Пусть Обозначим за Пусть  — корень — корень 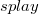 -дерева, то очевидно, что -дерева, то очевидно, что  , следовательно , следовательно  . Поэтому . Поэтому 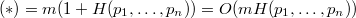 , ч.т.д. , ч.т.д. |
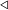 |
| Теорема (о близких запросах в сплей-дереве): |
|
Пусть в сплей-дерево сложены ключи |
| Доказательство: |
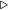 |
|
Для доказательства теоремы воспользуемся методом потенциалов:
По условию выполняется
Введем следующие обозначения:
Пусть Последнее верно, так как при фиксированном Из определения размера узла следует, что Также заметим, что для любого Тогда, воспользовавшись полученными оценками, найдем изменение потенциала сплей-дерева после
Первое неравенство верно, так как максимальное значение потенциала достигается при Обозначим за
Докажем, что данное определение потенциала удовлетворяет условию теоремы о методе потенциалов. Для любого Тогда, подставляя найденные значения в формулу   . . |
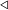 |
Данная теорема показывает, что сплей-деревья поддерживают достаточно эффективный доступ к ключам, которые находятся близко к какому-то фиксированному ключу.
Splay-дерево по неявному ключу полностью аналогично декартову дереву по неявному ключу, неявным ключом также будет количество элементов дерева, меньших данного. Аналогично, будем хранить вспомогательную величину  — количество вершин в поддереве. К операциям, которые уже были представлены в декартовом дереве, добавляется splay, но пересчет
— количество вершин в поддереве. К операциям, которые уже были представлены в декартовом дереве, добавляется splay, но пересчет  в ней тривиален, так как мы точно знаем, куда перемещаются изменяемые поддеревья.
в ней тривиален, так как мы точно знаем, куда перемещаются изменяемые поддеревья.
Декартово дерево или дерамида (англ. Treap) — это структура данных, объединяющая в себе бинарное дерево поиска и бинарную кучу (отсюда и второе ее название: treap (tree + heap) и дерамида (дерево + пирамида), также существует название курево (куча + дерево).
Декартово дерево — это двоичное дерево, в узлах которого хранятся:
Ссылка на родительский узел не обязательна, она желательна только для линейного алгоритма построения дерева.
Декартово дерево не является самобалансирующимся в обычном смысле, и применяют его по следующим причинам:
Недостатки декартового дерева:
Более строго, это бинарное дерево, в узлах которого хранится пары 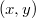 , где
, где  — это ключ, а
— это ключ, а  — это приоритет. Также оно является двоичным деревом поиска по
— это приоритет. Также оно является двоичным деревом поиска по  и пирамидой по
и пирамидой по  . Предполагая, что все
. Предполагая, что все  и все
и все  являются различными, получаем, что если некоторый элемент дерева содержит
являются различными, получаем, что если некоторый элемент дерева содержит 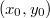 , то у всех элементов в левом поддереве
, то у всех элементов в левом поддереве  , у всех элементов в правом поддереве
, у всех элементов в правом поддереве 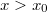 , а также и в левом, и в правом поддереве имеем:
, а также и в левом, и в правом поддереве имеем: 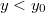 .
.
Дерамиды были предложены Сиделем (Siedel) и Арагоном (Aragon) в 1996 г.
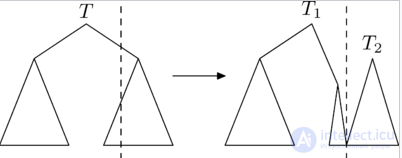
Операция split
Операция  (разрезать) позволяет сделать следующее, разрезать исходное дерево
(разрезать) позволяет сделать следующее, разрезать исходное дерево  по ключу
по ключу 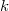 . Возвращать она будет такую пару деревьев
. Возвращать она будет такую пару деревьев 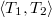 , что в дереве
, что в дереве 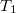 ключи меньше
ключи меньше 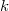 , а в дереве
, а в дереве 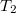 все остальные:
все остальные: .
.
Эта операция устроена следующим образом.
Рассмотрим случай, в котором требуется разрезать дерево по ключу, большему ключа корня. Посмотрим, как будут устроены результирующие деревья 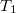 и
и 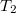 :
:
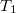 : левое поддерево
: левое поддерево 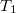 совпадет с левым поддеревом
совпадет с левым поддеревом  . Для нахождения правого поддерева
. Для нахождения правого поддерева 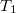 , нужно разрезать правое поддерево
, нужно разрезать правое поддерево  на
на  и
и 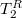 по ключу
по ключу 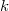 и взять
и взять  .
.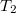 совпадет с
совпадет с 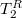 .
.Случай, в котором требуется разрезать дерево по ключу, меньше либо равному ключа в корне, рассматривается симметрично.
Treap, Treap
split(t: Treap, k: int): if t ==
return 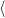
 ,
,
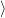
else if k > t.x
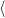 t1, t2
t1, t2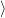 = split(t.right, k)
= split(t.right, k)
t.right = t1
return 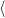 t, t2
t, t2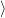
else
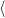 t1, t2
t1, t2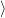 = split(t.left, k)
= split(t.left, k)
t.left = t2
return 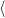 t1, t
t1, t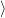
Оценим время работы операции  . Во время выполнения вызывается одна операция
. Во время выполнения вызывается одна операция  для дерева хотя бы на один меньшей высоты и делается еще
для дерева хотя бы на один меньшей высоты и делается еще 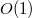 операций. Тогда итоговая трудоемкость этой операции равна
операций. Тогда итоговая трудоемкость этой операции равна 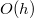 , где
, где 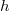 — высота дерева.
— высота дерева.
Операция merge
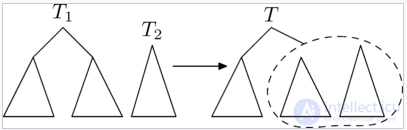
Рассмотрим вторую операцию с декартовыми деревьями —  (слить).
(слить).
С помощью этой операции можно слить два декартовых дерева в одно. Причем, все ключи в первом(левом) дереве должны быть меньше, чем ключи во втором(правом). В результате получается дерево, в котором есть все ключи из первого и второго деревьев: 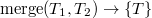
Рассмотрим принцип работы этой операции. Пусть нужно слить деревья 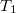 и
и 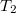 . Тогда, очевидно, у результирующего дерева
. Тогда, очевидно, у результирующего дерева  есть корень. Корнем станет вершина из
есть корень. Корнем станет вершина из 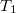 или
или 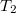 с наибольшим приоритетом
с наибольшим приоритетом  . Но вершина с самым большим
. Но вершина с самым большим  из всех вершин деревьев
из всех вершин деревьев 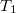 и
и 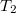 может быть только либо корнем
может быть только либо корнем 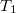 , либо корнем
, либо корнем 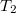 . Рассмотрим случай, в котором корень
. Рассмотрим случай, в котором корень 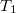 имеет больший
имеет больший  , чем корень
, чем корень 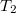 . Случай, в котором корень
. Случай, в котором корень 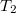 имеет больший
имеет больший  , чем корень
, чем корень 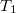 , симметричен этому.
, симметричен этому.
Если  корня
корня 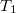 больше
больше  корня
корня 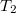 , то он и будет являться корнем. Тогда левое поддерево
, то он и будет являться корнем. Тогда левое поддерево  совпадет с левым поддеревом
совпадет с левым поддеревом 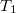 . Справа же нужно подвесить объединение правого поддерева
. Справа же нужно подвесить объединение правого поддерева 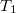 и дерева
и дерева 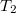 .
.
Treap merge(t1: Treap, t2: Treap): if t2 ==
return t1
if t1 ==
return t2
else if t1.y > t2.y
t1.right = merge(t1.right, t2)
return t1
else
t2.left = merge(t1, t2.left)
return t2
Рассуждая аналогично операции  приходим к выводу, что трудоемкость операции
приходим к выводу, что трудоемкость операции  равна
равна 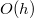 , где
, где 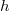 — высота дерева.
— высота дерева.
Операция 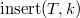 добавляет в дерево
добавляет в дерево  элемент
элемент 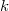 , где
, где 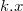 — ключ, а
— ключ, а 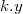 — приоритет.
— приоритет.
Представим что элемент 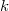 , это декартово дерево из одного элемента, и для того чтобы его добавить в наше декартово дерево
, это декартово дерево из одного элемента, и для того чтобы его добавить в наше декартово дерево  , очевидно, нам нужно их слить. Но
, очевидно, нам нужно их слить. Но  может содержать ключи как меньше, так и больше ключа
может содержать ключи как меньше, так и больше ключа 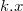 , поэтому сначала нужно разрезать
, поэтому сначала нужно разрезать  по ключу
по ключу 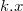 .
.
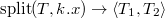 .
.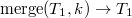 .
.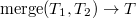 .
.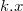 ), но останавливаемся на первом элементе, в котором значение приоритета оказалось меньше
), но останавливаемся на первом элементе, в котором значение приоритета оказалось меньше 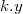 .
.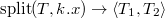 от найденного элемента (от элемента вместе со всем его поддеревом)
от найденного элемента (от элемента вместе со всем его поддеревом)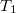 и
и 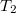 записываем в качестве левого и правого сына добавляемого элемента.
записываем в качестве левого и правого сына добавляемого элемента.В первой реализации два раза используется  , а во второй реализации слияние вообще не используется.
, а во второй реализации слияние вообще не используется.
Операция 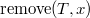 удаляет из дерева
удаляет из дерева  элемент с ключом
элемент с ключом  .
.
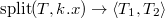 .
. , то есть самого левого ребенка дерева
, то есть самого левого ребенка дерева 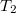 .
. .
. ), и ищем удаляемый элемент.
), и ищем удаляемый элемент. его левого и правого сыновей
его левого и правого сыновей ставим на место удаляемого элемента.
ставим на место удаляемого элемента.В первой реализации один раз используется  , а во второй реализации разрезание вообще не используется.
, а во второй реализации разрезание вообще не используется.
Пусть нам известно из каких пар 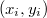 требуется построить декартово дерево, причем также известно, что
требуется построить декартово дерево, причем также известно, что 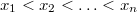 .
.
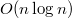
Отсортируем все приоритеты по убыванию за 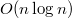 и выберем первый из них, пусть это будет
и выберем первый из них, пусть это будет 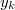 . Сделаем
. Сделаем 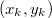 корнем дерева. Проделав то же самое с остальными вершинами получим левого и правого сына
корнем дерева. Проделав то же самое с остальными вершинами получим левого и правого сына 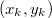 . В среднем высота Декартова дерева
. В среднем высота Декартова дерева 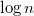 (см. далее) и на каждом уровне мы сделали
(см. далее) и на каждом уровне мы сделали 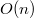 операций. Значит такой алгоритм работает за
операций. Значит такой алгоритм работает за 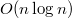 .
.
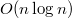
Отсортируем парочки 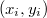 по убыванию
по убыванию  и положим их в очередь. Сперва достанем из очереди первый
и положим их в очередь. Сперва достанем из очереди первый 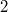 элемента и сольем их в дерево и положим в конец очереди, затем сделаем то же самое со следующими двумя и т.д. Таким образом, мы сольем сначала
элемента и сольем их в дерево и положим в конец очереди, затем сделаем то же самое со следующими двумя и т.д. Таким образом, мы сольем сначала  деревьев размера
деревьев размера  , затем
, затем 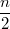 деревьев размера
деревьев размера 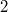 и так далее. При этом на уменьшение размера очереди в два раза мы будем тратить суммарно
и так далее. При этом на уменьшение размера очереди в два раза мы будем тратить суммарно 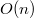 время на слияния, а всего таких уменьшений будет
время на слияния, а всего таких уменьшений будет 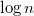 . Значит полное время работы алгоритма будет
. Значит полное время работы алгоритма будет 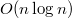 .
.
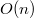
Будем строить дерево слева направо, то есть начиная с 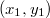 по
по 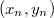 , при этом помнить последний добавленный элемент
, при этом помнить последний добавленный элемент 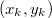 . Он будет самым правым, так как у него будет максимальный ключ, а по ключам декартово дерево представляет собой двоичное дерево поиска. При добавлении
. Он будет самым правым, так как у него будет максимальный ключ, а по ключам декартово дерево представляет собой двоичное дерево поиска. При добавлении  , пытаемся сделать его правым сыном
, пытаемся сделать его правым сыном 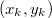 , это следует сделать если
, это следует сделать если  , иначе делаем шаг к предку последнего элемента и смотрим его значение
, иначе делаем шаг к предку последнего элемента и смотрим его значение  . Поднимаемся до тех пор, пока приоритет в рассматриваемом элементе меньше приоритета в добавляемом, после чего делаем
. Поднимаемся до тех пор, пока приоритет в рассматриваемом элементе меньше приоритета в добавляемом, после чего делаем  его правым сыном, а предыдущего правого сына делаем левым сыном
его правым сыном, а предыдущего правого сына делаем левым сыном  .
.
Заметим, что каждую вершину мы посетим максимум дважды: при непосредственном добавлении и, поднимаясь вверх (ведь после этого вершина будет лежать в чьем-то левом поддереве, а мы поднимаемся только по правому). Из этого следует, что построение происходит за 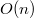 .
.
Мы уже выяснили, что сложность операций с декартовым деревом линейно зависит от его высоты. В действительности высота декартова дерева может быть линейной относительно его размеров. Например, высота декартова дерева, построенного по набору ключей 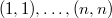 , будет равна
, будет равна  . Во избежание таких случаев, полезным оказывается выбирать приоритеты в ключах случайно.
. Во избежание таких случаев, полезным оказывается выбирать приоритеты в ключах случайно.
| Теорема: | ||||||
|
В декартовом дереве из |
||||||
| Доказательство: | ||||||
 |
||||||
|
Будем считать, что все выбранные приоритеты Для начала введем несколько обозначений:
В силу обозначений глубину вершины можно записать как количество предков:
Теперь можно выразить математическое ожидание глубины конкретной вершины:
Для подсчета средней глубины вершин нам нужно сосчитать вероятность того, что вершина Введем новое обозначение:
Так как распределение приоритетов равномерное, каждая вершина среди
Подставив последнее в нашу формулу с математическим ожиданием получим:
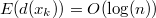 . . |
||||||
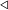 |
Таким образом, среднее время работы операций  и
и  будет
будет 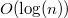 .
.
декартово дерево по неявному ключу ,
задачи rmq , задачи lca ,
А как ты думаешь, при улучшении деревья поиска, будет лучше нам? Надеюсь, что теперь ты понял что такое деревья поиска, авл-дерево сплей-дерево, декартово дерево и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных