Лекция
Привет, сегодня поговорим про статические структуры данных, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое статические структуры данных, полустатические структуры данных , настоятельно рекомендую прочитать все из категории Структуры данных.
Структуры данных - это совокупность элементов данных и отношений между ними. При этом под элементами данных может подразумеваться как простое данное так и структура данных. Под отношениями между данными понимают функциональные связи между ними и указатели на то, где находятся эти данные.
Графическое представление элемента структуры данных.

Элемент отношений - это совокупность всех связей элемента с другими элементами данных, рассматриваемой структуры.
S:=(D,R)
Где S - структура данных, D - данные и R - отношения.
Как бы сложна ни была структура данных, в конечном итоге она состоит из простых данных (см. рис. 2.2, 2.3).


Внутренний мир ЭВМ далеко не так прост, как мы думаем. Память машины состоит из миллионов триггеров, которые обрабатывают поступающую информацию
Мы, занося информацию в компьютер, представляем ее в каком-то виде, который на наш взгляд упорядочивает данные и придает им смысл. Машина отводит поле для поступающей информации и задает ей какой-то адрес. Таким образом получается, что мы обрабатываем данные на логическом уровне, как бы абстрактно, а машина делает это на физическом уровне.
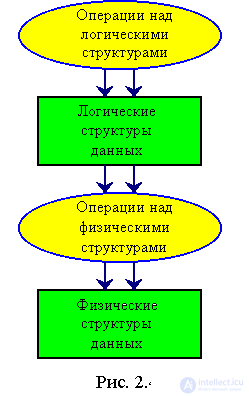
Последовательность переходов от логической организации к физической показана на рис. 2.4.
Структуры данных классифицируются:
1. По связанности данных в структуре:
- если данные в структуре связаны очень слабо, то такие структуры называются несвязанными (вектор, массив, строки, стеки)
- если данные в структуре связаны, то такие структуры называются связанными (связанные списки)
2. По изменчивости структуры во времени или в процессе выполнения программы:
- статические структуры - структуры, неменяющиеся до конца выполнения программы (записи, массивы, строки, вектора)
- полустатические структуры (стеки, деки, очереди)
- динамические структуры - происходит полное изменение при выполнении программы
3. По упорядоченности структуры:
- линейные (вектора, массивы, стеки, деки, записи)
- нелинейные (многосвязные списки, древовидные структуры, графы)
Наиболее важной характеристикой является изменчивость структуры во времени.
Самая простая статическая структура - это вектор. Вектор - это чисто линейная упорядоченная структура, где отношение между ее элементами есть строго выраженная последовательность элементов структуры (рис. 2.5).
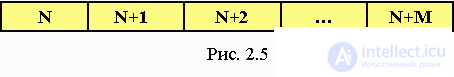
Каждый элемент вектора имеет свой индекс, определяющий положение данного элемента в векторе. Поскольку индексы являются целыми числами, над ними можно производить операции и, таким образом, вычислять положение элемента в структуре на логическом уровне доступа. Для доступа к элементу вектора, достаточно просто указать имя вектора (элемента) и его индекс .
Для доступа к этому элементу используется функция адресации, которая формирует из значения индекса адрес слота, где находится значение исходного элемента. Для объявления в программе вектора необходимо указать его имя, количество элементов и их тип (тип данных)
Пример:
var
M1: Array [1..100] of integer;
M2: Array [1..10] of real;
Вектор состоит из совершенно однотипных данных и количество их строго определено.
В общем случае элемент массива - это есть элемент вектора, который сам по себе тоже является элементом структуры (рис. 2.6).

Для доступа к элементу двумерного массива необходимы значения пары индексов (номер строки и номер столбца, на пересечении которых находится элемент). На физическом уровне двумерный массив выглядит также, как и одномерный (вектор), причем трансляторы представляют массивы либо в виде строк, либо в виде столбцов.
Запись представляет из себя структуру данных последовательного типа, где элементы структуры расположены один за другим как в логическом, так и в физическом представлении. Запись предполагает множество элементов разного типа. Элементы данных в записи часто называют полями записи.
Пример:
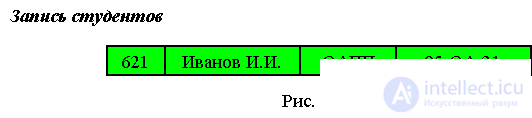
Логическая структура записи может быть представлена как в графическом виде, так и в табличном.


Элемент записи может включать в себя записи. В этом случае возникает сложная иерархическая структура данных.
Пример:
Необходимо заполнить запись о студенте, содержащую следующую информацию: N - порядковый номер студента; Имя студента, в составе которого должны быть: Фамилия, Имя, Отчество; Анкетные данные студента: год рождения, место рождения, родители: мать, отец; Факультет; Группа; Оценки, полученные в сессию: по английскому языку и микропроцессорам.
Ниже приведены два логических представления структуры этой записи.
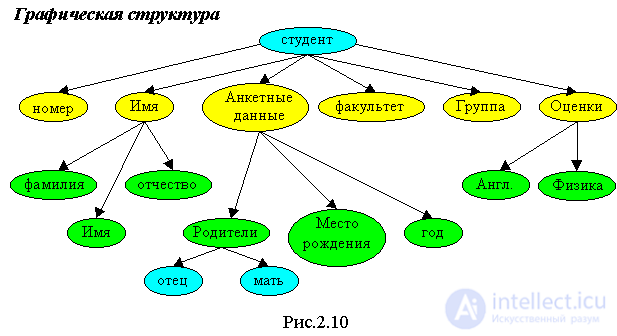
Получена четырехуровневая иерархическая структура данных. Информация содержится в листьях, остальные узлы служат для указания пути к листьям.
1-ый уровень Студент = запись
2-ой уровень Номер
2-ой уровень Имя = запись
3-ий уровень Фамилия
3-ий уровень Имя
3-ий уровень Отчество
2-ой уровень Анкетные данные = запись
3-ий уровень Место рождения
3-ий уровень Год рождения
3-ий уровень Родители = запись
4-ый уровень Мать
4-ый уровень Отец
2-ой уровень Факультет
2-ой уровень Группа
2-ой уровень Оценки = запись
3-ий уровень Английский
3-ий уровень Физика
Эта структура называется вложенной записью.
Операции над записями:
Таблица - это конечный набор записей (рис. 2.11).

При задании таблицы указывается количество содержащихся в ней записей.
Пример:
Type ST = Record
Num: Integer;
Name: String[15];
Fak: String ;
Group: String[10];
Angl: Integer;
Physic: Integer;
var
Table: Array [1..19] of St;
Элементом данных таблицы является запись. Об этом говорит сайт https://intellect.icu . Поэтому операции, которые производятся с таблицей - это операции, производимые с записью.
Операции с таблицами:
1. Поиск записи по заданному ключу.
2. Занесение новой записи в таблицу.
Ключ - это идентификатор записи. Для хранения этого идентификатора отводится специальное поле.
Составной ключ - ключ, содержащий более двух полей.
К полустатическим структурам данных относят стеки, деки и очереди.
Списки
Это набор связанных элементов данных, которые в общем случае могут быть разного типа.
Пример списка:
E1, E2, ........, En,... n > 1 и не зафиксировано.
Количество элементов списка может меняться в процессе выполнения программы. Различают 2 вида списков:
В несвязных списках связь между элементами данных выражена неявно. В связных списках в элемент данных заносится указатель связи с последующим или предыдущим элементом списка.
Стеки, деки и очереди - это несвязные списки. Кроме того они относятся к последовательным спискам, в которых неявная связь отображается их последовательностью.
Очередь вида LIFO (Last In First Out - Последним пришел, первым ушел ), при которой на обслуживание первым выбирается тот элемент очереди, который поступил в нее последним, называется стеком. Это одна из наиболее употребляемых структур данных, которая оказывается весьма удобной при решении различных задач.
В силу указанной дисциплины обслуживания, в стеке доступна единственая его позиция, которая называется вершиной стека- это позиция, в которой находится последний по времени поступления в стек элемент. Когда мы заносим новый элемент в стек, то он помещается поверх прежней вершины и теперь уже сам находится в вершине стека. Выбрать элемент можно только из вершины стека; при этом выбранный элемент исключается из стека, а в его вершине оказывается элемент, который был занесен в стек перед выбранным из него элементом (структура с ограниченным доступом к данным).
Графически стек можно представить следующим образом:

Первый элемент заносится вниз стека . Выборка из стека осуществляется с вершины, поэтому стек является структурой с ограниченным доступом.
Операции, производимые над стеками:
Push(S,I), где S - идентификатор стека, I - заносимый элемент.
Pop(S)
Empty(S)
StackTop(S)
Пример реализации стека на Паскале с использованием одномерного массива:
type
Stack = Array[1..10] of Integer; {стек вместимостью 10 элементов типа Integer}
var
StackCount: Integer; {Переменная - указатель на вершину стека, ее начальное значение должно быть равно 0}
S: Stack; {Объявление стека}
Procedure Push(I: Integer; var S: Stack);
begin
Inc(StackCount);
S[StackCount]:=I;
end;
Procedure Pop(var I: Integer; S: Stack);
begin
I:=S[StackCount];
Dec(StackCount);
end;
Function Empty: Boolean;
begin
If I = 0 then Empty:=True Else Empty:=False;
end;
При выполнении операции выборки из стека сначала необходимо осуществить проверку на пустоту стека. Если он пуст, то Empty возвращает значение True. Если Empty возвращает False, то это означает, что стек не пуст и из него еще можно выбирать элементы.
Procedure StackTop(var I: Integer; S: Stack);
begin
I:=S[StackCount];
end;
Понятие очереди всем хорошо известно из повседневной жизни. Элементами очереди в общем случае являются заказы на то или иное обслуживание.
В программировании имеется структура данных, которая называется очередью. Эта структура данных используется, например, для моделирования реальных очередей с целью определения их характеристик при данном законе поступления заказов и дисциплине их обслуживания. По своему существу очередь является полустатической структурой- с течением времени и длина очереди, и состав могут изменяться.
На рис. 2. 13 приведена очередь, содержащая четыре элемента — А, В, С и D. Элемент А расположен в начале очереди, а элемент D — в ее конце. Элементы могут удаляться только из начала очереди, то есть первый помещаемый в очередь элемент удаляется первым. По этой причине очередь часто называют списком, организованным по принципу «первый размещенный первым удаляется» в противоположность принципу стековой организации — «последний размещенный первым удаляется».
Дисциплину обслуживания, в которой заказ, поступивший в очередь первым, выбирается первым для обслуживания (и удаляется из очереди), называется FIFO (First In First Out - Первым пришел, первым ушел). Очередь открыта с обеих сторон.
Таким образом, изъятие компонент происходит из начала очереди, а запись- в конец. В этом случае вводят два указателя: один - на начало очереди, второй- на ее конец.
Реальная очередь создается в памяти ЭВМ в виде одномерного массива с конечным числом элементов, при этом необходимо указать тип элементов очереди, а также необходима переменная в работе с очередью.

Физически очередь занимает сплошную область памяти и элементы следуют друг за другом, как в последовательном списке.
Операции, производимые над очередью:
Для очереди определены три примитивные операции. Операция insert (q,x) помещает элемент х в конец очереди q. Операция remove(q) удаляет элемент из начала очереди q и присваивает его значение переменной х. Третья операция, empty (q), возвращает значение true или false в зависимости от того, является ли данная очередь пустой или нет. Кроме того. Учитывая то, что полустатическая очередь реализуется на одномерном массиве, необходимо следить за возможностью его переполнения. Сэтой целью вводится опнрация full(q).
Операция insert может быть выполнена всегда, поскольку на количество элементов, которые может содержать очередь, никаких ограничений не накладывается. Операция remove, однако, применима только к непустой очереди, поскольку невозможно удалить элемент из очереди, не содержащей элементов. Результатом попытки удалить элемент из пустой очереди является возникновение исключительной ситуации потеря значимости. Операция empty, разумеется, выполнима всегда.
Пример реализации очереди в виде одномерного массива на Паскале:
const
MaxQ = ...
type
E = ...
Queue = Array [1..MaxQ] of E;
var
Q: Queue;
F, R: Integer;
{Указатель F указывает на начало очереди. Указатель R указывает на конец очереди. Если очередь пуста, то F = 1, а R = 0 (То есть R < F – условие пустоты очереди).}
Procedure Insert(I: Integer; var Q: Queue);
begin
Inc(R);
Q[R]:=I;
end;
Function Empty(Q: Queue): Boolean;
begin
If R < F then Empty:=True Else Empty:=False;
end;
Procedure Remove(var I: Integer; Q: Queue);
begin
If Not Empty(Q) then
begin
I:=Q[F];
Inc(F);
end;
end;
Пример работы с очередью с использованием стандартных процедур.
MaxQ = 5
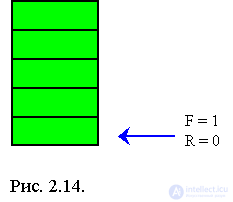
Производим вставку элементов A, B и C в очередь.
Insert(q, A);
Insert(q, B);
Insert(q, C);

Убираем элементы A и B из очереди.
Remove(q);
Remove(q);

К сожалению, при подобном представлении очереди, возможно возникновение абсурдной ситуации, при которой очередь является пустой, однако новый элемент разместить в ней нельзя (рассмотрите последовательность операций удаления и вставки, приводящую к такой ситуации). Ясно, что реализация очереди при помощи массива является неприемлемой.
Одним из решений возникшей проблемы может быть модификация операции remove таким образом, что при удалении очередного элемента вся очередь смещается к началу массива. Операция remove (q) может быть в этом случае реализована следующим образом.
X = q
For I =1 to R-1
q[I] =q[I+1]
next I
R =R-1
Переменная F больше не требуется, поскольку первый элемент массива всегда является началом очереди. Пустая очередь представлена очередью, для которой значение R равно нулю.
Однако этот метод весьма непроизводителен. Каждое удаление требует перемещения всех оставшихся в очереди элементов. Если очередь содержит 500 или 1000 элементов, то очевидно, что это весьма неэффективный способ. Далее, операция удаления элемента из очереди логически предполагает манипулирование только с одним элементом, т. е. с тем, который расположен в начале очереди. Реализация данной операции должна отражать именно этот факт, не производя при этом множества дополнительных действий.
Другой способ предполагает рассматривать массив, который содержит очередь в виде замкнутого кольца, а не линейной последовательности, имеющей начало и конец. Это означает, что первый элемент очереди следует сразу же за последним. Это означает, что даже в том случае, если последний элемент занят, новое значение может быть размещено сразу же за ним на месте первого элемента, если этот первый элемент пуст.
Организация кольцевой очереди.

Рассмотрим пример. Предположим, что очередь содержит три элемента - в позициях 3, 4 и 5 пятиэлементного массива. Этот случай, показанный на рис. 2.17. Хотя массив и не заполнен, последний элемент очереди занят.
Если теперь делается попытка поместить в очередь элемент G, то он будет записан в первую позицию массива, как это показано на рис. 2.17. Первый элемент очереди есть Q(3), за которым следуют элементы Q (4), Q(5) и Q(l).
К сожалению, при таком представлении довольно трудно определить, когда очередь пуста. Условие R
Одним из способов решения этой проблемы является введение соглашения, при котором значение F есть индекс элемента массива, немедленно предшествующего первому элементу очереди, а не индексу самого первого элемента. В этом случае, поскольку R содержит индекс последнего элемента очереди, условие F = R подразумевает, что очередь пуста.
Отметим, что перед началом работы с очередью, в F и R устанавливается значение последнего индекса массива, а не 0 и 1, поскольку при таком представлении очереди последний элемент массива немедленно предшествует первому элементу. Поскольку R = F, то очередь изначально пуста.
Основные операции с кольцевой очередью:
1. Вставка элемента q в очередь x.
Insert(q,x)
Remove(q)
Empty(q)
Операция empty (q) может быть записана следующим образом:
if F = R
then empty = true
else empty = false
endif
return
Операция remove (q) может быть записана следующим образом:
empty (q)
if empty = true
then print «выборка из пустой очереди»
stop
endif
if F =maxQ
then F =1
else F = F+1
endif
x = q(F)
return
Отметим, что значение F должно быть модифицировано до момента извлечения элемента.
Операция вставки insert (q,x).
Для того чтобы запрограммировать операцию вставки, должна быть проанализирована ситуация, при которой возникает переполнение. Переполнение происходит в том случае, если весь массив уже занят элементами очереди и при этом делается попытка разместить в ней еще один элемент. Рассмотрим, например, очередь на рис. 2. 17. В ней находятся три элемента — С, D и Е, соответственно расположенные в Q (3), Q (4) и Q (5). Поскольку последний элемент в очереди занимает позицию Q (5), значение R равно 5. Так как первый элемент в очереди находится в Q (3), значение F равно 2. На рис. 2. 17 в очередь помещается элемент G, что приводит к соответствующему изменению значения R. Если произвести следующую вставку, то массив становится целиком заполненным, и попытка произвести еще одну вставку приводит к переполнению. Это регистрируется тем фактом, что F = R, а это как раз и указывает на переполнение. Очевидно, что при такой реализации нет возможности сделать различие между пустой и заполненной очередью Разумеется, такая ситуация удовлетворить нас не может
Одно из решений состоит в том, чтобы пожертвовать одним элементом массива и позволить очереди расти до объема на единицу меньшего максимального. Так, если массив из 100 элементов объявлен как очередь, то очередь может содержать до 99 элементов. Попытка разместить в очереди 100-й элемент приведет к переполнению. Подпрограмма insert может быть записана следующим образом:
if R = max(q)
then R = 1
else R = R+1
endif
'проверка на переполнение
if R = F
then print «переполнение очереди»
stop
endif
q (r) =x
return
Проверка на переполнение в подпрограмме insert производится после установления нового значения для R, в то время как проверка на потерю значимости в подпрограмме remove производится сразу же после входа в подпрограмму до момента обновления значения F.
От английского DEQ - Double Ended Queue (Очередь с двумя концами)
Особенностью деков является то, что запись и считывание элементов может производиться с двух концов (рис. 2.18).

Дек можно рассматривать и в виде двух стеков, соединенных нижними границами. Возьмем пример, иллюстрирующий принцип построения дека. Рассмотрим состав на железнодорожной станции. Новые вагоны к составу можно добавлять либо к его концу, либо к началу. Аналогично, чтобы отсоединить от состава вагон, находящийся в середине, нужно сначала отсоединить все вагоны или вначале, или в конце состава, отсоединить нужный вагон, а затем присоединить их снова.
Операции над деками:
Контрольные вопросы
На этом все! Теперь вы знаете все про статические структуры данных, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое статические структуры данных, полустатические структуры данных и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных