2-3 дерево как структура данных кратко

Привет, Вы узнаете о том , что такое дерево, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое дерево, дерево b+ , настоятельно рекомендую прочитать все из категории Структуры данных.

2-3 дерево (англ. 2-3 tree) — структура данных, представляющая собой сбалансированное дерево поиска, такое что из каждого узла может выходить две или три ветви и глубина всех листьев одинакова. Является частным случаем B+ дерева.

Свойства

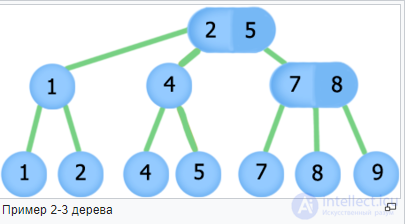
2-3 дерево — сбалансированное дерево поиска, обладающее следующими свойствами:

• нелистовые вершины имеют либо 2, либо 3 сына,
• нелистовая вершина, имеющая двух сыновей, хранит максимум левого поддерева. Нелистовая вершина, имеющая трех сыновей, хранит два значения. Первое значение хранит максимум левого поддерева, второе максимум центрального поддерева,
• сыновья упорядочены по значению максимума поддерева сына,
• все листья лежат на одной глубине,
• высота 2-3 дерева O(logn) , где n — количество элементов в дереве.

Узел имеющий 2 сына называется двухместным. Узел имеющий три сына называется трехместным.

Высота 2-3 дерева, содержащего n узлов, не может быть больше [log(n+1) - 1] (целая часть).

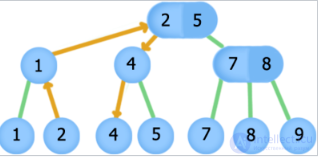
2-3 дерево поиска.

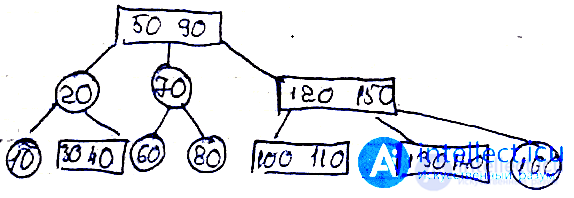
Ключи размещаются в соответствии со следующими правилами:

1 Двухместный внутренний узел имеет двух сыновей. Ключ двухместного узла должен быть больше, чем ключи левого поддерева и меньше, чем ключи правого поддерева.

2 Трехместный узел имеет трех сыновей. Должен содержать два элемента данных. Ключ S больше TL, но меньше TM, а ключ L больше, чем TM, но меньше TR.

3 Лист может содержать один или два элемента данных.

Операции

Введем следующие обозначения:

• root — корень 2-3 дерева.

Каждый узел дерева обладает полями:

• parent — родитель узла,
• sons — сыновья узла,
• keys — ключи узла,
• length — количество сыновей.

Поиск

• x — искомое значение,
• t — текущая вершина в дереве.

Изначально t=root. Будем просматривать ключи в узлах, пока узел не является листом. Рассмотрим два случая:

• у текущей вершины два сына. Если ее значение меньше xx, то t=t.sons t=t.sons , иначе t=t.sons .

• у текущей вершины три сына. Если второе значение меньше xx, то t=t.sons . Если первое значение меньше xx, то t=t.sons , иначе t=t.sons .

T search(T x):
  Node t = root
  while (t не является листом)
    if (t.length == 2)
      if (t.keys  < x)
        t = t.sons 
      else 
        t = t.sons 
    else if (t.keys  < x)
      t = t.sons 
    else if (t.keys  < x)
      t = t.sons 
    else 
      t = t.sons 
  return t.keys 

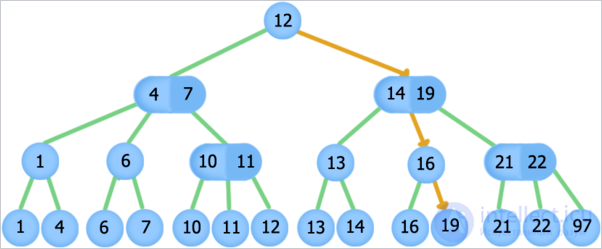
Поиск элемента 19, оранжевые стрелки обозначают путь по дереву при поиске

Вставка элемента

• x — добавляемое значение,
• t — текущая вершина в дереве. Об этом говорит сайт https://intellect.icu . Изначально t=root.

Если корня не существует — дерево пустое, то новый элемент и будет корнем (одновременно и листом). Иначе поступим следующим образом:

Найдем сперва, где бы находился элемент, применив search(x) Далее проверим есть ли у этого узла родитель, если его нет, то в дереве всего один элемент — лист. Возьмем этот лист и новый узел, и создадим для них родителя, лист и новый узел расположим в порядке возрастания.

Если родитель существует, то подвесим к нему еще одного сына. Если сыновей стало 4, то разделим родителя на два узла, и повторим разделение теперь для его родителя, ведь у него тоже могло быть уже 3 сына, а мы разделили и у него стало на 1 сына больше. (перед разделением обновим ключи).

function splitParent(Node t):
 if (t.length > 3) 
   Node a = Node(sons = {t.sons , t.sons }, keys = {t.keys }, parent = t.parent, length = 2)
   t.sons .parent = a
   t.sons .parent = a
   t.length = 2
   t.sons  = null
   t.sons  = null
   if (t.parent != null)
     t.parent[t.length] = a
     t.length++
     сортируем сыновей у t.parent
     splitParent(t.parent)
   else                   // мы расщепили корень, надо подвесить его к общему родителю, который будет новым корнем
    Node t = root
    root.sons  = t
    root.sons  = a
    t.parent = root
    a.parent = root
    root.length = 2
    сортируем сыновей у root

Если сыновей стало 33, то ничего не делаем. Далее необходимо восстановить ключи на пути от новой вершины до корня:

function updateKeys(Node t): 
  Node a = t.parent
  while (a != null)
   for i = 0 .. a.length - 1
     a.keys[i] = max(a.sons[i]) // max — возвращает максимальное значение в поддереве.
   a = a.parent                 // Примечание: max легко находить, если хранить максимум 
                                // правого поддерева в каждом узле — это значение и будет max(a.sons[i])

updateKeysupdateKeys необходимо запускать от нового узла. Добавление элемента:

function insert(T x):
  Node n = Node(x)
  if (root == null) 
   root = n
   return
  Node a = searchNode(x)     
  if (a.parent == null) 
    Node t = root
    root.sons  = t
    root.sons  = n
    t.parent = root
    n.parent = root
    root.length = 2
    сортируем сыновей у root
  else 
    Node p = a.parent
    p.sons[p.length] = n
    p.length++
    n.parent = p
    сортируем сыновей у p
    updateKeys(n) 
    split(n)
  updateKeys(n) 

Так как мы спускаемся один раз, и поднимаемся вверх при расщеплении родителей не более одного раза, то insertinsert работает за O(logn)O(log⁡n).

Примеры добавления:

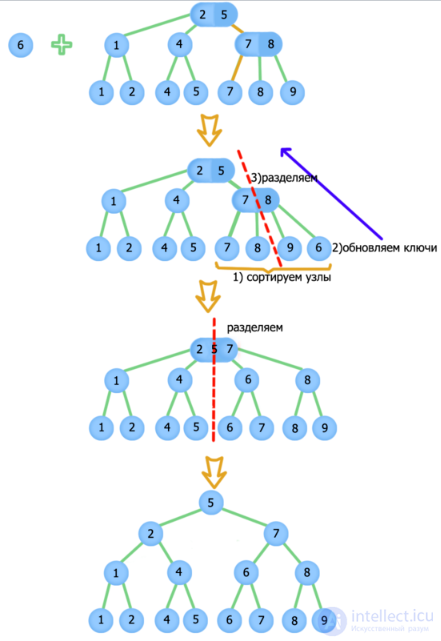
Добавление элемента с ключом 6

Удаление элемента

• x — значение удаляемого узла,
• t — текущий узел,
• b — брат t,
• p — отец t,
• np — соседний брат p,
• gp — отец p.

Пусть изначально t=searchNode(x) — узел, где находится xx.

Если у tt не существует родителя, то это корень (одновременно и единственный элемент в дереве). Удалим его.

Если pp существует, и у него строго больше 2 сыновей, то просто удалим t, а у p уменьшим количество детей.

Если у родителя tt два сына, рассмотрим возможные случаи (сперва везде удаляем t):

• npnp не существует, тогда мы удаляем одного из сыновей корня, следовательно, другой сын становится новым корнем,
• у gp оказалось 2 сына, у npnp оказалось 2 сына. Подвесим bb к npnp и удалим pp. Так как у gp — родителя p, оказалось тоже два сына, повторяем для pp такие же рассуждения,
• у gp оказалось 2 или 3 сына, у npnp оказалось 3 сына. Просто заберем ближайшего к нам сына у npnp и прицепим его к p. Восстановим порядок в сыновьях pp. Теперь у pp оказалось снова два сына и все узлы 2-3 дерева корректны,
• у gp оказалось 3 сына, у npnp оказалось 2 сына. Подвесим bb к npnp и удалим pp, а у gp уменьшим количество детей. Так как у npnp оказалось три сына, а у gp все еще больше одного сына, то все узлы 2-3 дерева корректны.

Обобщим алгоритм при удалении когда у родителя tt два сына:

• Если npnp не существует, то оказывается, что мы сейчас удаляем какого-то из сыновей корня (для определенности далее левого, с правым аналогично). Тогда теперь правый сын становится корнем. На этом удаление заканчивается.

• Если npnp существует, то удалим tt, а его брата (b) перецепим к npnp. Теперь у npnp могло оказаться 4 сына, поэтому повторим аналогичные действия из insertinsert: вызовем updateKeys(b) и splitParent(np) Теперь рекурсивно удалим p.

В результате мы получаем корректное по структуре 2-3 дерево, но у нас есть нарушение в ключах в узлах, исправим их с помощью updateKeys() , запустившись от b.

Удаление элемента с ключом 2

Следующий и предыдущий

• x — поисковый параметр,
• t — текущий узел.

В силу того, что наши узлы отсортированы по максимуму в поддереве, то следующий объект — это соседний лист справа. Попасть туда можно следующим образом: будем подниматься вверх, пока у нас не появится первой возможности свернуть направо вниз. Как только мы свернули направо вниз, будем идти всегда влево. Таким образом, мы окажемся в соседнем листе. Если мы не смогли ни разу свернуть направо вниз, и пришли в корень, то следующего объекта не существует. Случай с предыдущим симметричен.

 T next(T x):
   Node t = searchNode(x)
   if (t.keys  > x)  //x не было в дереве, и мы нашли следующий сразу
     return t.keys 
   while (t != null)
     t = t.parent
     if (можно свернуть направо вниз)
      в t помещаем вершину, в которую свернули
      while (пока t — не лист)
       t = t.sons 
     return t
   return t.keys 
    

Путь при поиске следующего элемента после 2

Нахождение m следующих элементов

B+ деревья, поддерживают операцию findfind, которая позволяет находить m следующих элементов. Наивная реализация выглядит следующим образом: будем вызывать mm раз поиск следующего элемента, такое решение работает за O(mlogn) . Но 2-3 деревья, позволяют находить m следующих элементов за O(m+logn) , что значительно ускоряет поиск при больших m. По построению, все листья у нас отсортированы в порядке возрастания, воспользуемся этим для нахождения m элементов. Нам необходимо связать листья, для этого модифицируем insert и delete Добавим к узлам следующие поля:

• right— указывает на правый лист,
• left— указывает на левый лист.

Пусть tt — добавленный узел. Изменим insert следующим образом: в самом конце, после того как мы уже обновили все ключи, найдем next(t) и запишем ссылку на него в t.rightt.right. Аналогично с левым.

Пусть t — удаляемый узел. Изменим delete следующим образом: в самом начале, до удаления tt, найдем следующий nextnext и запишем в next.left правый лист относительно t. С левым поступим аналогично.

В итоге, мы имеем двусвязный список в листьях, и чтобы нам вывести mm элементов, нам достаточно один раз найти нужный элемент и пробежаться вправо на mm элементов.

Вау!! 😲 Ты еще не читал? Это зря!

• B-дерево
• Splay-дерево
• АВЛ-дерево
• Декартово дерево
• Красно-черное дерево

Анализ данных, представленных в статье про дерево, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое дерево, дерево b+ и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных