Привет, сегодня поговорим про сортировка, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
сортировка , настоятельно рекомендую прочитать все из категории Структуры данных.
При обработке данных важно знать информационное поле данных и размещение их в машине.
Различают внутреннюю и внешнюю сортировку:
- внутренняя
сортировка - сортировка в оперативной памяти;
- внешняя сортировка - сортировка во внешней памяти.
Сортировка - это расположение данных в памяти в регулярном виде по их ключам. Регулярность рассматривают как возрастание (убывание) значения ключа от начала к концу в массиве.
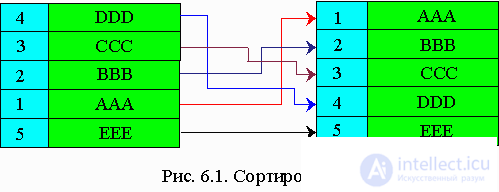
Если сортируемые записи занимают большой объем памяти, то их перемещение требует больших затрат. Для того, чтобы их уменьшить, сортировку производят в
таблице адресов ключей, делают перестановку указателей, т.е. сам массив не перемещается. Это
метод сортировки таблицы адресов.
При сортировке могут встретиться одинаковые ключи. В этом случае при сортировке желательно расположить после сортировки одинаковые ключи в том же порядке, что и в исходном файле. Это -
устойчивая сортировка.
Эффективность сортировки можно рассматривать с нескольких критериев:
время, затрачиваемое на сортировку;
объем оперативной памяти, требуемой для сортировки;
время, затраченное программистом на написание программы.
Выделяем первый критерий, поскольку будем рассматривать только методы сортировки «
на том же месте», то есть не резервируя для процесса сортировки дополнительную память. Эквивалентом затраченного на сортировку времени можно считать количество сравнений при выполнении сортировки и количество перемещений.
Порядок числа сравнения при сортировке лежит в пределах от О (n log n) до О (n
2); О (n) - идеальный и недостижимый случай.
Различают следующие методы сортировки:
строгие (прямые) методы;
улучшенные методы.
Строгие методы:
метод прямого включения;
метод прямого выбора;
метод прямого обмена.
Эффективность этих трех методов примерно одинакова.
6.1. Об этом говорит сайт https://intellect.icu . Сортировка методом прямого включения
Такой метод широко используется при игре в карты. Элементы мысленно делятся на уже готовую последовательность a
1,...,a
i-1 и исходную последовательность. При каждом шаге, начиная с i = 2 и увеличивая i каждый раз на единицу, из исхожной последовательности извлекается i-й элемент и перекладывается в готовую последовательность, при этом он вставляется на нужное место.На рис. 6.2 показан в качестве примера процесс сортировки с помощью включения шести случайно выбранных чисел. Алгоритм этой сортировки таков:
for i = 2 to n
x = a(i)
находим место среди а(1)…а(i) для включения х
next i
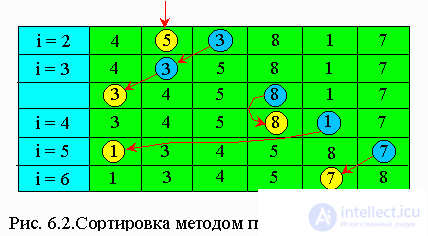
Для сортировки методом прямого включения пользуются следующими приемами:
Псевдокод:
Без барьера:
for i = 2 to n
x = a(i)
for j = i - 1 downto 1
if x < a(j )
then a( j + 1) = a(j )
else go to L
endif
next j
L: a( j + 1) = x
next i
return

С барьером:
for i = 2 to n
x = a(i)
a(0) = x {a(0) - барьер}
j = i - 1
while x < a(j ) do
a( j +1) = a(j )
j = j - 1
endwhile
a( j +1) = x
next i
return
|
Паскаль:
Без барьера:
for i:= 2 to n do
begin
x:= a(i);
for j:= i - 1downto 1 do
if x < a(j ) then
a(j +1):= a(j )
else goto 1;
end;
end;
1: a(j + 1):= x;
end;
end;
С барьером:
for i := 2 to n do
begin
x:= a(i);
a(0):= x; {a(0) - барьер}
j:= i - 1;
while x < a(j ) do
begin
a(j +1):= a(j );
j:=j - 1;
end;
a(j +1):= x;
end;
|
Эффективность алгоритмаЧисло сравнений ключей Ci при i- м просеивании самое большее равно i-1, самое меньшее - 1; если предположить, что все перестановки из N ключей равновероятны, то среднее число сравнений = i/2. Число же пересылок Mi=Ci+3 (включая барьер). Минимальные оценки встречаются в случае уже упорядоченной исходной последовательности элементов, наихудшие же оценки - когда они первоначально расположены в обратном порядке. В некотором смысле сортировка с помощью включения демонстрирует истинно естественное поведение. Ясно, что приведенный алгоритм описывает процесс устойчивой сортировки: порядок элементов с равными ключами при нем остается неизменным.
Количество сравнений в худшем случае, когда массив отсортирован противоположным образом, С
max = n(n - 1)/2, т. е. - О (n
2). Количество перестановок M
max = C
max + 3(n-1), т.е. - О (n
2). Если же массив уже отсортирован, то число сравнений и перестановок минимально: C
min = n-1; M
min = =3(n-1).
На этом все! Теперь вы знаете все про сортировка, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое сортировка
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Структуры данных
Из статьи мы узнали кратко, но содержательно про сортировка



Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных