Лекция
Сразу хочу сказать, что здесь никакой воды про суффструктуры, и только нужная информация. Для того чтобы лучше понимать что такое суффструктуры, суффиксный массив, суффиксное дерево , настоятельно рекомендую прочитать все из категории Структуры данных.
Суффструктуры - это структуры представления суффиксов строк, примерами таких структур являются суффиксерк дерево и суффиксны массив, Используются в алгоритмах поиска подстроки в строке, определении схожести строк и других.
Рассмотрим эти структуры подробнее.
Суффиксное дерево — бор, содержащий все суффиксы некоторой строки (и только их). Позволяет выяснять, входит ли строка w в исходную строку t, за время O(|w|), где |w| — длина строки w.
— непустое конечное множество символов, называемое алфавитом. Последовательность символов (возможно, пустая) из алфавита обозначается буквами r, s и t.
представляет собой перевернутую строку. Отдельные символы обозначаются буквами x, y или z.
— пустая строка. Символами из алфавита являются буквы a, b, …. Пока размер алфавита принимается постоянным. |t| обозначает длину строки t.
— все строки длины m,
и
.
Префикс w строки t — строка такая, что wv = t для некоторой (возможно, пустой) строки v. Префикс называется собственным, если |v| 0.
Суффикс w строки t — строка такая, что vw = t для некоторой (возможно, пустой) строки v. Суффикс называется собственным, если |v| 0. Например, для строки «substring» подстрока «sub» является собственным префиксом, «ring» — собственным суффиксом.
Подстрока w строки t называется правым ветвлением, если t может быть представлена как и
для некоторых строк
и
, а также букв x
y. Левое ветвление определяется аналогично. Например, для «eabceeabcd» подстрока «abc» является правым ветвлением, так как в обоих ее вхождениях в t справа от нее стоят различные символы, зато та же подстрока не является левым ветвлением, потому что слева от нее в обоих вхождениях стоит одинаковый символ «e».
-дерево T — корневое дерево с ребрами, помеченными последовательностями из
. Для каждого символа a из алфавита каждый узел в дереве T имеет не более одного ребра, метка которого начинается c символа a. Ребро от t до s с меткой v мы будем обозначать
.
Пусть k — узел -дерева T, тогда path(k) — строка, которая представляет собой конкатенацию всех меток ребер от корня до k. Мы назовем
местоположением w, для которого path(
) = w.
Так как каждая ветвь уникальна, если path(t) = w, мы можем обозначить узел t за . Поддерево узла
обозначается
.
Слова, которые представлены в -дереве T, задаются множеством, которое обозначается words(T). Слово w входит во множество words(T) тогда и только тогда, когда существует строка v (возможно, пустая) такая, что
— узел дерева T.
Если строка w входит в words(T), w = uv, — узел дерева T, пару
будем называть ссылочной парой w по отношению к дереву T. Если u — наидлиннейший префикс такой, что
— ссылочная пара, мы будем называть
канонической ссылочной парой. Тогда мы будем писать
. Местоположение
называется явным, если |v| = 0, и неявным в противном случае.
-дерево T, в котором каждое ребро помечено одиночным символом, называется атомарным (для него каждое местоположение является явным).
-дерево T, в котором каждый узел является либо корнем, либо листом или узлом ветвления, называется компактным.
Атомарное -дерево также называют
(луч). Атомарное и компактное
-дерево однозначно определены словами, которые они содержат.
Суффиксное дерево для строки t — это -дерево такое, что words(T) = {w| w — подслово t}. Для строки t атомарное суффиксное дерево обозначается ast(t), компактное суффиксное дерево обозначается cst(t).
Обратное префиксное дерево строки t — это суффиксное дерево для строки .
Вложенный суффикс — суффикс, который входит в строку t где-нибудь еще. Наидлиннейший вложенный суффикс называется активным суффиксом строки t.
Лемма. Местоположение w явно в компактном суффиксном дереве тогда и только тогда, когда w является не вложенным суффиксом t или w — правое ветвление.
Доказательство. . Если
явно, то это может быть либо лист, либо вершина ветвления или корень (в этом случае
и w — вложенный суффикс t).
Если — лист, тогда также является и суффиксом t. Значит, это должен быть не вложенный суффикс, так как иначе он появился бы где-нибудь еще в строке t:
v — суффикс t такой, что w — префикс v. Этот узел не может быть листом.
Если — узел ветвления, тогда должны существовать, по меньшей мере, два выходящих ребра из
с различными метками. Это означает, что существуют два различных суффикса u, v, что w — префикс u и w — префикс v, где v = wxs, u =
, x
. Следовательно, w — правое ветвление.
. Если w является не вложенным суффиксом t, это должен быть лист. Если w — правое ветвление, то имеются два суффикса u и v, u = wxs, v =
, x
, тогда w является узлом ветвления. Лемма доказана.
Теперь легко видеть, почему ответ на вопрос, входит ли слово w в строку t, может быть найден за время O(|w|): нужно только проверить, является ли w местоположением (явным или неявным) в cst(t).
Метки ребер должны представлять собой указатели на положение в строке, чтобы суффиксное дерево расходовало память размером O(n). Метка (p, q) ребра означает подстроку или пустую строку, если p > q.
Укконен вводит название открытые ребра для ребер, заканчивающихся в листьях. Пометки открытых ребер записывают как (p, ) вместо (p, |t|), где
— длина, всегда большая, чем |t|.
Пусть T — -дерево. Пусть
— узел T, v — наидлиннейший суффикс w такой, что
— также узел T. Непомеченное ребро от
до
называется суффиксным звеном. Если v = w, оно называется атомарным.
Утверждение. В ast(t) и cst(t$), где $ t, все суффиксные звенья являются атомарными.
Доказательство. Символ $ называется символом-стражем. Первая часть (для ast(t)) следует из определения, так как местоположения являются явными. Для доказательства второй (случай cst(t)) части мы должны показать, что для каждого узла
также является узлом cst(t). Если
— узел cst(t), то является либо листом, либо узлом ветвления. Если является листом, тогда aw — не вложенный суффикс t. Благодаря символу-стражу, из леммы следует, что все суффиксы (включая корень, пустой суффикс) являются явными, так как только корень — вложенный суффикс. Поэтому w является листом или корнем. Если
— узел ветвления, тогда aw — правое ветвление, как и w. Следовательно, местоположение
явно по лемме. Утверждение доказано.
Как следует из этого доказательства, символ-страж гарантирует существование листьев для всех суффиксов. С таким символом не может быть вложенных суффиксов, кроме пустого. Если мы опустим символ-страж, некоторые суффиксы могут стать вложенными, и их местоположения станут неявными.
Утверждение. Компактное суффиксное дерево может быть представлено в виде, требующем O(n) памяти.
Доказательство. Суффиксное дерево содержит не более одного листа на каждый суффикс (в точности один с символом-стражем). Каждый внутренний узел должен быть узлом ветвления, следовательно, внутренний узел имеет по меньшей мере двух потомков. Каждое ветвление увеличивает число листьев по меньшей мере на единицу, поэтому мы имеем не более n внутренних узлов и не более n листьев.
Для представления строк, являющихся метками ребер, мы используем индексацию в исходной строке, как описано выше. Каждый узел имеет не более одного предка и, таким образом, общее число ребер не превышает 2n.
Аналогично, каждый узел имеет не более одного суффиксного звена, тогда общее число суффиксных звеньев также ограничено числом 2n. Утверждение доказано.
Как пример суффиксного дерева с 2n-1 вершинами можно рассмотреть дерево для слова . Размер атомарного суффиксного дерева для строки t составляет O(
).
Алгоритм mcc начинает работу с пустого дерева и добавляет суффиксы начиная с самого длинного. Алгоритм mcc не является on-line алгоритмом, то есть для его работы необходима вся строка целиком. Об этом говорит сайт https://intellect.icu . Для корректной работы требуется, чтобы строка завершалась специальным символом, отличным от других, так, чтобы ни один суффикс не являлся префиксом другого суффикса. Каждому суффиксу в дереве будет соответствовать лист. Для алгоритма мы определим — текущий суффикс (на шаге
),
(голова) — наибольший префикс суффикса
, который является также префиксом другого суффикса
, где
.
(хвост) определим как
.
Ключевой идеей алгоритма mcc является соотношение между и
.
Лемма. Если где
— буква алфавита,
— строка (может быть пустая), тогда
— префикс
.
Доказательство. Пусть . Тогда существует
,
, такой, что
является как префиксом
, так и префиксом
. Тогда
— префикс
и
, следовательно,
является префиксом головы
. Лемма доказана.
Мы знаем местоположение , и если мы будем иметь суффиксное звено, то можем быстро перейти к местоположению
— префикса головы
без необходимости находить путь от корня дерева. Но местоположение }
могло бы не являться явным (если местоположение
не было явным на предыдущем шаге) и суффиксное звено могло бы быть еще не установлено для узла
. Решение, данное МакКреем, находит узел
за два шага: «повторное сканирование» («rescanning») и «сканирование» («scanning»). Мы проходим дерево наверх от узла
пока не найдем суффиксное звено, следуем по нему и затем применяем повторное сканирование пути до местоположения
(которое является простым, потому что мы знаем длину
и это местоположение существует, так что мы не должны читать полные метки ребер, двигаясь вниз по дереву, мы можем просто проверять только начальные буквы и длину слов).

Рисунок демонстрирует эту идею. Вместо попытки найти путь от корня до узла , алгоритм переходит до
, следует суффиксному звену до
, проводит повторное сканирование пути до (возможно неявного) местоположения
и остается найти путь до
, проходя посимвольно.
Алгоритм состоит из трех частей.
1. Сначала он определяет структуру предыдущей головы, находит следующее доступное суффиксное звено и следует по нему.
2. Затем он повторно сканирует часть предыдущей головы, для которой длина является известной (эта часть названа ).
3. Наконец алгоритм устанавливает суффиксное звено для , сканирует оставшуюся часть
(названную
) и добавляет новый лист для
.
Узел ветвления создается во второй фазе повторного сканирования, если не существует местоположения . В этом случае сканирование не является необходимым, потому что если
была бы длиннее чем
, тогда
являлось бы правым ветвлением, но по лемме }
является также правым ветвлением, так узел
уже должен существовать. Узел создается в третьей фазе, если местоположение
еще не явно.
Обратите внимание, что если тогда
и узнается одинаково быстро, как следуя суффиксному звену согласно строке 7 алгоритма.
Процедура Rescan ищет местоположение . Если местоположение
еще не явно, добавляется новый узел. Этот случай имеет место, когда голова (
) просмотрена целиком: если голова длиннее (и узел уже определен), }
должно являться префиксом более чем двух суффиксов и также является левым ветвлением
. Местоположение
может являться только явным, если этот узел уже является узлом ветвления, и если
не было левым ветвлением тогда
, должно быть, был длиннее, потому что встретился более длинный префикс.
Процедура Scan производит поиск в глубину дерева и возвращает позицию.

Алгоритм, который изобрел Эско Укконен для построения суффиксного дерева за линейное время, вероятно, самый простой из таких алгоритмов. Простота происходит оттого, что алгоритм можно представить сначала как простой, но неэффективный метод, который с помощью нескольких приемов реализации на уровне «здравого смысла» достигает уровня лучших алгоритмов по времени счета в наихудших условиях.
Для алгоритма Укконена нам потребуются
1) Неявные суффиксные деревья 2) Общее описание алгоритма 3) Оптимизация алгоритма
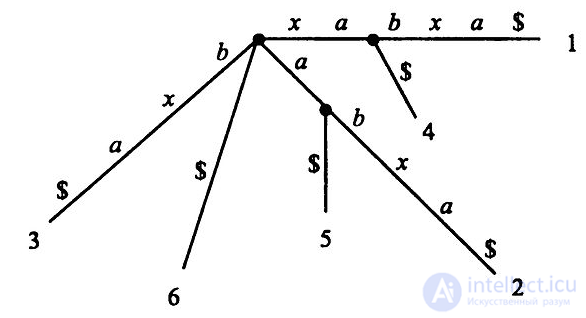
Суффиксное дерево для строки xabxa$

Неявное суффиксное дерево для строки xabxa$
Алгоритм Укконена строит последовательность неявных суффиксных деревьев, последнее из которых преобразуется в настоящее суффиксное дерево строки S.
Неявное суффиксное дерево строки S — это дерево, полученное из суффиксного дерева S$ удалением всех вхождений терминального символа $ из меток дуг дерева, удалением после этого дуг без меток и удалением затем вершин, имеющих меньше двух детей. Неявное суффиксное дерево префикса S[l..i] строки S аналогично получается из суффиксного дерева для S[l..i]$ удалением символов $, дуг и вершин, как описано выше.
Неявное суффиксное дерево для любой строки S будет иметь меньше листьев, чем суффиксное дерево для строки S$, в том и только том случае, если хотя бы один из суффиксов S является префиксом другого суффикса. Терминальный символ $ был добавлен к концу S как раз во избежание этой ситуации. В определении настоящего суффиксного дерева это очень важный момент. Однако если S заканчивается символом, который больше нигде в S не появляется, то неявное суффиксное дерево для S будет иметь лист для каждого суффикса и, следовательно, будет настоящим суффиксным деревом.
Хотя неявное суффиксное дерево может иметь листья не для всех суффиксов, в нем закодированы все суффиксы S — каждый произносится символами какого-либо пути от корня этого неявного суффиксного дерева. Однако если этот путь не кончается листом, то не будет маркера, обозначающего конец пути. Таким образом, неявные суффиксные деревья сами по себе несколько менее информативны, чем настоящие. Мы будем использовать их только как вспомогательное средство в алгоритме Укконена, чтобы получить настоящее суффиксное дерево для S.
Алгоритм Укконена строит неявное суффиксное дерево Ti для каждого префикса S[l..i] строки S, начиная с T1 и увеличивая i на единицу, пока не будет построено Tm. Настоящее суффиксное дерево для S получается из Tm, и вся работа требует времени О(m). Мы объясним алгоритм Укконена, представив сначала метод, с помощью которого все деревья строятся за время O(m³), а затем оптимизируем реализацию этого метода так, что будет достигнута заявленная скорость.
Чтобы превратить это общее описание в алгоритм, мы должны точно указать, как выполнять продолжение суффикса. Пусть S[j..i] = β — суффикс S[1..i]. В продолжении j, когда алгоритм находит конец β в текущем дереве, он продолжает β, чтобы обеспечить присутствие суффикса βS(i + 1) в дереве. Алгоритм действует по одному из следующих трех правил.
Правило 1. В текущем дереве путь β кончается в листе. Это значит, что путь от корня с меткой β доходит до конца некоторой «листовой» дуги (дуги, входящей в лист). При изменении дерева нужно добавить к концу метки этой листовой дуги символ S(i + 1).
Правило 2. Ни один путь из конца строки β не начинается символом S(i + 1), но по крайней мере один начинающийся оттуда путь имеется. В этом случае должна быть создана новая листовая дуга, начинающаяся в конце β, помеченная символом S(i + 1). При этом, если β кончается внутри дуги, должна быть создана новая вершина. Листу в конце новой листовой дуги сопоставляется номер j. Таким образом, в правиле 2 возможно два случая.
Правило 3. Некоторый путь из конца строки β начинается символом S(i + 1). В этом случае строка βS(i + 1) уже имеется в текущем дереве, так что ничего не надо делать (в неявном суффиксном дереве конец суффикса не нужно помечать явно).
Суффиксный массив — лексикографически отсортированный массив всех суффиксов строки. Эта структура данных была разработана Джином Майерсом и Уди Манбером как более экономная альтернатива суффиксному дереву с точки зрения необходимой памяти. Она часто применяется там, где необходим быстрый поиск подстрок, например в преобразовании Барроуза — Уилера (BWT), а также в качестве структуры данных в поисковом индексе.
Дана строка 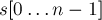 длины
длины 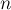 .
.
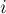 -ым суффиксом строки называется подстрока
-ым суффиксом строки называется подстрока 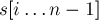 ,
,  .
.
Тогда суффиксным массивом строки 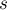 называется перестановка индексов суффиксов
называется перестановка индексов суффиксов  ,
, 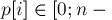 , которая задает порядок суффиксов в порядке лексикографической сортировки. Иными словами, нужно выполнить сортировку всех суффиксов заданной строки.
, которая задает порядок суффиксов в порядке лексикографической сортировки. Иными словами, нужно выполнить сортировку всех суффиксов заданной строки.
Например, для строки 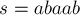 суффиксный массив будет равен:
суффиксный массив будет равен:
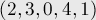
В 1989 году Манбер и Майерс опубликовали статью, в которой описали такую структуру данных, как суффиксный массив, и как ее применять для поиска подстрок. Суффиксный массив — это массив лексикографически отсортированных суффиксов строк (если терминология незнакома, то можно глянуть раздел «постановка задачи» в этой статье). Вообще говоря, хранить сами суффиксы смысла нет, достаточно хранить позицию начала данного суффикса, но определение массива так легче воспринимается. Вот пример для строки «mississippi»:
Рассмотрим строку «abracadabra» длиной 11 символов.

Отсортированный список ее суффиксов:

Суффиксный массив этой строки — {11,8,1,4,6,9,2,5,7,10,3}, потому что суффикс «a» начинается с 11-го знака, суффикс «abra» — с 8-го, и так далее, вплоть до последнего суффикса «racadabra», который начинается с третьего символа исходного слова.
Теперь с помощью этого массива можно легко найти все подстроки. Например, если нужно найти подстроку «ab», достаточно найти все суффиксы, которые начинаются на «ab». За счет сортировки по алфавиту, они находятся рядом друг с другом. Используя бинарный поиск, мы находим 2-й и 3-й суффиксы «abra» и «abracadabra», которым соответствуют 2-й и 3-й элемент суффиксного массива (8 и 1). Это означает, что искомая подстрока «ab» встречается на первом и восьмом символе в исходном слове.
Вышеописанный алгоритм производит сортировку циклических сдвигов (если к строке не приписывать доллар), а потому 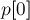 даст искомую позицию наименьшего циклического сдвига. Время работы —
даст искомую позицию наименьшего циклического сдвига. Время работы — 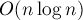 .
.
Пусть требуется в тексте 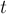 искать строку
искать строку 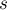 в режиме онлайн (т.е. заранее строку
в режиме онлайн (т.е. заранее строку 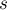 нужно считать неизвестной). Построим суффиксный массив для текста
нужно считать неизвестной). Построим суффиксный массив для текста 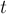 за
за 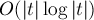 . Теперь подстроку
. Теперь подстроку 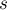 будем искать следующим образом: заметим, что искомое вхождение должно быть префиксом какого-либо суффикса
будем искать следующим образом: заметим, что искомое вхождение должно быть префиксом какого-либо суффикса 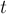 . Поскольку суффиксы у нас упорядочены (это дает нам суффиксный массив), то подстроку
. Поскольку суффиксы у нас упорядочены (это дает нам суффиксный массив), то подстроку 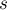 можно искать бинарным поиском по суффиксам строки. Сравнение текущего суффикса и подстроки
можно искать бинарным поиском по суффиксам строки. Сравнение текущего суффикса и подстроки 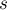 внутри бинарного поиска можно производить тривиально, за
внутри бинарного поиска можно производить тривиально, за 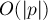 . Тогда асимптотика поиска подстроки в тексте становится
. Тогда асимптотика поиска подстроки в тексте становится  .
.
Требуется по заданной строке 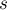 , произведя некоторый ее препроцессинг, научиться за
, произведя некоторый ее препроцессинг, научиться за 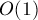 отвечать на запросы сравнения двух произвольных подстрок (т.е. проверка, что первая подстрока равна/меньше/больше второй).
отвечать на запросы сравнения двух произвольных подстрок (т.е. проверка, что первая подстрока равна/меньше/больше второй).
Построим суффиксный массив за 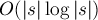 , при этом сохраним промежуточные результаты: нам понадобятся массивы
, при этом сохраним промежуточные результаты: нам понадобятся массивы 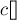 от каждой фазы. Поэтому памяти потребуется тоже
от каждой фазы. Поэтому памяти потребуется тоже 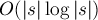 .
.
Используя эту информацию, мы можем за 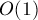 сравнивать любые две подстроки длины, равной степени двойки: для этого достаточно сравнить номера классов эквивалентности из соответствующей фазы. Теперь надо обобщить этот способ на подстроки произвольной длины.
сравнивать любые две подстроки длины, равной степени двойки: для этого достаточно сравнить номера классов эквивалентности из соответствующей фазы. Теперь надо обобщить этот способ на подстроки произвольной длины.
Пусть теперь поступил очередной запрос сравнения двух подстрок длины  с началами в индексах
с началами в индексах 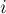 и
и 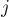 . Найдем наибольшую длину блока, помещающегося внутри подстроки такой длины, т.е. наибольшее
. Найдем наибольшую длину блока, помещающегося внутри подстроки такой длины, т.е. наибольшее 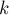 такое, что
такое, что 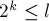 . Тогда сравнение двух подстрок можно заменить сравнением двух пар перекрывающихся блоков длины
. Тогда сравнение двух подстрок можно заменить сравнением двух пар перекрывающихся блоков длины 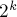 : сначала надо сравнить два блока, начинающихся в позициях
: сначала надо сравнить два блока, начинающихся в позициях 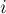 и
и 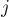 , а при равенстве — сравнить два блока, заканчивающихся в позициях
, а при равенстве — сравнить два блока, заканчивающихся в позициях 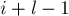 и
и  :
:
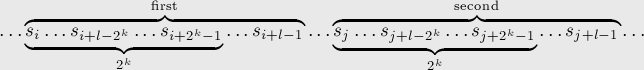
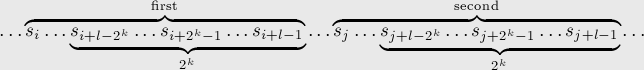
Таким образом, реализация получается примерно такой (здесь считается, что вызывающая процедура сама вычисляет 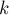 , поскольку сделать это за константное время не так легко (по-видимому, быстрее всего — предпосчетом), но в любом случае это не имеет отношения к применению суффиксного массива):
, поскольку сделать это за константное время не так легко (по-видимому, быстрее всего — предпосчетом), но в любом случае это не имеет отношения к применению суффиксного массива):
Требуется по заданной строке 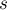 , произведя некоторый ее препроцессинг, научиться за
, произведя некоторый ее препроцессинг, научиться за 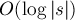 отвечать на запросы наибольшего общего префикса (longest common prefix, lcp) для двух произвольных суффиксов с позициями
отвечать на запросы наибольшего общего префикса (longest common prefix, lcp) для двух произвольных суффиксов с позициями 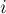 и
и 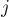 .
.
Способ, описываемый здесь, требует 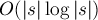 дополнительной памяти; другой способ, использующий линейный объем памяти, но неконстантное время ответа на запрос, описан в следующем разделе.
дополнительной памяти; другой способ, использующий линейный объем памяти, но неконстантное время ответа на запрос, описан в следующем разделе.
Построим суффиксный массив за 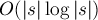 , при этом сохраним промежуточные результаты: нам понадобятся массивы
, при этом сохраним промежуточные результаты: нам понадобятся массивы 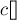 от каждой фазы. Поэтому памяти потребуется тоже
от каждой фазы. Поэтому памяти потребуется тоже 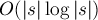 .
.
Пусть теперь поступил очередной запрос: пара индексов 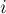 и
и 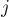 . Воспользуемся тем, что мы можем за
. Воспользуемся тем, что мы можем за 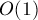 сравнивать любые две подстроки длины, являющейся степенью двойки. Для этого будем перебирать степень двойки (от большей к меньшей), и для текущей степени проверять: если подстроки такой длины совпадают, то к ответу прибавить эту степень двойки, а наибольший общий префикс продолжим искать справа от одинаковой части, т.е. к
сравнивать любые две подстроки длины, являющейся степенью двойки. Для этого будем перебирать степень двойки (от большей к меньшей), и для текущей степени проверять: если подстроки такой длины совпадают, то к ответу прибавить эту степень двойки, а наибольший общий префикс продолжим искать справа от одинаковой части, т.е. к 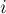 и
и 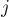 надо прибавить текущую степень двойки.
надо прибавить текущую степень двойки.
Реализация:
Здесь через 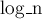 обозначена константа, равная логарифму
обозначена константа, равная логарифму 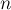 по основанию 2, округленному вниз.
по основанию 2, округленному вниз.
Требуется по заданной строке 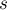 , произведя некоторый ее препроцессинг, научиться отвечать на запросы наибольшего общего префикса (longest common prefix, lcp) для двух произвольных суффиксов с позициями
, произведя некоторый ее препроцессинг, научиться отвечать на запросы наибольшего общего префикса (longest common prefix, lcp) для двух произвольных суффиксов с позициями 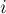 и
и 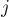 .
.
В отличие от предыдущего метода, описываемый здесь будет выполнять препроцессинг строки за 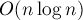 времени с
времени с 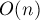 памяти. Результатом этого препроцессинга будет являться массив (который сам по себе является важным источником информации о строке, и потому использоваться для решения других задач). Ответы же на запрос будут производиться как результат выполнения запроса RMQ (минимум на отрезке, range minimum query) в этом массиве, поэтому при разных реализациях можно получить как логарифмическое, так и константное времена работы.
памяти. Результатом этого препроцессинга будет являться массив (который сам по себе является важным источником информации о строке, и потому использоваться для решения других задач). Ответы же на запрос будут производиться как результат выполнения запроса RMQ (минимум на отрезке, range minimum query) в этом массиве, поэтому при разных реализациях можно получить как логарифмическое, так и константное времена работы.
Базой для этого алгоритма является следующая идея: найдем каким-нибудь образом наибольшие общие префиксы для каждой соседней в порядке сортировки пары суффиксов. Иными словами, построим массив 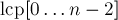 , где
, где 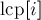 равен наибольшему общему префиксу суффиксов
равен наибольшему общему префиксу суффиксов 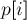 и
и  . Этот массив даст нам ответ для любых двух соседних суффиксов строки. Тогда ответ для любых двух суффиксов, не обязательно соседних, можно получить по этому массиву. В самом деле, пусть поступил запрос с некоторыми номерами суффиксов
. Этот массив даст нам ответ для любых двух соседних суффиксов строки. Тогда ответ для любых двух суффиксов, не обязательно соседних, можно получить по этому массиву. В самом деле, пусть поступил запрос с некоторыми номерами суффиксов 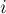 и
и 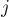 . Найдем эти индексы в суффиксном массиве, т.е. пусть
. Найдем эти индексы в суффиксном массиве, т.е. пусть 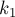 и
и  — их позиции в массиве
— их позиции в массиве  (упорядочим их, т.е. пусть
(упорядочим их, т.е. пусть 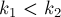 ). Тогда ответом на данный запрос будет минимум в массиве
). Тогда ответом на данный запрос будет минимум в массиве 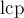 , взятый на отрезке
, взятый на отрезке  . В самом деле, переход от суффикса
. В самом деле, переход от суффикса 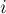 к суффиксу
к суффиксу 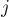 можно заменить целой цепочкой переходов, начинающейся с суффикса
можно заменить целой цепочкой переходов, начинающейся с суффикса 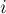 и заканчивающейся в суффиксе
и заканчивающейся в суффиксе 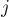 , но включающей в себя все промежуточные суффиксы, находящиеся в порядке сортировки между ними.
, но включающей в себя все промежуточные суффиксы, находящиеся в порядке сортировки между ними.
Таким образом, если мы имеем такой массив 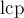 , то ответ на любой запрос наибольшего общего префикса сводится к запросу минимума на отрезке массива
, то ответ на любой запрос наибольшего общего префикса сводится к запросу минимума на отрезке массива 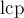 . Эта классическая задача минимума на отрезке (range minimum query, RMQ) имеет множество решений с различными асимптотиками, описанные здесь.
. Эта классическая задача минимума на отрезке (range minimum query, RMQ) имеет множество решений с различными асимптотиками, описанные здесь.
Итак, основная наша задача — построение этого массива 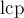 . Строить его мы будем по ходу алгоритма построения суффиксного массива: на каждой текущей итерации будем строить массив
. Строить его мы будем по ходу алгоритма построения суффиксного массива: на каждой текущей итерации будем строить массив 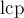 для циклических подстрок текущей длины.
для циклических подстрок текущей длины.
После нулевой итерации массив 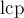 , очевидно, должен быть нулевым.
, очевидно, должен быть нулевым.
Пусть теперь мы выполнили  -ю итерацию, получили от нее массив
-ю итерацию, получили от нее массив 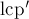 , и должны на текущей
, и должны на текущей 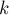 -й итерации пересчитать этот массив, получив новое его значение
-й итерации пересчитать этот массив, получив новое его значение 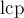 . Как мы помним, в алгоритме построения суффиксного массива циклические подстроки длины
. Как мы помним, в алгоритме построения суффиксного массива циклические подстроки длины 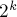 разбивались пополам на две подстроки длины
разбивались пополам на две подстроки длины 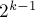 ; воспользуемся этим же приемом и для построения массива
; воспользуемся этим же приемом и для построения массива 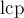 .
.
Итак, пусть на текущей итерации алгоритм вычисления суффиксного массива выполнил свою работу, нашел новое значение перестановки  подстрок. Будем теперь идти по этому массиву и смотреть пары соседних подстрок:
подстрок. Будем теперь идти по этому массиву и смотреть пары соседних подстрок: 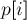 и
и  ,
,  . Разбивая каждую подстроку пополам, мы получаем две различных ситуации: 1) первые половинки подстрок в позициях
. Разбивая каждую подстроку пополам, мы получаем две различных ситуации: 1) первые половинки подстрок в позициях 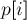 и
и  различаются, и 2) первые половинки совпадают (напомним, такое сравнение можно легко производить, просто сравнивая номера классов
различаются, и 2) первые половинки совпадают (напомним, такое сравнение можно легко производить, просто сравнивая номера классов 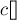 с предыдущей итерации). Рассмотрим каждый из этих случаев отдельно.
с предыдущей итерации). Рассмотрим каждый из этих случаев отдельно.
1) Первые половинки подстрок различались. Заметим, что тогда на предыдущем шаге эти первые половинки необходимо были соседними. В самом деле, классы эквивалентности не могли исчезать (а могут только появляться), поэтому все различные подстроки длины 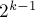 дадут (в качестве первых половинок) на текущей итерации различные подстроки длины
дадут (в качестве первых половинок) на текущей итерации различные подстроки длины 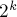 , и в том же порядке. Таким образом, для определения
, и в том же порядке. Таким образом, для определения 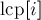 в этом случае надо просто взять соответствующее значение из массива
в этом случае надо просто взять соответствующее значение из массива 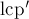 .
.
2) Первые половинки совпадали. Тогда вторые половинки могли как совпадать, так и различаться; при этом, если они различаются, то они совсем не обязательно должны были быть соседними на предыдущей итерации. Поэтому в этом случае нет простого способа определить 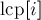 . Для его определения надо поступить так же, как мы и собираемся потом вычислять наибольший общий префикс для любых двух суффиксов: надо выполнить запрос минимума (RMQ) на соответствующем отрезке массива
. Для его определения надо поступить так же, как мы и собираемся потом вычислять наибольший общий префикс для любых двух суффиксов: надо выполнить запрос минимума (RMQ) на соответствующем отрезке массива 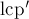 .
.
Оценим асимптотику такого алгоритма. Как мы видели при разборе этих двух случаев, только второй случай дает увеличение числа классов эквивалентности. Иными словами, можно говорить о том, что каждый новый класс эквивалентности появляется вместе с одним запросом RMQ. Поскольку всего классов эквивалентности может быть до 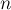 , то и искать минимум мы должны за асимптотику
, то и искать минимум мы должны за асимптотику 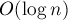 . А для этого надо использовать уже какую-то структуру данных для минимума на отрезке; эту структуру данных надо будет строить заново на каждой итерации (которых всего
. А для этого надо использовать уже какую-то структуру данных для минимума на отрезке; эту структуру данных надо будет строить заново на каждой итерации (которых всего 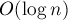 ). Хорошим вариантом структуры данных будет Дерево отрезков: его можно построить за
). Хорошим вариантом структуры данных будет Дерево отрезков: его можно построить за 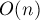 , а потом выполнять запросы за
, а потом выполнять запросы за 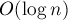 , что как раз и дает нам итоговую асимптотику
, что как раз и дает нам итоговую асимптотику 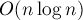 .
.
Реализация:
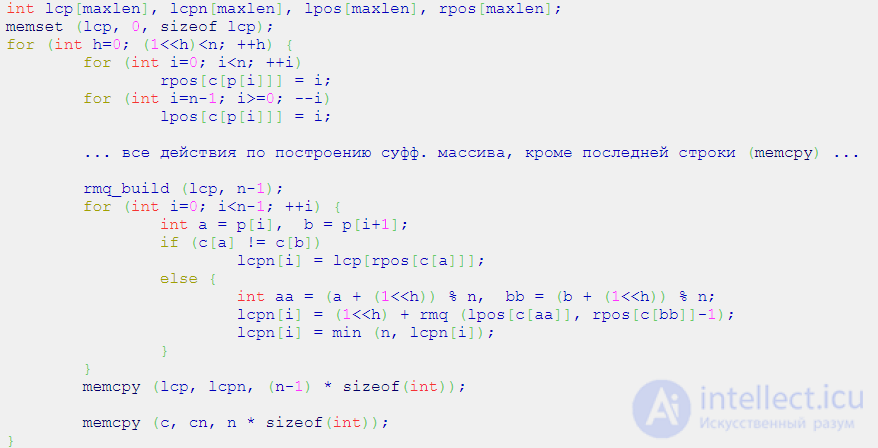
Здесь помимо массива  вводится временный массив
вводится временный массив 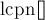 с его новым значением. Также поддерживается массив
с его новым значением. Также поддерживается массив  , который для каждой подстроки хранит ее позицию в перестановке
, который для каждой подстроки хранит ее позицию в перестановке  . Функция
. Функция 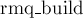 — некоторая функция, строящая структуру данных для минимума по массиву-первому аргументу, размер его передается вторым аргументом. Функция
— некоторая функция, строящая структуру данных для минимума по массиву-первому аргументу, размер его передается вторым аргументом. Функция 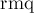 возвращает минимум на отрезке: с первого аргумента по второй включительно.
возвращает минимум на отрезке: с первого аргумента по второй включительно.
Из самого алгоритма построения суффиксного массива пришлось только вынести копирование массива 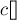 , поскольку во время вычисления
, поскольку во время вычисления 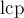 нам понадобятся старые значения этого массива.
нам понадобятся старые значения этого массива.
Стоит отметить, что наша реализация находит длину общего префикса для циклических подстрок, в то время как на практике чаще бывает нужной длина общего префикса для суффиксов в их обычном понимании. В этом случае надо просто ограничить значения 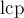 по окончании работы алгоритма:
по окончании работы алгоритма:
Для любых двух суффиксов длину их наибольшего общего префикса теперь можно найти как минимум на соответствующем отрезке массива 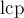 :
:
Выполним препроцессинг, описанный в предыдущем разделе: за 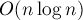 времени и
времени и 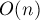 памяти мы для каждой пары соседних в порядке сортировки суффиксов найдем длину их наибольшего общего префикса. Найдем теперь по этой информации количество различных подстрок в строке.
памяти мы для каждой пары соседних в порядке сортировки суффиксов найдем длину их наибольшего общего префикса. Найдем теперь по этой информации количество различных подстрок в строке.
Для этого будем рассматривать, какие новые подстроки начинаются в позиции 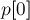 , затем в позиции
, затем в позиции 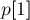 , и т.д. Фактически, мы берем очередной в порядке сортировки суффикс и смотрим, какие его префиксы дают новые подстроки. Тем самым мы, очевидно, не упустим из виду никакие из подстрок.
, и т.д. Фактически, мы берем очередной в порядке сортировки суффикс и смотрим, какие его префиксы дают новые подстроки. Тем самым мы, очевидно, не упустим из виду никакие из подстрок.
Пользуясь тем, что суффиксы у нас уже отсортированы, нетрудно понять, что текущий суффикс 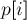 даст в качестве новых подстрок все свои префиксы, кроме совпадающих с префиксами суффикса
даст в качестве новых подстрок все свои префиксы, кроме совпадающих с префиксами суффикса  . Т.е. все его префиксы, кроме
. Т.е. все его префиксы, кроме 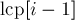 первых, дадут новые подстроки. Поскольку длина текущего суффикса равна
первых, дадут новые подстроки. Поскольку длина текущего суффикса равна 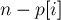 , то окончательно получаем, что текущий суффикс
, то окончательно получаем, что текущий суффикс 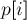 дает
дает 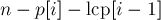 новых подстрок. Суммируя это по всем суффиксам (для самого первого,
новых подстрок. Суммируя это по всем суффиксам (для самого первого, 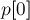 , отнимать нечего — прибавится просто
, отнимать нечего — прибавится просто 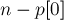 ), получаем ответ на задачу:
), получаем ответ на задачу:
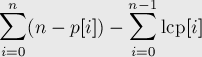
А как ты думаешь, при улучшении суффструктуры, будет лучше нам? Надеюсь, что теперь ты понял что такое суффструктуры, суффиксный массив, суффиксное дерево и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных