Лекция
Привет, сегодня поговорим про полустатические структуры данных, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое полустатические структуры данных, реализация строк, стеки и очереди и строки и деки , настоятельно рекомендую прочитать все из категории Структуры данных.
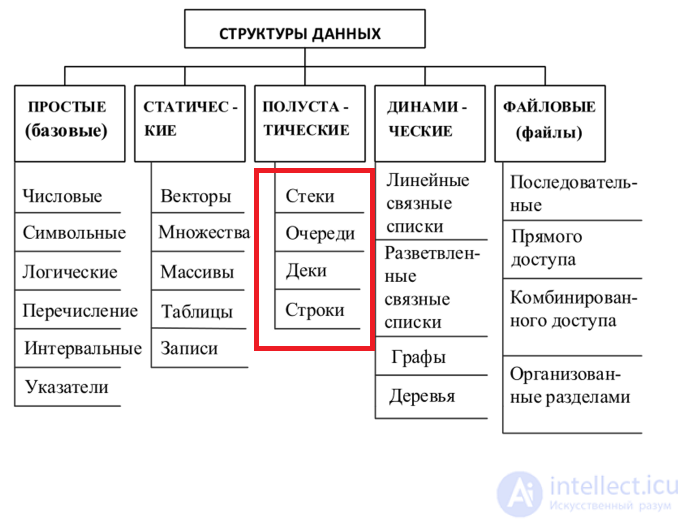
полустатические структуры данных характеризуются следующими признаками:
Если полустатическую структуру рассматривать на логическом уровне, то о ней можно сказать, что это последовательность данных, связанная отношениями линейного списка. Доступ к элементу может осуществляться по его порядковому номеру.
Физическое представление полустатических структур данных в памяти - это обычно последовательность слотов в памяти, где каждый следующий элемент расположен в памяти в следующем слоте (т.е. вектор). Физическое представление может иметь также вид однонаправленного связного списка (цепочки), где каждый следующий элемент адресуется указателем находящемся в текущем элементе. В пос- леднем случае ограничения на длину структуры гораздо менее строгие.
Стек - такой последовательный список с переменной длиной, включение и исключение элементов из которого выполняются только с одной стороны списка, называемого вершиной стека. Применяются и другие названия стека - магазин и очередь, функционирующая по принципу LIFO (Last - In - First- Out - "последним пришел - первым исключается"). Примеры стека: винтовочный патронный магазин, тупиковый железнодорожный разъезд для сортировки вагонов.
Основные операции над стеком - включение нового элемента (английское название push - заталкивать) и исключение элемента из стека (англ. pop - выскакивать).
Полезными могут быть также вспомогательные операции:
x:=pop(stack); push(stack,x).
Некоторые авторы рассматривают также операции включения/исключения элементов для середины стека, однако структура, для которой возможны такие операции, не соответствует стеку по определению.
Для наглядности рассмотрим небольшой пример, демонстрирующий принцип включения элементов в стек и исключения элементов из стека. На рис. 4.1 (а,б,с) изображены состояния стека:
Рис 4.1. Включение и исключение элементов из стека.
Как видно из рис. 4.1, стек можно представить, например, в виде стопки книг (элементов), лежащей на столе. Присвоим каждой книге свое название, например A,B,C,D... Тогда в момент времени, когда на столе книг нет, про стек аналогично можно сказать, что он пуст, т.е. не содержит ни одного элемента. Если же мы начнем последовательно класть книги одну на другую, то получим стопку книг (допустим, из n книг), или получим стек, в котором содержится n элементов, причем вершиной его будет являться элемент n+1. Удаление элементов из стека осуществляется аналогичным образом т. е. удаляется последовательно по одному элементу, начиная с вершины, или по одной книге из стопки.
При представлении стека в статической памяти для стека выделяется память, как для вектора. В дескрипторе этого вектора кроме обычных для вектора параметров должен находиться также указатель стека - адрес вершины стека. Указатель стека может указывать либо на первый свободный элемент стека, либо на последний записанный в стек элемент. (Все равно, какой из этих двух вариантов выбрать, важно в последствии строго придерживаться его при обработке стека.) В дальнейшем мы будем всегда считать, что указатель стека адресует первый свободный элемент и стек растет в сторону увеличения адресов.
При занесении элемента в стек элемент записывается на место, определяемое указателем стека, затем указатель модифицируется таким образом, чтобы он указывал на следующий свободный элемент (если указатель указывает на последний записанный элемент, то сначала модифицируется указатель, а затем производится запись элемента). Модификация указателя состоит в прибавлении к нему или в вычитании из него единицы (помните, что наш стек растет в сторону увеличения адресов.
Операция исключения элемента состоит в модификации указателя стека (в направлении, обратном модификации при включении) и выборке значения, на которое указывает указатель стека. После выборки слот, в котором размещался выбранный элемент, считается свободным.
Операция очистки стека сводится к записи в указатель стека начального значения - адреса начала выделенной области памяти.
Определение размера стека сводится к вычислению разности указателей: указателя стека и адреса начала области.
Программный модуль, представленный в примере 4.1, иллюстрирует операции над стеком, расширяющимся в сторону уменьшения адресов. Указатель стека всегда указывает на первый свободный элемент.
В примерах 4.1 и 4.3 предполагается, что в модуле будут уточнены определения предельного размера структуры и типа данных для элемента структуры:
const SIZE = ...;
type data = ...;
{==== Программный пример 4.1 ====}
{ Стек }
unit Stack;
Interface
const SIZE=...; { предельный размер стека }
type data = ...; { эл-ты могут иметь любой тип }
Procedure StackInit;
Procedure StackClr;
Function StackPush(a : data) : boolean;
Function StackPop(Var a : data) : boolean;
Function StackSize : integer;
Implementation
Var StA : array[1..SIZE] of data; { Стек - данные }
{ Указатель на вершину стека, работает на префиксное вычитание }
top : integer;
Procedure StackInit; {** инициализация - на начало }
begin top:=SIZE; end; {** очистка = инициализация }
Procedure StackClr;
begin top:=SIZE; end;
{ ** занесение элемента в стек }
Function StackPush(a: data) : boolean;
begin
if top=0 then StackPush:=false
else begin { занесение, затем - увеличение указателя }
StA[top]:=a; top:=top-1; StackPush:=true;
end; end; { StackPush }
{ ** выборка элемента из стека }
Function StackPop(var a: data) : boolean;
begin
if top=SIZE then StackPop:=false
else begin { указатель увеличивается, затем - выборка }
top:=top+1; a:=StA[top]; StackPop:=true;
end; end; { StackPop }
Function StackSize : integer; {** определение размера }
begin StackSize:=SIZE-top; end;
END.
Стек является чрезвычайно удобной структурой данных для многих задач вычислительной техники. Наиболее типичной из таких задач является обеспечение вложенных вызовов процедур.
Предположим, имеется процедура A, которая вызывает процедуру B, а та в свою очередь - процедуру C. Когда выполнение процедуры A дойдет до вызова B, процедура A приостанавливается и управление передается на входную точку процедуры B. Когда B доходит до вызова C, приостанавливается B и управление передается на процедуру C. Когда заканчивается выполнение процедуры C, управление должно быть возвращено в B, причем в точку, следующую за вызовом C. При завершении B управление должно возвращаться в A, в точку, следующую за вызовом B. Правильную последовательность возвратов легко обеспечить, если при каждом вызове процедуры записывать адрес возврата в стек. Так, когда процедура A вызывает процедуру B, в стек заносится адрес возврата в A; когда B вызывает C, в стек заносится адрес возврата в B. Когда C заканчивается, адрес возврата выбирается из вершины стека - а это адрес возврата в B. Когда заканчивается B, в вершине стека находится адрес возврата в A, и возврат из B произойдет в A.
В микропроцессорах семейства Intel, как и в большинстве современных процессорных архитектур, поддерживается аппаратный стек. Аппаратный стек расположен в ОЗУ, указатель стека содержится в паре специальных регистров - SS:SP, доступных для программиста. Аппаратный стек расширяется в сторону уменьшения адресов, указатель его адресует первый свободный элемент. Выполнение команд CALL и INT, а также аппаратных прерываний включает в себя запись в аппаратный стек адреса возврата. Выполнение команд RET и IRET включает в себя выборку из аппаратного стека адреса возврата и передачу управления по этому адресу. Пара команд - PUSH и POP - обеспечивает использование аппаратного стека для программного решения других задач.
Системы программирования для блочно-ориентированных языков (PASCAL, C и др.) используют стек для размещения в нем локальных переменных процедур и иных программных блоков. При каждой активизации процедуры память для ее локальных переменных выделяется в стеке; при завершении процедуры эта память освобождается. Поскольку при вызовах процедур всегда строго соблюдается вложенность, то в вершине стека всегда находится память, содержащая локальные переменные активной в данный момент процедуры.
Этот прием делает возможной легкую реализацию рекурсивных процедур. Когда процедура вызывает сама себя, то для всех ее локальных переменных выделяется новая память в стеке, и вложенный вызов работает с собственным представлением локальных переменных. Когда вложенный вызов завершается, занимаемая его переменными область памяти в стеке освобождается и актуальным становится представление локальных переменных предыдущего уровня. За счет этого в языках PASCAL и C любые процедуры/функции могут вызывать сами себя. В языке PL/1, где по умолчанию приняты другие способы размещения локальных переменных, рекурсивная процедура должна быть определена с описателем RECURSIVE - только тогда ее локальные переменные будут размещаться в стеке.
Рекурсия использует стек в скрытом от программиста виде, но все рекурсивные процедуры могут быть реализованы и без рекурсии, но с явным использованием стека. В программном примере 3.17 приведена реализация быстрой сортировки Хоара в рекурсивной процедуре. Программный пример 4.2 показывает, как будет выглядеть другая реализация того же алгоритма.
{==== Программный пример 4.2 ====}
{ Быстрая сортировка Хоара (стек) }
Procedure Sort(a : Seq); { см. раздел 3.8 }
type board=record { границы обрабатываемого участка }
i0, j0 : integer; end;
Var i0, j0, i, j, x : integer;
flag_j : boolean;
stack : array[1..N] of board; { стек }
stp : integer; { указатель стека работает на увеличение }
begin { в стек заносятся общие границы }
stp:=1; stack[i].i0:=1; stack[i].j0:=N;
while stp>0 do { выбрать границы из стека }
begin i0:=stack[stp].i0; j0:=stack[stp].j0; stp:=stp-1;
i:=i0; j:=j0; flag_j:=false;{проход перестановок от i0 до j0}
while ia[j] then { перестановка }
begin x:=a[i]; a[i]:=a[j]; a[j]:=x; flag_j:= not flag_j;
end;
if flag_j then Dec(j) else Inc(i);
end; if i-1>i0 then {занесение в стек границ левого участка}
begin stp:=stp+1; stack[stp].i0:=i0; stack[stp].j0:=i-1;
end; if j0>i+1 then {занесение в стек границ правого участка}
begin stp:=stp+1; stack[stp].i0:=i+1; stack[stp].j0:=j0;
end; end;
Один проход сортировки Хоара разбивает исходное множество на два множества. Границы полученных множеств запоминаются в стеке. Затем из стека выбираются границы, находящиеся в вершине, и обрабатывается множество, определяемое этими границами. В процессе его обработки в стек может быть записана новая пара границ и т.д. При начальных установках в стек заносятся границы исходного множества. Сортировка заканчивается с опустошением стека.
Очередью FIFO (First - In - First- Out - "первым пришел - первым исключается"). называется такой последовательный список с переменной длиной, в котором включение элементов выполняется только с одной стороны списка (эту сторону часто называют концом или хвостом очереди), а исключение - с другой стороны (называемой началом или головой очереди). Те самые очереди к прилавкам и к кассам, которые мы так не любим, являются типичным бытовым примером очереди FIFO.
Основные операции над очередью - те же, что и над стеком - включение, исключение, определение размера, очистка, неразрушающее чтение.
При представлении очереди вектором в статической памяти в дополнение к обычным для дескриптора вектора параметрам в нем должны находиться два указателя: на начало очереди (на первый элемент в очереди) и на ее конец (первый свободный элемент в очереди). При включении элемента в очередь элемент записывается по адресу, определяемому указателем на конец, после чего этот указатель увеличивается на единицу. При исключении элемента из очереди выбирается элемент, адресуемый указателем на начало, после чего этот указатель уменьшается на единицу.
Очевидно, что со временем указатель на конец при очередном включении элемента достигнет верхней границы той области памяти, которая выделена для очереди. Однако, если операции включения чередовались с операциями исключения элементов, то в начальной части отведенной под очередь памяти имеется свободное место. Для того, чтобы места, занимаемые исключенными элементами, могли быть повторно использованы, очередь замыкается в кольцо: указатели (на начало и на конец), достигнув конца выделенной области памяти, переключаются на ее начало. Такая организация очереди в памяти называется кольцевой очередью. Возможны, конечно, и другие варианты организации: например, всякий раз, когда указатель конца достигнет верхней границы памяти, сдвигать все непустые элементы очереди к началу области памяти, но как этот, так и другие варианты требуют перемещения в памяти элементов очереди и менее эффективны, чем кольцевая очередь.
В исходном состоянии указатели на начало и на конец указывают на начало области памяти. Равенство этих двух указателей (при любом их значении) является признаком пустой очереди. Если в процессе работы с кольцевой очередью число операций включения превышает число операций исключения, то может возникнуть ситуация, в которой указатель конца "догонит" указатель начала. Это ситуация заполненной очереди, но если в этой ситуации указатели сравняются, эта ситуация будет неотличима от ситуации пустой очереди. Для различения этих двух ситуаций к кольцевой очереди предъявляется требование, чтобы между указателем конца и указателем начала оставался "зазор" из свободных элементов. Когда этот "зазор" сокращается до одного элемента, очередь считается заполненной и дальнейшие попытки записи в нее блокируются. Очистка очереди сводится к записи одного и того же (не обязательно начального) значения в оба указателя. Определение размера состоит в вычислении разности указателей с учетом кольцевой природы очереди.
Программный пример 4.3 иллюстрирует организацию очереди и операции на ней.
{==== Программный пример 4.3 ====}
unit Queue; { Очередь FIFO - кольцевая }
Interface
const SIZE=...; { предельный размер очереди }
type data = ...; { эл-ты могут иметь любой тип }
Procesure QInit;
Procedure Qclr;
Function QWrite(a: data) : boolean;
Function QRead(var a: data) : boolean;
Function Qsize : integer;
Implementation { Очередь на кольце }
var QueueA : array[1..SIZE] of data; { данные очереди }
top, bottom : integer; { начало и конец }
Procedure QInit; {** инициализация - начало=конец=1 }
begin top:=1; bottom:=1; end;
Procedure Qclr; {**очистка - начало=конец }
begin top:=bottom; end;
Function QWrite(a : data) : boolean; {** запись в конец }
begin
if bottom mod SIZE+1=top then { очередь полна } QWrite:=false
else begin
{ запись, модификация указ.конца с переходом по кольцу }
Queue[bottom]:=a; bottom:=bottom mod SIZE+1; QWrite:=true;
end; end; { QWrite }
Function QRead(var a: data) : boolean; {** выборка из начала }
begin
if top=bottom then QRead:=false else
{ запись, модификация указ.начала с переходом по кольцу }
begin a:=Queue[top]; top:=top mod SIZE + 1; QRead:=true;
end; end; { QRead }
Function QSize : integer; {** определение размера }
begin
if top <= bottom then QSize:=bottom-top
else QSize:=bottom+SIZE-top;
end; { QSize }
END.
В реальных задачах иногда возникает необходимость в формировании очередей, отличных от FIFO или LIFO. Порядок выборки элементов из таких очередей определяется приоритетами элементов. Приоритет в общем случае может быть представлен числовым значением, которое вычисляется либо на основании значений каких-либо полей элемента, либо на основании внешних факторов. Так, и FIFO, и LIFO-очереди могут трактоваться как приоритетные очереди, в которых приоритет элемента зависит от времени его включения в очередь. При выборке элемента всякий раз выбирается элемент с наибольшим приоритетом.
Очереди с приоритетами могут быть реализованы на линейных списковых структурах - в смежном или связном представлении. Возможны очереди с приоритетным включением - в которых последовательность элементов очереди все время поддерживается упорядоченной, т.е. каждый новый элемент включается на то место в последовательности, которое определяется его приоритетом, а при исключении всегда выбирается элемент из начала. Возможны и очереди с приоритетным исключением - новый элемент включается всегда в конец очереди, а при исключении в очереди ищется (этот поиск может быть только линейным) элемент с максимальным приоритетом и после выборки удаляется из последовательности. И в том, и в другом варианте требуется поиск, а если очередь размещается в статической памяти - еще и перемещение элементов.
Наиболее удобной формой для организации больших очередей с приоритетами является сортировка элементов по убыванию приоритетов частично упорядоченным деревом, рассмотренная нами в п.3.9.2.
Идеальным примером кольцевой очереди в вычислительной системы является буфер клавиатуры в Базовой Системе Ввода-Вывода ПЭВМ IBM PC. Буфер клавиатуры занимает последовательность байтов памяти по адресам от 40:1E до 40:2D включительно. По адресам 40:1A и 40:1C располагаются указатели на начало и конец очереди соответственно. При нажатии на любую клавишу генерируется прерывание 9. Обработчик этого прерывания читает код нажатой клавиши и помещает его в буфер клавиатуры - в конец очереди. Коды нажатых клавиш могут накапливаться в буфере клавиатуры, прежде чем они будут прочитаны программой. Программа при вводе данные с клавиатуры обращается к прерыванию 16H. Обработчик этого прерывания выбирает код клавиши из буфера - из начала очереди - и передает в программу.
Очередь является одним из ключевых понятий в многозадачных операционных системах (Windows NT, Unix, OS/2, ЕС и др.). Ресурсы вычислительной системы (процессор, оперативная память, внешние устройства и т.п.( используются всеми задачами, одновременно выполняемыми в среде такой операционной системы. Поскольку многие виды ресурсов не допускают реально одновременного использования разными задачами, такие ресурсы предоставляются задачам поочередно. Таким образом, задачи, претендующие на использование того или иного ресурса, выстраиваются в очередь к этому ресурсу. Эти очереди обычно приоритетные, однако, довольно часто применяются и FIFO-очереди, так как это единственная логическая организация очереди, которая гарантированно не допускает постоянного вытеснения задачи более приоритетными. LIFO-очереди обычно используются операционными системами для учета свободных ресурсов.
Также в современных операционных системах одним из средств взаимодействия между параллельно выполняемыми задачами являются очереди сообщений, называемые также почтовыми ящиками. Каждая задача имеет свою очередь - почтовый ящик, и все сообщения, отправляемые ей от других задач, попадают в эту очередь. Задача-владелец очереди выбирает из нее сообщения, причем может управлять порядком выборки - FIFO, LIFO или по приоритету.
Дек - особый вид очереди. Дек (от англ. deq - double ended queue,т.е очередь с двумя концами) - это такой последовательный список, в котором как включение, так и исключение элементов может осуществляться с любого из двух концов списка. Частный случай дека - дек с ограниченным входом и дек с ограниченным выходом. Логическая и физическая структуры дека аналогичны логической и физической структуре кольцевой FIFO-очереди. Однако, применительно к деку целесообразно говорить не о начале и конце, а о левом и правом конце.
Операции над деком:
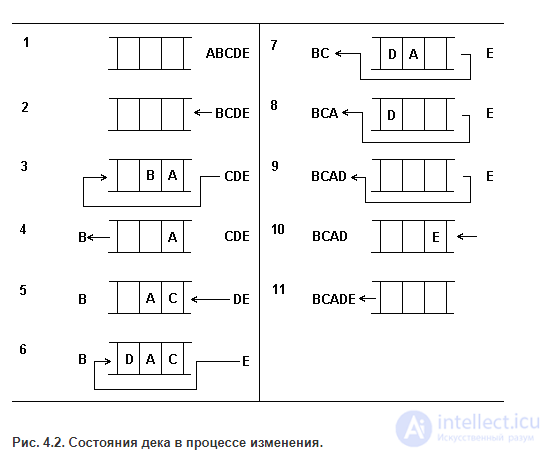
Рис. 4.2. Состояния дека в процессе изменения.
На рис. 4.2 в качестве примера показана последовательность состояний дека при включении и удалении пяти элементов. На каждом этапе стрелка указывает с какого конца дека (левого или правого) осуществляется включение или исключение элемента. Элементы соответственно обозначены буквами A, B, C, D, E.
Физическая структура дека в статической памяти идентична структуре кольцевой очереди. Разработать программный пример, иллюстрирующий организацию дека и операции над ним не сложно по образцу примеров 4.1, 4.3. В этом модуле должны быть реализованы процедуры и функции:
Function DeqWrRight(a: data): boolean; - включение элемента справа;
Function DeqWrLeft(a: data): boolean; - включение элемента слева;
Function DeqRdRight(var a: data): boolean; - исключение элемента справа;
Function DeqRdLeft(var a: data) : boolean; - исключение элемента слева; Procedure DeqClr; - очистка;
Function DeqSize : integer; - определение размера.
Задачи, требующие структуры дека, встречаются в вычислительной технике и программировании гораздо реже, чем задачи, реализуемые на структуре стека или очереди. Как правило, вся организация дека выполняется программистом без каких-либо специальных средств системной поддержки.
Однако, в качестве примера такой системной поддержки рассмотрим организацию буфера ввода в языке REXX. В обычном режиме буфер ввода связан с клавиатурой и работает как FIFO-очередь. Однако, в REXX имеется возможность назначить в качестве буфера ввода программный буфер и направить в него вывод программ и системных утилит. В распоряжении программиста имеются операции QUEUE - запись строки в конец буфера и PULL - выборка строки из начала буфера. Дополнительная операция PUSH - запись строки в начало буфера - превращает буфер в дек с ограниченным выходом. Такая структура буфера ввода позволяет программировать на REXX весьма гибкую конвейерную обработку с направлением выхода одной программы на вход другой и модификацией перенаправляемого потока.
Строка - это линейно упорядоченная последовательность символов, принадлежащих конечному множеству символов, называемому алфавитом.
Строки обладают следующими важными свойствами:
Говоря о строках, обычно имеют в виду текстовые строки - строки, состоящие из символов, входящих в алфавит какого-либо выбранного языка, цифр, знаков препинания и других служебных символов. Действительно, текстовая строка является наиболее универсальной формой представления любой информации: на сегодняшний день вся сумма информации, накопленной человечеством - от Ветхого Завета до нашего учебного пособия - представлена именно в виде текстовых строк. В наших дальнейших примерах этого раздела будем работать именно с текстовыми строками. Однако, следует иметь в виду, что символы, входящие в строку могут принадлежать любому алфавиту. Так, в языке PL/1, наряду с типом данных "символьная строка" - CHAR(n) - существует тип данных "битовая строка" - BIT(n). Битовые строки, составляются из 1-битовых символов, принадлежащих алфавиту: { 0, 1 }. Все строковые операции с равным успехом применимы как к символьным, так и к битовым строкам.
Кодирование символов было рассмотрено в главе 2. Отметим, что в зависимости от особенности задачи, свойств применяемого алфавита и представляемого им языка и свойств носителей информации могут применяться и другие способы кодирования символов. В современных вычислительных системах, однако, повсеместно принята кодировка всего множества символов на разрядной сетке фиксированного размера (1 байт).
Хотя строки рассматриваются в главе, посвященной полустатическим структурам данных, в тех или иных конкретных задачах изменчивость строк может варьироваться от полного ее отсутствия до практически неограниченных возможностей изменения. Ориентация на ту или иную степень изменчивости строк определяет и физическое представление их в памяти и особенности выполнения операций над ними. В большинстве языков программирования (C, PASCASL, PL/1 и др.) строки представляются именно как полустатические структуры.
В зависимости от ориентации языка программирования средства работы со строками занимают в языке более или менее значительное место. Рассмотрим три примера возможностей работы со строками.
Язык C является языком системного программирования, типы данных, с которыми работает язык C, максимально приближены к тем типам, с которыми работают машинные команды. Поскольку машинные команды не работают со строками, нет такого типа данных и в языке C. Строки в C представляются в виде массивов символов. Операции над строками могут быть выполнены как операции обработки массивов или же при помощи библиотечных (но не встроенных!) функций строковой обработки.
В языках универсального назначения обычно строковый тип является базовым в языке: STRING в PASCAL, CHAR(n) в PL/1. (В PASCAL длина строки, объявленной таким образом, может меняться от 0 до n, в PL/1 чтобы длина строки могла меняться, она должна быть объявлена с описателем VARING.) Основные операции над строками реализованы как простые операции или встроенные функции. Возможны также библиотеки, обеспечивающие расширенный набор строковых операций.
Язык REXX ориентирован прежде всего на обработку текстовой информации. Поэтому в REXX нет средств описания типов данных: все данные представляются в виде символьных строк. Операции над данными, не свойственные символьным строкам, либо выполняются специальными функциями, либо приводят к прозрачному для программиста преобразованию типов. Так, например, интерпретатор REXX, встретив оператор, содержащий арифметическое выражение, сам переводит его операнды в числовой тип, вычисляет выражение и преобразует результат в символьную строку. Целый ряд строковых операций является простыми операциями языка, а встроенных функций обработки строк в REXX несколько десятков.
Базовыми операциями над строками являются:
Операция определения длины строки имеет вид функции, возвращаемое значение которой - целое число - текущее число символов в строке. Операция присваивания имеет тот же смысл, что и для других типов данных.
Операция сравнения строк имеет тот же смысл, что и для других типов данных. Сравнение строк производится по следующим правилам. Сравниваются первые символы двух строк. Если символы не равны, то строка, содержащая символ, место которого в алфавите ближе к началу, считается меньшей. Если символы равны, сравниваются вторые, третьи и т.д. символы. При достижении одной конца одной из строк строка меньшей длины считается меньшей. При равенстве длин строк и попарном равенстве всех символов в них строки считаются равными.
Результатом операции сцепления двух строк является строка, длина которой равна суммарной длине строк-операндов, а значение соответствует значению первого операнда, за которым непосредственно следует значение второго операнда. Операция сцепления дает результат, длина которого в общем случае больше длин операндов. Как и во всех операциях над строками, которые могут увеличивать длину строки (присваивание, сцепление, сложные операции), возможен случай, когда длина результата окажется большей, чем отведенный для него объем памяти. Естественно, эта проблема возникает только в тех языках, где длина строки ограничивается. Возможны три варианта решения этой проблемы, определяемые правилами языка или режимами компиляции:
Операция выделения подстроки выделяет из исходной строки последовательность символов, начиная с заданной позиции n, с заданной длиной l. В языке PASCAL соответствующая функция называется COPY. В языках PL/1, REXX соответствующая функция - SUBSTR - обладает интересным свойством, отсутствующим в PASCAL. Функция SUBSTR может употребляться в левой части оператора присваивания. Например, если исходное значение некоторой строки S - 'ABCDEFG', то выполнение оператора: SUBSTR(S,3,3)='012'; изменит значение строки S на - 'AB012FG'.
При реализации операции выделения подстроки в языке программирования и в пользовательской процедуре обязательно должно быть определено правило получения результата для случая, когда начальная позиция n задана такой, что оставшаяся за ней часть исходной строки имеет длину, меньшую заданной длины l, или даже n превышает длину исходной строки. Возможные варианты такого правила:
Операция поиска вхождения находит место первого вхождения подстроки-эталона в исходную строку. Результатом операции может быть номер позиции в исходной строке, с которой начинается вхождение эталона или указатель на начало вхождения. В случае отсутствия вхождения результатом операции должно быть некоторое специальное значение, например, нулевой номер позиции или пустой указатель.
На основе базовых операций могут быть реализованы и любые другие, даже сложные операции над строками. Например, операция удаления из строки символов с номерами от n1 включительно n2 может быть реализована как последовательность следующих шагов:
Впрочем, в целях повышения эффективности некоторые вторичные операции также могут быть реализованы как базовые - по собственным алгоритмам, с непосредственным доступом к физической структуре строки.
Представление строк в памяти зависит от того, насколько изменчивыми являются строки в каждой конкретной задаче, и средства такого представления варьируются от абсолютно статического до динамического. Универсальные языки программирования в основном обеспечивают работу со строками переменной длины, но максимальная длина строки должна быть указана при ее создании. Если программиста не устраивают возможности или эффективность тех средств работы со строками, которые предоставляет ему язык программирования, то он может либо определить свой тип данных "строка" и использовать для его представления средства динамической работы с памятью, либо сменить язык программирования на специально ориентированный на обработку текста (CNOBOL, REXX), в которых представление строк базируется на динамическом управлении памятью.
ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ СТРОК.
Представление строк в виде векторов, принятое в большинстве универсальных языков программирования, позволяет работать со строками, размещенными в статической памяти. Кроме того, векторное представление позволяет легко обращаться к отдельным символам строки как к элементам вектора - по индексу.
Самым простым способом является представление строки в виде вектора постоянной длинны. При этом в памяти отводится фиксированное количество байт, в которые записываются символы строки. Если строка меньше отводимого под нее вектора, то лишние места заполняются пробелами, а если строка выходит за пределы вектора, то лишние (обычно справа строки) символы должны быть отброшены.
На рис.4.3 приведена схема, на которой показано представление двух строк: 'ABCD' и 'PQRSTUVW' в виде вектора постоянной длины на шесть символов.

Рис. 4.3. Представление строк векторами постоянной длины
ПРЕДСТАВЛЕНИЕ СТРОК ВЕКТОРОМ ПЕРЕМЕННОЙ ДЛИНЫ С ПРИЗНАКОМ КОНЦА.
Этот и все последующие за ним методы учитывают переменную длину строк. Признак конца - это особый символ, принадлежащий алфавиту (таким образом, полезный алфавит оказывается меньше на один символ), и занимает то же количество разрядов, что и все остальные символы. Издержки памяти при этом способе составляют 1 символ на строку. Такое представление строки показано на рис.4.4. Специальный символ-маркер конца строки обозначен здесь 'eos'. В языке C, например, в качестве маркера конца строки используется символ с кодом 0.

Рис. 4.4. Представление строк переменной длины с признаком конца
ПРЕДСТАВЛЕНИЕ СТРОК ВЕКТОРОМ ПЕРЕМЕННОЙ ДЛИНЫ СО СЧЕТЧИКОМ.
Счетчик символов - это целое число, и для него отводится достаточное количество битов, чтобы их с избытком хватало для представления длины самой длинной строки,какую только можно представить в данной машине. Обычно для счетчика отводят от 8 до 16 битов. Тогда при таком представлении издержки памяти в расчете на одну строку составляют 1-2 символа. При использовании счетчика символов возможен произвольный доступ к символам в пределах строки, поскольку можно легко проверить, что обращение не выходит за пределы строки. Счетчик размещается в таком месте, где он может быть легко доступен - начале строки или в дескрипторе строки. Максимально возможная длина строки, таким образом, ограничена разрядностью счетчика. В PASCAL, например, строка представляется в виде массива символов, индексация в котором начинается с 0; однобайтный счетчик числа символов в строке является нулевым элементом этого массива. Такое представление строк показано на рис.4.5. И счетчик символов, и признак конца в предыдущем случае могут быть доступны для программиста как элементы вектора.

Рис.4.5. Представление строк переменной длины со счетчиком
В двух предыдущих вариантах обеспечивалось максимально эффективное расходование памяти (1-2 "лишних" символа на строку), но изменчивость строки обеспечивалась крайне неэффективно. Поскольку вектор - статическая структура, каждое изменение длины строки требует создания нового вектора, пересылки в него неизменяемой части строки и уничтожения старого вектора. Это сводит на нет все преимущества работы со статической памятью. Поэтому наиболее популярным способом представления строк в памяти являются вектора с управляемой длиной.
ВЕКТОР С УПРАВЛЯЕМОЙ ДЛИНОЙ.
Память под вектор с управляемой длиной отводится при создании строки и ее размер и размещение остаются неизменными все время существования строки. В дескрипторе такого вектора-строки может отсутствовать начальный индекс, так как он может быть зафиксирован раз навсегда установленными соглашениями, но появляется поле текущей длины строки. Размер строки, таким образом, может изменяться от 0 до значения максимального индекса вектора. "Лишняя" часть отводимой памяти может быть заполнена любыми кодами - она не принимается во внимание при оперировании со строкой. Поле конечного индекса может быть использовано для контроля превышения длиной строки объема отведенной памяти. Представление строк в виде вектора с управляемой длиной (при максимальной длине 10) показано на рис.4.6.
Хотя такое представление строк не обеспечивает экономии памяти, проектировщики систем программирования, как видно, считают это приемлемой платой за возможность работать с изменчивыми строками в статической памяти.
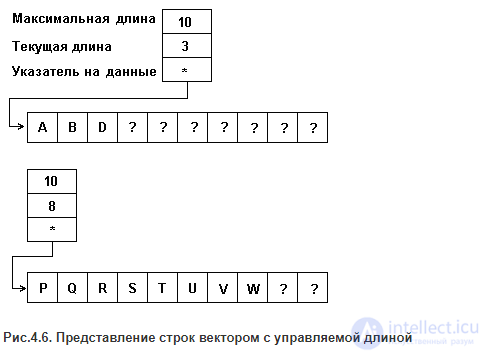
Рис.4.6. Представление строк вектором с управляемой длиной
В программном примере 4.4 приведен модуль, реализующий представление строк вектором с управляемой длиной и некоторые операции над такими строками. Для уменьшения объема в примере в секции Implementation определены не все процедуры/функции. Предоставляем читателю самостоятельно разработать прочие объявленные в секции Interface подпрограммы. Дескриптор строки описывается типом _strdescr, который в точности повторяет структуру, показанную на рис.4.6. Функция NewStr выделяет две области памяти: для дескриптора строки и для области данных строки. Адрес дескриптора строки, возвращаемый функцией NewStr - тип varstr - является той переменной, значение которой указывается пользователем модуля для идентификации конкретной строки при всех последующих операциях с нею. Область данных, указатель на которую заносится в дескрипторе строки - тип _dat_area - описана как массив символов максимального возможного объема - 64 Кбайт. Однако, объем памяти, выделяемый под область данных функцией NewStr, как правило, меньший - он задается параметром функции. Хотя индексы в массиве символов строки теоретически могут изменяться от 1 до 65535, значение индекса в каждой конкретной строке при ее обработке ограничивается полем maxlen дескриптора данной строки. Все процедуры/функции обработки строк работают с символами строки как с элементами вектора, обращаясь к ним по индексу. Адрес вектора процедуры получают из дескриптора строки. Обратите внимание на то, что в процедуре CopyStr длина результата ограничивается максимальной длиной целевой строки.
{==== Программный пример 4.4 ====}
{ Представление строк вектором с управляемой длиной }
Unit Vstr;
Interface
type _dat_area = array[1..65535] of char;
type _strdescr = record { дескриптор строки }
maxlen, curlen : word; { максимальная и текущая длины }
strdata : ^_dat_area; { указатель на данные строки }
end;
type varstr = ^_strdescr; { тип - СТРОКА ПЕРЕМЕННОЙ ДЛИНЫ }
Function NewStr(len : word) : varstr;
Procedure DispStr(s : varstr);
Function LenStr(s : varstr) : word;
Procedure CopyStr(s1, s2 : varstr);
Function CompStr(s1, s2 : varstr) : integer;
Function PosStr(s1, s2 : varstr) : word;
Procedure ConcatStr(var s1: varstr; s2 : varstr);
Procedure SubStr(var s1 : varstr; n, l : word);
Implementation
{** Создание строки; len - максимальная длина строки;
ф-ция возвращает указатель на дескриптор строки }
Function NewStr(len : word) : varstr;
var addr : varstr;
daddr : pointer;
begin
New(addr); { выделение памяти для дескриптора }
Getmem(daddr,len); { выделение памяти для данных }
{ занесение в дескриптор начальных значений }
addr^.strdata:=daddr; addr^.maxlen:=len; addr^.curlen:=0;
Newstr:=addr;
end; { Function NewStr }
Procedure DispStr(s : varstr); {** Уничтожение строки }
begin
FreeMem(s^.strdata,s^.maxlen); { уничтожение данных }
Dispose(s); { уничтожение дескриптора }
end; { Procedure DispStr }
{** Определение длины строки, длина выбирается из дескриптора }
Function LenStr(s : varstr) : word;
begin
LenStr:=s^.curlen;
end; { Function LenStr }
Procedure CopyStr(s1, s2 : varstr); { Присваивание строк s1:=s2}
var i, len : word;
begin
{ длина строки-результата м.б. ограничена ее макс. длиной }
if s1^.maxlen s2; -1 - если s1 < s2 }
Function CompStr(s1, s2 : varstr) : integer;
var i : integer;
begin i:=1; { индекс текущего символа }
{ цикл, пока не будет достигнут конец одной из строк }
while (i <= s1^.curlen) and (i <= s2^.curlen) do
{ если i-ые символы не равны, функция заканчивается }
begin if s1^.strdata^[i] > s2^.strdata^[i] then
begin CompStr:=1; Exit; end;
if s1^.strdata^[i] < s2^.strdata^[i] then
begin CompStr:=-1; Exit; end;
i:=i+1; { переход к следующему символу }
end;
{ если выполнение дошло до этой точки, то найден конец одной из строк, и все сравненные до сих пор символы были равны; строка меньшей длины считается меньшей }
if s1^.curlens2^.curlen then CompStr:=1
else CompStr:=0;
end; { Function CompStr }
.
.
END.
СИМВОЛЬНО - СВЯЗНОЕ ПРЕДСТАВЛЕНИЕ СТРОК.
Списковое представление строк в памяти обеспечивает гибкость в выполнении разнообразных операций над строками (в частности, операций включения и исключения отдельных символов и целых цепочек) и использование системных средств управления памятью при выделении необходимого объема памяти для строки. Однако, при этом возникают дополнительные расходы памяти. Другим недостатком спискового представления строки является то, что логически соседние элементы строки не являются физически соседними в памяти. Это усложняет доступ к группам элементов строки по сравнению с доступом в векторном представлении строки.
ОДНОНАПРАВЛЕННЫЙ ЛИНЕЙНЫЙ СПИСОК.
Каждый символ строки представляется в виде элемента связного списка; элемент содержит код символа и указатель на следующий элемент, как показано на рис.4.7. Одностороннее сцепление представляет доступ только в одном направлении вдоль строки. На каждый символ строки необходим один указатель, который обычно занимает 2-4 байта.
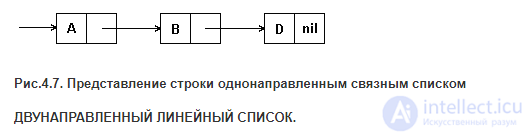
Рис.4.7. Представление строки однонаправленным связным списком
ДВУНАПРАВЛЕННЫЙ ЛИНЕЙНЫЙ СПИСОК.
В каждый элемент списка добавляется также указатель на предыдущий элемент, как показано на рис.4.8. Двустороннее сцепление допускает двустороннее движение вдоль списка, что может значительно повысить эффективность выполнения некоторых строковых операция. При этом на каждый символ строки необходимо два указателя , т.е. 4-8 байт.
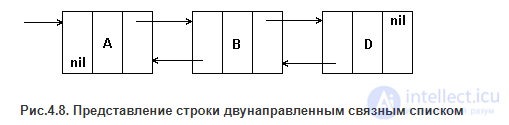
Рис.4.8. Представление строки двунаправленным связным списком
БЛОЧНО - СВЯЗНОЕ ПРЕДСТАВЛЕНИЕ СТРОК.
Это представление позволяет в болшинстве операций избежать затрат, связанных с управлением динамической памятью, но в то же время обеспечивает достаточно эффективное использование памяти при работе со строками переменной длины.
МНОГОСИМВОЛЬНЫЕ ЗВЕНЬЯ ФИКСИРОВАННОЙ ДЛИНЫ.
Многосимвольные группы (звенья) организуются в список, так что каждый элемент списка, кроме последнего, содержит группу элементов строки и указатель следующего элемента списка. Поле указателя последнего элемента списка хранит признак конца - пустой указатель. В процессе обработки строки из любой ее позиции могут быть исключены или в любом месте вставлены элементы, в результате чего звенья могут содержать меньшее число элементов, чем было первоначально. По этой причине необходим специальный символ, который означал бы отсутствие элемента в соответствующей позиции строки. Обозначим такой символ 'emp', он не должен входить в множество символов,из которых организуется строка. Пример многосимвольных звеньев фиксированной длинны по 4 символа в звене показан на рис.4.9.
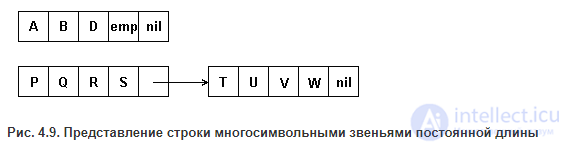
Рис. 4.9. Представление строки многосимвольными звеньями постоянной длины
Такое представление обеспечивает более эффективное использование памяти, чем символьно-связное. Операции вставки/удаления в ряде случаев могут сводиться к вставке/удалению целых блоков. Однако, при удалении одиночных символов в блоках могут накапливаться пустые символы emp, что может привести даже к худшему использованию памяти, чем в символьно-связном представлении.
МНОГОСИМВОЛЬНЫЕ ЗВЕНЬЯ ПЕРЕМЕННОЙ ДЛИНЫ.
Переменная длинна блока дает возможность избавиться от пустых символов и тем самым экономить память для строки. Однако появляется потребность в специальном символе - признаке указателя, на рис.4.10 он обозначен символом 'ptr'.
С увеличением длины групп символом, хранящихся в блоках, эффективность использования памяти повышается. Однако негативной характеристикой рассматриваемого метода является усложнение операций по резервированию памяти для элементов списка и возврату освободившихся элементов в общий список доступной памяти.
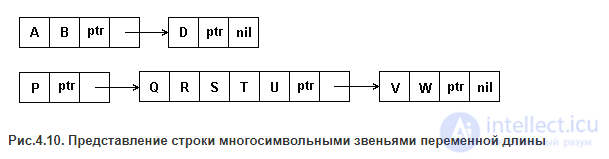
Рис.4.10. Представление строки многосимвольными звеньями переменной длины
Такой метод спискового представления строк особенно удобен в задачах редактирования текста, когда большая часть операций приходится на изменение, вставку и удаление целых слов. Поэтому в этих задачах целесообразно список организовать так, чтобы каждый его элемент содержал одно слово текста. Символы пробела между словами в памяти могут не представляются.
МНОГОСИМВОЛЬНЫЕ ЗВЕНЬЯ С УПРАВЛЯЕМОЙ ДЛИНОЙ.
Память выделяется блоками фиксированной длины. В каждом блоке помимо символов строки и указателя на следующий блок содержится номера первого и последнего символов в блоке. При обработке строки в каждом блоке обрабатываются только символы, расположенные между этими номерами. Признак пустого символа не используется: при удалении символа из строки оставшиеся в блоке символы уплотняются и корректируются граничные номера. Вставка символа может быть выполнена за счет имеющегося в блоке свободного места, а при отсутствии такового - выделением нового блока. Хотя операции вставки/удаления требуют пересылки символов, диапазон пересылок ограничивается одним блоком. При каждой операции изменения может быть проанализирована заполненность соседних блоков и два полупустых соседних блока могут быть переформированы в один блок. Для определения конца строки может использоваться как пустой указатель в последнем блоке, так и указатель на последний блок в дескрипторе строки. Последнее может быть весьма полезным при выполнении некоторых операций, например, сцепления. В дескрипторе может храниться также и длина строки: считывать ее из дескриптора удобнее, чем подсчитывать ее перебором всех блоков строки.
Пример представления строки в виде звеньев с управляемой длиной 8 показан на рис.4.11.
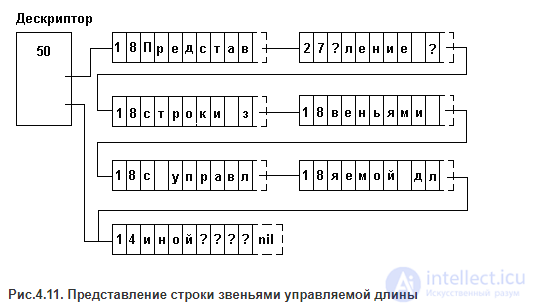
Рис.4.11. Представление строки звеньями управляемой длины
В программном примере 4.5 приведен модуль, реализующий представление строк звеньями с управляемой длиной. Даже с первого взгляда видно, что он значительно сложнее, чем пример 4.4. Это объясняется тем, что здесь вынуждены обрабатывать как связные (списки блоков), так и векторные (массив символов в каждом блоке) структуры. Поэтому при последовательной обработке символов строки процедура должна сохранять как адрес текущего блока, так и номер текущего символа в блоке. Для этих целей во всех процедурах/функциях используются переменные cp и bi соответственно. (Процедуры и функции, обрабатывающие две строки - cp1, bi1, cp2, bi2.) Дескриптор строки - тип _strdescr - и блок - тип _block - в точности повторяют структуру, показанную на рис.4.10. Функция NewStr выделяет память только для дескриптора строки и возвращает адрес дескриптора - тип varstr - он служит идентификатором строки при последующих операциях с нею. Память для хранения данных строки выделяется только по мере необходимости. Во всех процедурах/функциях приняты такие правила работы с памятью:
Для освобождения блоков определена специальная внутренняя функция FreeBlock, освобождающая весь список блоков, голова которого задается ее параметром.
Обратите внимание на то, что ни в каких процедурах не контролируется максимальный объем строки результата - он может быть сколь угодно большим, а поле длины в дескрипторе строки имеет тип longint.
{==== Программный пример 4.5 ====}
{ Представление строки звеньями управляемой длины }
Unit Vstr;
Interface
const BLKSIZE = 8; { число символов в блоке }
type _bptr = ^_block; { указатель на блок }
_block = record { блок }
i1, i2 : byte; { номера 1-го и последнего символов }
strdata : array [1..BLKSIZE] of char; { символы }
next : _bptr; { указатель на следующий блок }
end;
type _strdescr = record { дескриптор строки }
len : longint; { длина строки }
first, last : _bptr; { указ.на 1-й и последний блоки }
end;
type varstr = ^_strdescr; { тип - СТРОКА ПЕРЕМЕННОЙ ДЛИНЫ }
Function NewStr : varstr;
Procedure DispStr(s : varstr);
Function LenStr(s : varstr) : longint;
Procedure CopyStr(s1, s2 : varstr);
Function CompStr(s1, s2 : varstr) : integer;
Function PosStr(s1, s2 : varstr) : word;
Procedure ConcatStr(var s1: varstr; s2 : varstr);
Procedure SubStr(var s : varstr; n, l : word);
Implementation
Function NewBlock :_bptr; {Внутр.функция-выделение нового блока}
var n : _bptr;
i : integer;
begin
New(n); { выделение памяти }
n^.next:=nil; n^.i1:=0; n^.i2:=0; { начальные значения }
NewBlock:=n;
end; { NewBlock }
{*** Внутр.функция - освобождение цепочки блока, начиная с c }
Function FreeBlock(c : _bptr) : _bptr;
var x : _bptr;
begin { движение по цепочке с освобождением памяти }
while c<>nil do begin x:=c; c:=c^.next; Dispose(x); end;
FreeBlock:=nil; { всегда возвращает nil }
end; { FreeBlock }
Function NewStr : varstr; {** Создание строки }
var addr : varstr;
begin
New(addr); { выделение памяти для дескриптора }
{ занесение в дескриптор начальных значений }
addr^.len:=0; addr^.first:=nil; addr^.last:=nil;
Newstr:=addr;
end; { Function NewStr }
Procedure DispStr(s : varstr); {** Уничтожение строки }
begin
s^.first:=FreeBlock(s^.first); { уничтожение блоков }
Dispose(s); { уничтожение дескриптора }
end; { Procedure DispStr }
{** Определение длины строки, длина выбирается из дескриптора }
Function LenStr(s : varstr) : longint;
begin
LenStr:=s^.len;
end; { Function LenStr }
{** Присваивание строк s1:=s2 }
Procedure CopyStr(s1, s2 : varstr);
var bi1, bi2 : word; { индексы символов в блоках для s1 и s2 }
cp1, cp2 : _bptr; { адреса текущих блоков для s1 и s2 }
pp : _bptr; { адрес предыдущего блока для s1 }
begin
cp1:=s1^.first; pp:=nil; cp2:=s2^.first;
if s2^.len=0 then begin
{ если s2 пустая, освобождается вся s1 }
s1^.first:=FreeBlock(s1^.first); s1^.last:=nil;
end
else begin
while cp2<>nil do begin { перебор блоков s2 }
if cp1=nil then begin { если в s1 больше нет блоков }
{ выделяется новый блок для s1 }
cp1:=NewBlock;
if s1^.first=nil then s1^.first:=cp1
else if pp<>nil then pp^.next:=cp1;
end;
cp1^:=cp2^; { копирование блока }
{ к следующему блоку }
pp:=cp1; cp1:=cp1^.next; cp2:=cp2^.next;
end; { while }
s1^.last:=pp; { последний блок }
{ если в s1 остались лишние блоки - освободить их }
pp^.next:=FreeBlock(pp^.next);
end; { else }
s1^.len:=s2^.len;
end; { Procedure CopyStr }
{** Сравнение строк - возвращает:
0, если s1=s2; 1 - если s1 > s2; -1 - если s1 < s2 }
Function CompStr(s1, s2 : varstr) : integer;
var bi1, bi2 : word;
cp1, cp2 : _bptr;
begin
cp1:=s1^.first; cp2:=s2^.first;
bi1:=cp1^.i1; bi2:=cp2^.i1;
{ цикл, пока не будет достигнут конец одной из строк }
while (cp1<>nil) and (cp2<>nil) do begin
{ если соответств.символы не равны, ф-ция заканчивается }
if cp1^.strdata[bi1] > cp2^.strdata[bi2] then begin
CompStr:=1; Exit;
end;
if cp1^.strdata[bi1] < cp2^.strdata[bi2] then begin
CompStr:=-1; Exit;
end;
bi1:=bi1+1; { к следующему символу в s1 }
if bi1 > cp1^.i2 then begin cp1:=cp1^.next; bi1:=cp1^.i1; end;
bi2:=bi2+1; { к следующему символу в s2 }
if bi2 > cp2^.i2 then begin cp2:=cp2^.next; bi2:=cp2^.i1; end;
end;
{ мы дошли до конца одной из строк,
строка меньшей длины считается меньшей }
if s1^.len < s2^.len then CompStr:=-1
else if s1^.len > s2^.len then CompStr:=1
else CompStr:=0;
end; { Function CompStr }
.
.
END.
Чтобы не перегружать программный пример, в него не включены средства повышения эффективности работы с памятью. Такие средства включаются в операции по выбору программиста. Обратите внимание, например, что в процедуре, связанной с копированием данных (CopyStr) у нас копируются сразу целые блоки. Если в блоке исходной строки были неиспользуемые места, то они будут и в блоке результирующей строки. Посимвольное копирование позволило бы устранить избыток памяти в строке-результате. Оптимизация памяти, занимаемой данными строки может производится как слиянием соседних полупустых блоков, так и полным уплотнением данных. В дескриптор строки может быть введено поле - количество блоков в строке. Зная общее количество блоков и длину строки можно при выполнении неко- торых операций оценивать потери памяти и выполнять уплотнение, если эти потери превосходят какой-то установленный процент.
На этом все! Теперь вы знаете все про полустатические структуры данных, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое полустатические структуры данных, реализация строк, стеки и очереди и строки и деки и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных