1.Типы данных, виды. классификация, примеры

Привет, сегодня поговорим про типы данных, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое типы данных , настоятельно рекомендую прочитать все из категории Структуры данных.

Введение

Компьютер - это машина, которая обрабатывает информацию. Изучение компьютерных наук предполагает изучение того, каким образом эта информация организована внутри компьютера, как она обрабатывается и как может быть использована. Следовательно, для изучения предмета студенту особенно важно понять концепции организации информации и работы с ней.

Так как вычислительная техника базируется на изучении информации, то первый возникающий вопрос заключается в том, что такое информация. К сожалению, несмотря на то , что концепция информации является краеугольным камнем всей науки о вычислительной технике, на этот вопрос не может быть дано однозначного ответа. В этом контексте понятие "информация" в вычислительной технике сходно с понятием "точка", "прямая" и "плоскость" в геометрии - все это неопределенные термины, о которых могут быть сделаны некоторые утверждения и выводы, но которые не могут быть объяснены в терминах более элементарных понятий.

Базовой единицей информации является бит, который может принимать два взаимоисключающих значения. Если устройство может находиться более чем в двух состояниях, то тот факт, что оно находится в одном из этих состояний, уже требует нескольких битов информации.

Для представления двух возможных состояний некоторого бита используются двоичные цифры - нуль и единица.

Число битов, необходимых для кодирования символа в конкретной вычислительной машине, называется размером байта, а группа битов в этом числе называется байтом. Размер байта в большинстве компьютеров равен 8.

Память вычислительной машины представляет собой совокупность битов. в любой момент функционирования в ЭВМ каждый из битов памяти имеет значение 0 или 1 (сброшен или установлен). Состояние бита называется его значением или содержимым.

Биты в памяти ЭВМ группируются в элементы большего размера, например в байты. В некоторых ЭВМ несколько байтов объединяются в группы, называемые словами. Каждому такому элементу назначается адрес, который представляет собой имя, идентифицирующее конкретный элемент памяти среди аналогичных элементов. Этот адрес обычно числовой. Он называется ячейкой, а содержимое ячейки есть значение битов, которые ее составляют.

Итак, мы видим, что информация в ЭВМ сама по себе не имеет конкретного смысла. С некоторой конкретной битовой комбинацией может быть связано любое смысловое значение. Именно интерпретация битовой комбинации придает ей заданный смысл.

Метод интерпретации битовой информации часто называется типом данных. Каждая ЭВМ имеет свой набор типов данных.

Важно осознавать роль, выполняемую спецификацией типа в языках высокого уровня. Именно посредством подобных объявлений программист указывает на то, каким образом содержимое памяти ЭВМ интерпретируется программой. Эти объявления детерминируют объем памяти, необходимый для размещения отдельных элементов, способ интерпретации этих элементов и другие важные детали. Объявления также сообщают интерпретатору точное значение используемых символов операций.

часть 1. введение в теорию структур данных и алгоритмов их обработки

1. типы данных

В математике принято классифицировать переменные в соответствие с некоторыми важными характеристиками. Мы различаем вещественные, комплексные и логические переменные ,переменные ,представляющие собой отдельные значения, множества значений или множества множеств. В обработке данных понятие классификации играет такую же, если не большую роль. Мы будем придерживаться того принципа, что любая константа, переменная, выражение или функция относятся к некоторому типу.

Фактически тип характеризует множество значений, которые может принимать некоторая переменная или выражение и которые может формировать функция.

В информатике тип данных или просто тип представляет собой классификацию информационных сущностей (например, таких как значения или выражения ), определяющую возможность их использования в рамках заданной формальной системы. Понятие имеет несколько определений, которые могут частично пересекаться или приводить к тождественному содержанию. Наиболее принципиально различимых, хотя и не противоречащих друг другу, определений два:

• декларативное — тип есть множество допустимых значений , которые могут принимать данные, принадлежащие к этому типу;
• процедурное — тип определяется поведением, т.е. набором действий, которые можно осуществлять над данными, принадлежащими к этому типу.

Декларативное определение чаще всего используется в императивном программировании, процедурное — в параметрическом полиморфизме. Объектно-ориентированное программирование использует процедурное определение при описании взаимодействия компонентов программы, и декларативное — при описании реализации этих компонентов на ЭВМ, соответственно, рассматривая « класс -как-поведение» и «класс-как- объект в памяти».

Операция назначения типа информационным сущностям называется типизацией. Назначение и проверка согласования типов может осуществляться заранее (статическая типизация), непосредственно при использовании (динамическая типизация) или совмещать оба метода. Типы могут назначаться «раз и навсегда» (сильная типизация) или позволять себя изменять (слабая типизация) — см. сильная и слабая типизация.

Теория типов формально изучает типы и результаты от их назначения. Неотъемлемой частью большинства языков программирования являются системы типов, использующие типы для обеспечения той или иной степени типобезопасности . Лишь немногие языки могут считаться типизированными в полной мере, большинство языков предоставляет лишь некоторый уровень типизированности.

Понятие типобезопасности опирается преимущественно на процедурное определение типа. Например, попытка деления «числа» на «строку» будет отвергнута большинством языков, так как для этих типов не определено соответствующее поведение. Слабо типизированные языки тяготеют к декларативному определению. Например, «число» и «запись» имеют различное поведение, но значение адреса «записи» в памяти ЭВМ может иметь то же низкоуровневое представление, что и «число». Слабо типизированные языки предоставляют возможность нарушить[en] систему типов, назначив этому значению поведение «числа» посредством операцииприведения типа. Подобные трюки могут использоваться для повышения эффективности программ, но несут в себе риск крахов , и поэтому не допускаются вбезопасных языках.

К не полным по Тьюрингу языкам описания данных (таким как SGML) процедурное определение не применимо.

Единообразная обработка данных разных типов называется полиморфизмом.

Классификация типов днных

Существуют различные классификации типов и правил их назначения.

Например, типы делятся на примитивные и агрегатные (последние также называются составными, композитными или структурными). Примерами примитивных типовслужат вещественные, целое, логическое и др. Примерами агрегатных типов служат кортежи, массивы, списки и др. Нередко встречаются также предопределенные вспомогательные типы, полезные для промышленных разработок, такие так «время», «календарная дата» и пр.

Структурные (агрегатные) типы не следует отождествлять со структурами данных: одни структуры данных непосредственно воплощаются определенными структурными типами, но другие строятся посредством их композиции, чаще всего рекурсивной . Об этом говорит сайт https://intellect.icu . В последнем случае говорят о рекурсивных типах данных[en]. Примером структур данных, которые почти всегда строятся посредством композиции объектов рекурсивного типа, являются бинарные деревья .

По другой классификации типы делятся на самостоятельные и зависимые. Важными разновидностями последних являются ссылочные типы, частным случаем которых, в свою очередь, являются указатели. Ссылки (в том числе и указатели) представляют собой несоставной зависимый тип, значения которого являются адресом в памяти ЭВМ другого значения. Например, в языке Си тип «указатель на целое без знака» записывается как «unsigned *», в языке ML тип «ссылка на целое без знака» записывается как «word ref».

Также типы делятся на мономорфные и полиморфные (см. переменная типа).

Примеры

• примитивные типы, в том числе:
  • логические типы
  • целые типы
  • вещественные типы
• ссылочные типы
• опциональные типы
  • обнуляемые типы
• Композитные типы, в том числе:
  • массивы
  • записи
  • кортежи
  • абстрактные типы ( АТД , англ. Об этом говорит сайт https://intellect.icu . ADT)
• алгебраические типы
  • вариантные типы
• подтипы
• унаследованные типы
• объектные типы, т.е. объекты , значением которых являются типы — например, переменные типов
• частичные типы
• рекурсивные типы
• функциональные типы, например бинарные функции
• универсально квантифицированные типы, такие как параметрические типы
• экзистенциально квантифицированные, такие как модули
• зависимые типы — типы, зависящие от термов (значений)
• уточняющие типы — типы, идентфицирующие подмножества других типов
• Предопределенные типы (являющиеся фактически структурными, но предоставляемые на правах примитивных) для удобства промышленных разработок, такие как «дата», «время», «валюта» и др.

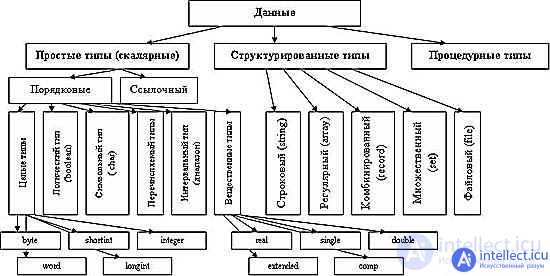
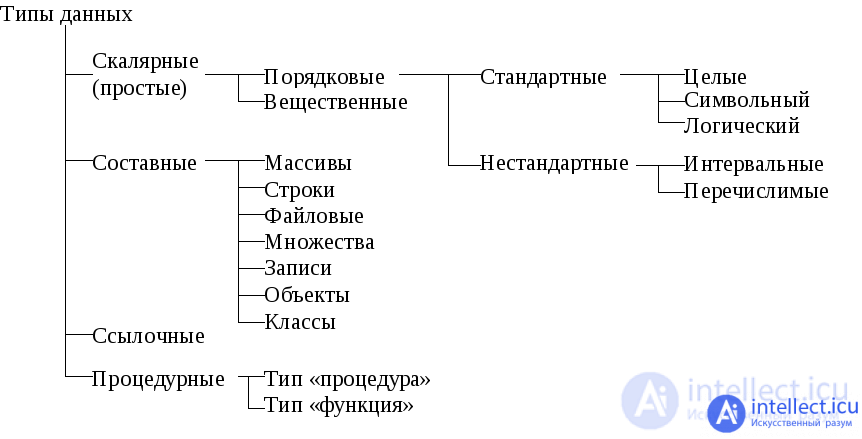
В большинстве языков программирования различают стандартные типы данных и типы, заданные пользователем. К стандартным относят 5 типов:


a) целый (INTEGER);

b) вещественный (REAL) ;

c) логический (BOOLEAN);

d) символьный (CHAR);

e) указательный (POINTER).


К пользовательским относят 2 типа:

a) перечисляемый;

b) диапазонный.


Любой тип данных должен быть охарактеризован областью значений и допустимыми операциями над этим типом данных.

Кроме того в днамически типизированных языках программирования существует понятие - Истинноподобное значение.

Например В JavaScript истинноподобное (truthy) значение — это значение, рассматривающиеся как true в булевом контексте. К истинноподобным значениям относятся все значения кроме ложноподобных значений. То есть все значения истинноподобны кроме false, 0, -0, 0n, "", null, undefined и NaN.

В булевых контекстах JavaScript использует механизм приведения типов.

Типы данных

Примитивные типы

• Логическое , истина или ложь.
• символ
• Числа с плавающей запятой , аппроксимация вещественных чисел с ограниченной точностью .
  • Включая поплавки одинарной и двойной точности IEEE 754 , среди прочего
• Числа с фиксированной точкой
• Целочисленные , целочисленные значения или значения с фиксированной точностью.
• Ссылка (также называемая указателем или дескриптором), небольшое значение, относящееся к адресу другого объекта в памяти, возможно, гораздо большему.
• Перечислимый тип , небольшой набор значений с уникальными именами.
• Дата Время , значение, относящееся к дате и времени

Составные типы или непримитивные типы

• Массив (например, String, представляющий собой массив символов)
• Запись (также называемая ассоциативным массивом, картой или структурой )
• Объединение ( объединение с тегами - это подмножество, также называемое вариантом , вариантной записью, размеченным объединением или непересекающимся объединением)

Абстрактные типы данных

• Контейнер
• Список
• Кортеж
• Multimap
• Задавать
• Мультисет (сумка)
• Стек
• Очередь (пример очереди с приоритетом )
• Двусторонняя очередь
• График (пример Tree , Heap )

Некоторые свойства абстрактных типов данных:

Состав	порядок	Уникальный
Список	да	нет
Ассоциативный массив	нет	да
Задавать	нет	да
Стек	да	нет
Multimap	нет	нет
Мультисет (сумка)	нет	нет
Очередь	да	нет

Порядок означает, что последовательность вставки имеет значение. Уникальный означает, что повторяющиеся элементы не допускаются на основании некоторых встроенных или, альтернативно, определяемых пользователем правил для сравнения элементов.

Virus neutralizer

Game: Perform tasks and rest cool.7 people play!

Play game

1.1 Целый тип - INTEGER

Этот тип включает некоторое подмножество целых, размер которого варьируется от машины к машине. Если для представления целых чисел в машине используется n разрядов, причем используется дополнительный код, то допустимые числа должны удовлетворять условию -2 ^n-1<= x< 2 ^n-1.

Считается, что все операции над данными этого типа выполняются точно и соответствуют обычным правилам арифметики. Если результат выходит за пределы представимого множества, то вычисления будут прерваны. Такое событие называется переполнением.

Числа делятся на знаковые и беззнаковые. Для каждого из них имеется свой диапазон значений:

a)(0..2ⁿ-1) для беззнаковых чисел

b) (-2^N-1.. 2^N-1-1) для знаковых.



При обработке машиной чисел, используется формат со знаком. Если же машинное слово используется для записи и обработки команд и указателей, то в этом случае используется формат без знака.


Операции над целым типом:

a) Сложение.

b) Вычитание.

c) Умножение.

d) Целочисленное деление.

e) Нахождение остатка по модулю.

f) Нахождение экстремума числа (минимума и максимума)

g) Реляционные операции (операции сравнения) (<,>,<=, >=,=,<>)


Примеры:

A div B = C

A mod B = D

C * B + D = A

7 div 3 = 2

7 mod 3 = 1


Во всех операциях, кроме реляционных, в результате получается целое число.

1.2 Вещественный тип - REAL

Вещественные типы образуют ряд подмножеств вещественных чисел, которые представлены в машинных форматах с плавающей точкой. Числа

в формате с плавающей точкой характеризуются целочисленными значениями мантиссы и порядка, которые определяют диапазон изменения

и количество верных знаков в представлении чисел вещественного типа.

X = +/- M * q^(+/-P) - полулогарифмическая форма представления числа, показана на рисунке 2.


937,56 = 93756 * 10^-2 = 0,93756 * 10³



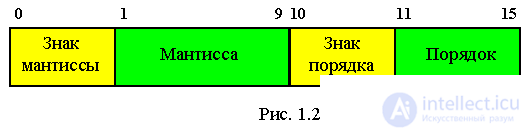
Удвоенная точность необходима для того, чтобы увеличить точность мантиссы.

1.3 Логический тип - BOOLEAN

Стандартный логический тип Boolean (размер-1 байт) представляет собой тип данных, любой элемент которого может принимать лишь 2 значения: True и False.

Над логическими элементами данных выполняются логические операции. Основные из них:

a) Отрицание (NOT)

b) Конъюнкция (AND)

c) Дизъюнкция (OR)

Таблица истинности основных логических функций.





Логические значения получаются также при реляционных операциях с целыми числами.

1.4 Символьный тип - CHAR

Тип CHAR содержит 26 прописных латинских букв и 26 строчных, 10 арабских цифр и некоторое число других графических символов, например, знаки пунктуации.

Подмножества букв и цифр упорядочены и "соприкасаются", т.е.

("A"<= x)&(x <= "Z") - x представляет собой прописную букву

("0"<= x)&(x <= "9") - x представляет собой цифру

Тип CHAR содержит некоторый непечатаемый символ, пробел, его можно

использовать как разделитель.

Операции:

a) Присваивания

b) Сравнения

c) Определения номера данной литеры в системе кодирования. ORD(W_i)

d) Нахождение литеры по номеру. CHR(i)

e) Вызов следующей литеры. SUCC(W_i)

f) Вызов предыдущей литеры. PRED(W_i)

Virus neutralizer

Game: Perform tasks and rest cool.7 people play!

Play game

1.5 Указательный тип - POINTER

Переменная типа указатель является физическим носителем адреса величины базового типа. Cтандартный тип-указатель Pointer дает указатель, не связанный ни с каким конкретным базовым типом. Этот тип совместим с любым другим типом-указателем.

Операции:

a) Присваивания

b) Операции с беззнаковыми целыми числами.

При помощи этих операций можно вычислить адрес данных. В машинном виде эти типы занимают максимально возможную длину.


Например:

ABCD:1234 - значение указателя в шестнадцатеричной системе счисления - относительный адрес.

Первое число (ABCD) - адрес сегмента

Второе число (1234) - адрес внутри сегмента.


Получение абсолютного адреса из относительного:

Для получения абсолютного адреса необходимо произвести сдвиг адреса сегмента влево, и к полученному числу прибавить адрес внутреннего сегмента.


Например:

1. Сдвигаем ABCD на один разряд влево. Получаем АВСD0.
2. Прибавляем 1234. Полученный результат и является абсолютным адресом.

ABCD0

12 3 4

----------

ACF04 - абсолютный адрес данного числа.

1.6 Стандартные типы пользователя

1.6.1 Перечисляемый

Перечисляемый тип определяется конечным набором значений, представленных списком идентификаторов в объявлении типа. Значениям из этого набора присваиваются номера в соответствии с той последовательностью, в которой перечислены идентификаторы. Формат

объявления перечисляемого типа таков:


TYPE<имя> = (<список>);

<список>:= <идентификатор>,[<список>]


Если идентификатор указан в списке значений перечисляемого типа, он считается именем константы, определенной в том блоке, где объявлен перечисляемый тип. Порядковые номера значений в объявлении перечисляемого типа определяются их позициями в списке идентификаторов, причем у первой константы в списке порядковый номер равен нулю. К данным перечисляемого типа относится, например, набор цветов:


TYPE <Цвет> = (Красный, Зеленый, Синий)


Операции те же, что и для символьного типа.

Virus neutralizer

Game: Perform tasks and rest cool.7 people play!

Play game

1.6.2 Диапазонный или интервальный

В любом порядковом типе можно выделить подмножество значений, определяемое минимальным и максимальным значениями, в которое входят все значения исходного типа, находящиеся в этих границах, включая сами границы. Такое подмножество определяет диапазонный тип. Он задается указанием минимального и максимального значений, разделенных двумя точками.


TYPE T=[ MIN..MAX ]

TYPE <Час>=[1..60]


Минимальное значение при определении такого типа не должно быть больше максимального.

Самоприменение типов данных

Тип может быть параметризован другим типом, в соответствии с принципами абстракции и параметричности. Например, для реализации функции сортировки последовательностей нет необходимости знать все свойства составляющих ее элементов — необходимо лишь, чтобы они допускали операцию сравнения — и тогда составной тип «последовательность» может быть определен как параметрически полиморфный. Это означает, что его компоненты определяются с использованием не конкретных типов (таких как «целое» или «массив целых»), а параметров-типов. Такие параметры называются переменными типа (англ. type variable) — они используются в определении полиморфного типа так же, как параметры-значения в определении функции. Подстановка конкретных типов в качестве фактических параметров для полиморфного типа порождает мономорфный тип. Таким образом, параметрически полиморфный тип представляет собой конструктор типов, то есть оператор над типами в арифметике типов.

Определение функции сортировки как параметрически полиморфной означает, что она сортирует абстрактную последовательность, то есть последовательность из элементов некоторого (неизвестного) типа. Для функции в этом случае требуется знать о своем параметре лишь два свойства — то, что он представляет собойпоследовательность, и что для ее элементов определена операция сравнения. Рассмотрение параметров процедурным, а не декларативным, образом (т.е. их использование на основе поведения, а не значения) позволяет использовать одну функцию сортировки для любых последовательностей — для последовательностей целых чисел, для последовательностей строк, для последовательностей последовательностей булевых значений, и т. д. — и существенно повышает коэффициентповторного использования кода. Ту же гибкость обеспечивает и динамическая типизация, однако, в отличие от параметрического полиморфизма, первая приводит к накладным расходам. Параметрический полиморфизм наиболее развит в языках, типизированных по Хиндли — Милнеру, то есть потомках языка ML. В объектно-ориентированном программировании параметрический полиморфизм принято называть обобщенным программированием.

Несмотря на очевидные преимущества параметрического полиморфизма, порой возникает необходимость обеспечивать различное поведение для разных подтипов одного общего типа, либо аналогичное поведение для несовместимых типов — т.е. в тех или иных формах ad hoc полиморфизма. Однако, ему не существует математического обоснования, так что требование типобезопасности[en] долгое время затрудняло его использование. Ad hoc полиморфизм реализовывался внутри параметрически полиморфной системы типов посредством различных трюков. Для этой цели использовались либо вариантные типы[en], либо параметрические модули (функторы), либо так называемые «значения, индексированные типами» (англ. type-indexed values), которые, в свою очередь, также имеют ряд реализаций . Классы типов, появившиеся в языке Haskell, предоставили более изящное решение этой проблемы.

Если рассматриваемой информационной сущностью является тип, то назначение ей типа приведет к понятию «тип типа», или «метатип». В теории типов это понятие носит название «род типов» (англ. kind of a type или type kind). Например, род «*» включает все типы, а род «* -> *» включает все унарные конструкторы типов. Рода явным образом применяются при полнотиповом программировании — например, в виде конструкторов типов в языках семейства ML.

Расширение безопасной полиморфной системы типов классами[en] и родами типов сделало Haskell первым типизированным в полной мере языком. Полученная система типов оказала влияние на другие языки (например, Scala, Agda).

Ограниченная форма метатипов присутствует также в ряде объектно-ориентированных языков в форме метаклассов. В потомках языка Smalltalk (например, Python) всякая сущность в программе является объектом, имеющим тип, который сам также является объектом — таким образом, метатипы являются естественной частью языка. В языке C++ отдельно от основной системы типов языка реализована подсистема RTTI, также предоставляющая информацию о типе в виде специальной структуры.

Динамическое выяснение метатипов называется отражением (а также рефлексивностью или интроспекцией).

В математике, логике и компьютерных науках теорией типов считается какая-либо формальная система, являющаяся альтернативой наивной теории множеств, сопровождаемая классификацией элементов такой системы с помощью типов, образующих некоторую иерархию. Также под теорией типов понимают изучение подобных формализмов.

Теория типов — математически формализованная база для проектирования, анализа и изучения систем типов данных в теории языков программирования (раздел информатики). Многие программисты используют это понятие для обозначения любого аналитического труда, изучающего системы типов в языках программирования. В научных кругах под теорией типов чаще всего понимают более узкий раздел дискретной математики, в частности λ-исчисление с типами.

Современная теория типов была частично разработана в процессе разрешения парадокса Рассела и во многом базируется на работе Бертрана Рассела и Альфреда Уайтхеда «Principia mathematica»

Представление в компьютере

Наиболее заметным отличием реального программирования от формальной теории информации является рассмотрение вопросов эффективности не только в терминахО-нотации, но и с позиций экономической целесообразности воплощения тех или иных требований в физически изготовляемой ЭВМ. И в первую очередь это сказывается на допустимой точности вычислений: понятие «число» на ЭВМ на практике не тождественно понятию числа в арифметике. Число на ЭВМ представляется ячейкойпамяти, размер которой определяется архитектурой ЭВМ, и диапазон значений числа ограничивается размером этой ячейки. Например, процессоры архитектуры Intel x86 предоставляют ячейки, размер которых в байтах задается степенью двойки: 1, 2, 4, 8, 16 и т. д. Процессоры архитектуры Сетунь предоставляли ячейки, размер которых в трайтах задавался кратным тройке: 1, 3, 6, 9 и т. д.

Попытка записи в ячейку значения, превышающего максимально допустимый для нее предел (который известен) приводит к ошибке переполнения. При необходимости расчетов на более крупных числах используется специальная методика, называемая длинной арифметикой, которая в силу значительной ресурсоемкости не может осуществляться в реальном времени. Для наиболее распространенных в настоящее время архитектур ЭВМ «родным» является размер ячеек в 32 и 64 бит (то есть 4 и 8байт).

Кроме того, целые и вещественные числа имеют разное представление в этих ячейках: неотрицательные целые представляются непосредственно, отрицательные целые — в дополнительном коде, а вещественные кодируются особым образом. Из-за этих различий сложение чисел «1» и «0.1», которое в теории дает значение «1.1», на ЭВМ непосредственно невозможно. Для его осуществления необходимо сперва выполнить преобразование типа, породив на основании значения целого типа «1» новое значение вещественного типа «1.0», и лишь затем сложить «1.0» и «0.1». В силу специфики реализации вещественных чисел на ЭВМ, такое преобразование осуществляется не абсолютно точно, а с некоторой долей приближения. По той же причине сильно типизированные языки (например, Standard ML) рассматривают вещественный тип как «не допускающий проверку на равенство[en]».

Важное значение также имеет понятие о выравнивании данных.

Контрольные вопросы:

1. Каковы основные характеристики структур данных?
2. Какие типы данных вы знаете ?
3. Какие из них относятся к стандартным, а какие к пользовательским ?
4. Как представляются вещественные числа ?
5. Что представляют собой данные логического типа ?
6. Какие типы данных относятся к стандартным пользовательским ?
7. Какому условию должны удовлетворять допустимые числа типа INTEGER ?
8. Какие операции можно производить над целыми числами ?
9. Перечислите булевские операции.
10. Какова структура типа CHAR ?
11. Какие операции возможны над данными этого типа ?
12. Что можно вычислить с помощью данных указательного типа ?
13. Что представляет собой перечисляемый тип данных?
14. Как задается диапазонный тип ?

Вау!! 😲 Ты еще не читал? Это зря!

• Система типов
• Алгебраический тип данных, конструктор данных, конструктор типов
• Рекурсивный тип данных
• Подтип
• Функциональный тип
• Полиморфизм типов и переменная типа
• Класс типов

• Теория типов

• Род ( теория типов )

• Абстрактный тип данных

• Истинноподобное значение

• структуры днных структуры данных ,
• теория типов , базовые вычислительные формализмы ,
• типы данных в javascript , типы переменных в javascript ,
• непрозрачный тип данных , odt ,
• типы данных в php ,
• тип данных - класс ,
• переменная

На этом все! Теперь вы знаете все про типы данных, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое типы данных и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.