Лекция
Привет, Вы узнаете о том , что такое связные списки на c , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое связные списки на c , pascal + тесты+ ы сортировки поиска вставки в списки , настоятельно рекомендую прочитать все из категории Структуры данных.
Понятие "списки" включает в себя самые разные структуры данных. Это могут быть и массивы, в том числе массивы записей, и специальные динамические структуры данных, и даже деревья. Общим для них является то, что они содержат набор записей одного вида, ограниченный по размеру или неограниченный, упорядоченный или неупорядоченный. Данные, хранящиеся в этих записях, обычно логически связаны между собой, например, фамилии студентов одной группы и т.п. В тексте программы такая связь может выражаться в том, что все такие элементы хранятся в одном и том же массиве как непрерывном блоке памяти. Но кроме общего имени массива (и адреса его начала) между этими элементами никакой другой физической связи нет, и на физическом уровне подобные списки могут быть названы "несвЯзными" (или, что (почти) то же самое, "несвязанными"). Т.е. внутри них нет связей (их элементы не связаны друг с другом физически).
Типичным примером незвязного (физически) списка является массив. В этой главе мы рассмотрим те самые "специальные динамические структуры данных", которые и получили название свЯзных списков.
Вспомним общие черты очередей и стеков:
Связные списки свободны от этих ограничений. Они допускают гибкие методы доступа; извлечение (чтение) элемента из списка не приводит к удалению его из списка и потере данных. Для фактического удаления элемента из связного списка требуется специальная процедура.
Связные списки представляют собой (как ужЕ было сказано) динамические (фактически, линейные!) структуры данных (динамические цепочки звеньев), в которых однотипные элементы (звенья) каким-либо образом связаны между собой, обычно на физическом уровне. Связь между элементами можно осуществить за счет хранения в одном элементе адреса другого такого же элемента (того же типа). Т.е. каждый информационный элемент содержит внутри себя указатель на собственный тип. Учитывая, что кроме этого указателя должны присутствовать полезные данные, тип информационного элемента оказываетсязаписью. Например, для простейшего вида списка этот тип может быть следующим (на языках Си/Си++):
struct Link1
{
int data;
Link1* next;
};
Классификация связных списков. По числу связей (и одновременно, направлению) списки бывают односвязными (однонаправленными), двусвязными (двунаправленными) и многосвязными.
По способу организации связей (или по архитектуре) списки могут быть линейными и кольцевыми (циклическими). (Если список не является ни линейным, ни кольцевым, то остается единственный вариант – ветвящийся список, фактически являющийся одной из древовидных структур данных.)
По степени упорядоченности хранимых данных списки могут быть упорядоченными и неупорядоченными. Такое разделение иногда бывает удобно на практике, но для поддержания упорядоченности списков приходится прибегать к специальным мерам.
Для списков, по сравнению с очередями и стеками, имеется значительно больше операций, которые включают в себя:
Рассмотрим основные из этих операций для каждого вида списка отдельно, вместе с особенностями этих видов списков.
Линейный односвязный список является самым простым видом связных списков. Такой список можно определить с помощью описаний типов (см. пример 1).
Процедуры работы с линейным односвязным списком на языке Паскальrel1 = ^elem; (* Указатель на запись *) elem = record next: rel1; data: <Тип хранимых данных> (* Любой допустимый тип данных *) end; var L1: rel1;  Ддя того, чтобы такие операции, как добавление или удаление звена, выполнялись одинаково, независимо от места их выполнения в списке, удобно использоватьведущее или заглавное звено - самое первое звено списка, в котором не обязаны храниться полезные данные. Его создание для односвязного списка можно осуществить следующим образом: var a, L1: list1; begin ... new(L1); L1^.next := nil; a := L1; ... Указатель на начало списка L1, значением которого является адрес ведущего звена, представляет список как единый программный объект. Указатель на следующий элемент в последнем звене списка имеет значение nil(NULL или просто 0 в Си/Си++), что является признаком линейного списка. procedure insert1(link: rel1; info: <Тип>); var q: rel1; begin new(q); q^.data := info; q^.next := link^.next; link^.next := q end; procedure delete1(link:rel1); var q: rel1; begin if link^.next <> nil then begin q := link^.next; link^.next := link^.next^.next; dispose(q); end end; function search1(l: rel1; info: <Тип>; var r: rel1):boolean; var q: rel1; begin search1 := false; r := nil; q := l^.next; while (q <> nil) and (r <> nil) do begin if q^.data = info then begin search := true; r := q end; q := q^.next end end; |
Процедуры добавления и удаления звеньев являются критическими с точки зрения сохранения целостности списка. При неправильном выполнении этих процедур (т.е. при неправильной очередности выполнения операций присваивания) возможны 2 ошибочные ситуации:
1. Список "рвется" по месту вставки или удаления звена, и звено, оказавшее последним, замыкается либо само на себя (чаще всего) (т.е. указатель next или аналогичный ему в этом звене получает значение адреса этого же звена), либо на одно из предшествующих звеньев (в зависимости от неправильной реализации операций вставки или удаления звена). При попытке просмотра списка процедура просмотра зацикливается и бесконечно выводит содержимое одного и того же звена (или нескольких звеньев).
2. Список так же "рвется" по месту вставки или удаления звена, но указатель в звене, ставшем последним, получает какое-то произвольное значение, которое трактуется как адрес следующего звена (реально не существующего), у которого также есть указатель next, содержащий какой-то адрес, и так далее, до тех пор, пока случайно не попадется блок данных, для которого указатель next не будер равен нулю. При попытке просмотра списка на дисплей сначала выводятся правильные данные, а затем случайный набор символов.
В обоих случаях к звеньям в "оторвавшейся" части ("хвосте") списка больше нет доступа, и хранящиеся в них данные можно считать потерянными.
Для предовращения возникновения таких ошибок следует соблюдать правильный порядок проведения связей (т.е. присваивания указателей) при вставке нового звена и удалении существующего (очередность операций указана):
|
Возможность перемещаться по 1-связному списку только в одном направлении приводит к тому, что при удалении звена приходится задавать не реально удаляемое звено, а предшествующее ему. Это делается для того, чтобы можно было скорректировать связь для предшествующего звена, добраться до которого от удаляемого иначе невозможно.
|
Одной из наиболее простых операций со всеми типами списков является их прохождение, т.е. поочередное получение доступа ко всем элементам. Приведем процедуру, реализующую эту операцию дляпросмотра списка (другие варианты использования прохождения – поиск данных и сохранение списка в файл). В случае перемещения по 2-связному списку в "прямом" направлении эта процедура являетсяодинаковой для 1- и 2-связного линейных списков.
|
void Show(Link1* link) { Link1 *q = link->next; // Учитывается наличие "пустого" ведущего звена while (q) // или while(q!=NULL) { cout<<q->data<<' '; // или другая операция q = q->next; // Переход по списку } cout<<endl; } |
Поиск в списке является вариантом операции просмотра и отличается тем, что:
1. вместо операции вывода на экран (cout<<q->data) используется операция сравнения искомых данных с хранящимися в звеньях списка;
2. если искомые данные найдены, нет необходимости перемещаться по списку дальше.
Поиск в односвязных списках имеет следующую особенность. Если он выполняется в сочетании с удалением, то результатом поиска может (или должно) быть не то звено, в котором содержатся искомые данные, а предшествующее ему. В итоге для поиска в списке могут потребоваться либо две различные процедуры – "обычная" и находящая предыдущее звено, либо одна универсальная, позволяющая найти оба звена – с искомыми данными и предшествующее ему. Рассмотрим в качестве примера именно этот вариант
|
int Search(Link1* Start, // Точка начала поиска Link1*& Find, // Указатель для звена с искомыми данными Link1*& Pred, // Указатель для предыдущего звена int Key) // Ключ поиска { Link1* Cur = Start->next; // Текущее звено Pred = Start; // Предыдущее звено ("отстает" на 1 шаг от текущего) int Success = 0; // Признак успеха поиска (установлен в 0) while (Cur && !Success) // Операция логическое "И" { if (Cur->data == Key) // нашли { Find = Cur; // Запоминание найденного звена Success = 1; // Установка в 1 признака успеха break; // Выход из цикла при удачном поиске } Pred = Cur; // Перемещение предыдущего звена Cur = Cur->next; // Переход по списку вперед } return Success; } Следует отметить, что возможны разные (в том числе более короткие) варианты реализации такого алгоритма, например, без переменной Success (вместо нее используется указатель Find, который до начала поиска должен получить значениеNULL и сохранить его при неудачном поиске). Процедура, которая находит только искомое звено, является более простой, – в ней не нужен указатель Pred и все операторы, в которых он используется. Похожая процедура применяется для 1-связного кольцевого списка. Отличие ее от рассмотренного примера заключается в условии продолжения цикла в оператореwhile: while(Cur != Start && !Success) // Для кольцевого списка |
Ведущее (или заглавное) звено. Все приведенные выше примеры на языке Си++ подразумевают наличие в списке ведущего звена. Создаваться это звено может либо отдельной процедурой, либо следующим набором операторов (эти же операторы и будут находиться в процедуре):
Link1 *L1 = new Link1; // Выделение памяти под звено
L1->next = NULL; // Ведущее звено одновременно является последним
Возможна работа со связным списком и без выделенного ведущего звена, т.е. первое звено является обычным, в нем содержатся полезные данные. Именно такой вид списка использовался для организациистека. Еще один пример использования подобных списков - очередь.
|
void queue_in(Link2*& q, // "Голова" очереди Link2*& e, // "Хвост" очереди int k) // Вводимые данные { Link2* n = new node; // Новый узел n->data = k; n->next = q; if (q) q->prev = n; else e = n; n->prev = 0; q = n; } int queue_out(Link2*& q, Link2*& e) { int k = e->data; Link2* d = e; e = d->prev; if (e) e->next = 0; else q = e; delete d; return k; } Для упрощения обработки "головы" и "хвоста" очереди использован 2-связный список. |
В остальных случаях (т.е. для обычных списков) использование ведущего звена является предпочтительным, т.к. позволяет избежать проверок при добавлении и удалении звеньев.
Недостатки односвязного списка заключаются в следующем:
1. По такому списку можно перемещаться только от начального звена к конечному. Начинать можно с любого звена в списке, но если вдруг возникнет необходимость обратиться к предшествующим элементам, придется начинать с начального звена, что неудобно, нерационально и усложняет алгоритмы обработки данных.
2. Наличие только одной связи снижает надежность хранения данных в 1-связном списке.
3. Следствием первого недостатка является усложнение взаимодействия операций поиска и удаления.
Достоинствами этого списка являются меньший расход памяти по сравнению с другими свЯзными динамическими структурами данных (всего 1 указатель) и простота операций.
Этот список свободен от недостатков, присущих односвязному списку. Для этого в каждое звено добавлен еще один указатель на тип звена, значением которого является адрес предыдущего звена списка. Тип звена на языках Си/Си++:
struct Link2
{
int data;
Link2 *next, *prev;
};
Структура списка будет выглядеть следующим образом (значения нулевых указателей показаны для языка Паскаль):

Ведущее звено этого списка создается следующим набором операторов:
Link2 *L2 = new Link2;
L2->next = NULL;
L2->prev = NULL;
По операторам создания ведущего звена можно судить о том, является список, 1- или 2-связным, линейным или кольцевым. Нулевые значения указателей next и prev являются признаком линейного списка.
Графически состояние списка после создания ведущего звена может быть отображено следующим образом:
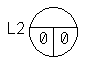
Преимущества двусвязного списка:
Операции с 2-связным списком.Все, что касалось операций добавления звена и его удаления для 1-связного списка, справедливо и для 2-связного. Так же должен соблюдаться правильный порядок проведения (или удаления) связей между звеньями, но таких операций стало больше, т.к. должны обрабатываться 2 указателя. Кроме того, каждая из операций обладает дополнительыми особенностями:
1. При добавлении нового звена в пустой список, т.е. содержащий только ведущее звено (см. предыдущий рисунок), или при добавлении звена в конец списка (для пустого списка обе эти ситуации совпадают) необходимо проверять наличие звена, которое будет следующим за добавляемым (для пустого списка или конца списка такого звена нет, а значит нет и указателя, обозначающего связь). Такая же проверка должна выполняться при удалении звена.
2. Возможность перемещаться по списку в обоих направлениях позволяет напрямую задавать удаляемое звено (а не ему предшествующее, как в 1-связном списке). Следствием этого является упрощение как операции удаления, так и операции поиска.
|
void Insert2(Link2* St, int data) { Link2* q = new Link2; // 1 Выделение памяти под звено q->data = data; // 2 Ввод данных q->next = St->next; // 3 Проведение связи от нового звена вперед q->prev = St; // 4 Проведение связи от нового звена назад St->next = q; // 5 Проведение связи от предыдущего звена к новому if (q->next) // Проверка наличия следующего звена q->next->prev = q; // 6 Проведение связи от следующего звена к новому }
void Delete2(Link2* del) { del->prev->next = del->next; // 1 Обработка связи вперед if (del->next) del->next->prev = del->prev; // 2 Обработка связи назад delete del; // 3 Освобождение памяти }
int Search2(Link2* Start, Link2*& Find, int Key) { Link2* Cur=Start->next; int Success = 0; while (Cur && !Success) { if (Cur->data == Key) { Find = Cur; Success = 1; break; } Cur = Cur->next; } return Success; } Эта процедура поиска фактически является (за исключением типа данных Link2вместо Link1) процедурой "обычного" поиска (т.е. Об этом говорит сайт https://intellect.icu . не для удаления) в 1-связном списке. |
Операция просмотра списка в прямом направлении ничем не отличается от просмотра 1-связного списка.
Если значение указателя последнего звена линейного односвязного списка заменить с nil (или NULL) на адрес ведущего звена, то линейный список превратится в односвязный кольцевой список.
Для двусвязного списка, кроме того, нужно заменить с nil на адрес последнего звена значение второго указателя в ведущем звене. Получится двусвязный кольцевой (циклический) список.
В односвязном кольцевом списке можно переходить от последнего звена к заглавному, а в двусвязном – еще и от заглавного к последнему.
Двусвязный кольцевой список выглядит так:
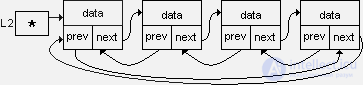
Кольцевой список, как и линейный, идентифицируется как единый программный объект указателем, например L2, значением которого является адрес заглавного звена.
Возможен другой вариант организации кольцевого списка:

Оба варианта сопоставимы по сложности. Для первого варианта проще выполняется вставка нового элемента как в начало списка (после заглавного звена), так и в конец – так как вставка звена в конец кольцевого списка эквивалентна вставке перед заглавным звеном, но каждый раз при циклической обработке списка нужно проверять, не является ли текущее звено заглавным (или не совпадает ли текущее звено с точкой начала обработки).
Рассмотрим операции с кольцевыми списками.
Отсутствие "последнего" звена приводит к еще большему упрощению операций добавления и удаления, по сравнению с 1- и 2-связным линейным списком. Например, для 1-связного кольцевого списка в процедуре удаления отсутствует оператор if – проверка на существование звена, следующего за заданным (в кольцевом списке такое звено всегда есть). Такие же операторы отсутствуют в процедурах добавления и удаления звеньев для 2-связного кольцевого списка.
При циклической обработке кольцевого списка нужно учесть, что формально последнего звена нет.
Программа работы с двусвязным кольцевым списком на языке Паскальrel2 = ^elem2; elem2 = record next: rel1; prev: rel2; data: <Тип хранимых данных> end; list2 = rel2; procedure insert2(pred: rel2; info: <Тип>); var q: rel2; begin new(q); (* Создание нового звена *) q^.data := info; q^.next := pred^.next; q^.prev := pred^.next^.prev; pred^.next.prev := q; pred^.next := q end; При вставке в начало списка (после заглавного звена) нужно указать в качестве аргумента pred адрес заглавного звена, то есть указатель на список L2. procedure delete2(del: rel2); begin del^.next^.prev := del^.prev; del^.prev^.next := del^.next; dispose(del); end; function search2(list: rel2; info: <Тип>; var point: rel2):boolean; var p,q: rel2; b:boolean; begin b := false; point := nil; p := list; q := p^.next; while (p <> q) and (not b) do begin if q^.data = info then begin b := true; point := q end; q := q^.next end; search2 := b end; ... ... var l2: list2; r: rel2; begin (* Создание заглавного звена *) new(r); r^.next := r; r^.pred := r; l2 := r; ... ... end. Процедуры работы с двусвязным кольцевым списком на языке Си++Тип данных для кольцевого 2-связного списка такой же, как и для 2-связного линейного. То же самое справедливо для 1-связных списков. По типу звена списканельзя судить о его архитектуре, можно - только о числе связей. Добавление звена в произвольную позицию за ведущим звеном{ Link2* Loc = new Link2; // 1 Loc->Value = data; // 2 Loc->next = Pred->next; // 3 Loc->prev = Pred; // 4 Pred->next = Loc; // 5 Loc->next->prev = Loc; // 6 } Удаление звена из любого места списка за ведущим звеном{ Del->prev->next = Del->next; // 1 Del->next->prev = Del->prev; // 2 delete Del; // 3 } Поиск{ Link2* Cur = Start->next; int Success = 0; while (Cur != Start && !Success) { if (Cur->Value == Key) { Find = Cur; Success = 1; break; } Cur = Cur->next; } return Success; } Прекращение поиска в случае неудачи происходит при достижении "текущим" указателем Cur точки начала поиска Start, т.е. при невыполнении условия в оператореwhile: while(Cur != Start ... ) |
Ведущее звено кольцевого 2-связного списка создается набором операторов:
Link2 *L2 = new Link2;
L2->next = L2;
L2->prev = L2;
Графически состояние списка после создания этого звена может быть представлено таким образом:

Многосвязные списки представляют собой динамические структуры данных, в основу которых положены 1- или 2-связные списки, в которых имеются дополнительные связи между звеньями. Чаще всего, такие связи проводятся между далеко отстоящими звеньями, например, обозначающими категории данных. Пример многосвязного списка показан на следующем рисунке.

Переход между звеньями АА и БА может выполнен по дополнительной связи, в обход звеньев АБ и АВ. Из-за такого характера перемещения эти списки иногда называют скип-списками (skip – перепрыгивать). А при характере размещения данных, подобном показанному на этом рисунке, такие списки называют словарными (иногда просто словарями, но термин "словарь" может использоваться в теории структур данных в разных значениях).
односвязный линейный список
================
struct Link1
{
int Value;
Link1* next;
};
линейный:
=========
Link1 *L1=new Link1;
L1->next=NULL;
Добавление звена в произвольную позицию за ведущим звеном:
void Insert(Link1* Pred,int data)
{
Link1* Loc=new Link1;
Loc->Value=data;
Loc->next=Pred->next;
Pred->next=Loc;
}
Удаление звена из любого места списка за ведущим звеном:
void Delete(Link1* Pred)
{
Link1* Loc;
if(Pred->next)
{
Loc=Pred->next;
Pred->next=Loc->next;
delete Loc;
}
}
Универсальная процедура поиска (находит звено с ключом поиска
и предшествующее ему):
int Search(Link1* Start,Link1*& Find,Link1*& Pred,int Key)
{
Link1* Cur=Start; // ->next;
Pred=Start;
int Success=0;
while(Cur && !Success)
{
if(Cur->Value==Key)
{
Find=Cur;
Success=1;
break;
}
Pred=Cur;
Cur=Cur->next;
}
return Success;
}
Реверсирование (обращение) списка
=================================
- с циклом "while"
void ReverseW(Link1* L)
{
Link1* a=L->next,*b=a,*c=NULL;
while(b)
{
a=b;
b=a->next;
a->next=c;
c=a;
}
L->next=a;
}
Link1* ReverseW1(Link1* L)
{
Link1* a=L->next,*b,*c=NULL;
while(a)
{
b=a->next;
a->next=c;
c=a;
a=b;
}
return c;
}
- с циклом "for"
void Reverse(Link1* L)
{
Link1* a=L->next,*b=a,*c=NULL;
for(;b;a=b,b=a->next,a->next=c,c=a);
L->next=a;
}
Link1* Reverse1(Link1* L)
{
Link1* a=L->next,*b,*c=NULL;
for(;a;b=a->next,a->next=c,c=a,a=b);
return c;
}
Сортировки
==========
Пузырьковая:
------------
- с процедурами удаления и дополнения
void BubbleListSort(Link1* Start)
{
int buf,n=0;
Link1* Last,*b,*b0;
for(Last=NULL;Last!=Start->next;)
{
for(b0=Start,b=Start->next;b->next!=Last;b0=b0->next)
{
if(b->Value>b->next->Value)
{
buf=b->next->Value;
Delete(b);
Insert(b0,buf);
}
else
b=b->next;
}
Last=b;
}
}
- с заменой значений указателей
void Bubble2ListSort(Link1* Start)
{
int n=0;
Link1* Last,*b,*b0;
for(Last=NULL;Last!=Start->next;)
{
for(b0=Start,b=Start->next;b->next!=Last;b0=b0->next)
{
if(b->Value>b->next->Value)
{
b0->next=b->next; // Перестановка звеньев
b->next=b->next->next;
b0->next->next=b;
}
else
b=b->next;
}
Last=b;
}
}
- с премещением данных между звеньями
void BubbleListSortSimple(Link1* Start)
{
Link1* q;
int buf,n=0;
for(Link1* Last=NULL,*e=Start->next;e->next;e=e->next)
{
for(q=Start->next;q->next!=Last;q=q->next)
{
if(q->Value>q->next->Value)
{
buf=q->Value;
q->Value=q->next->Value;
q->next->Value=buf;
}
}
Last=q;
}
}
Сортировка отбором:
-------------------
- аналог сортировки массива с процедурами дополнения и удаления
void SelectSort(Link1* Start)
{
int min,change,n=0;
Link1* Beg,*predmin,*b;
for(Beg=Start;Beg->next;Beg=Beg->next)
{
change=0;
min=Beg->next->Value;
for(b=Beg;b->next;b=b->next)
{
if(b->next->Value<min)
{
min=b->next->Value;
predmin=b;
change=1;
}
}
if(change)
{
Delete(predmin);
Insert(Beg,min);
}
}
}
- с заменой значений указателей
void Select1(Link1* Start)
{
int min,change,n=0;
Link1* Beg,*predmin,*b,*Lmin;
for(Beg=Start;Beg->next;Beg=Beg->next)
{
change=0;
min=Beg->next->Value;
for(b=Beg;b->next;b=b->next)
{
if(b->next->Value<min)
{
min=b->next->Value;
predmin=b;
change=1;
}
}
if(change)
{
Lmin=predmin->next;
predmin->next=Lmin->next;
Lmin->next=Beg->next;
Beg->next=Lmin;
}
}
}
Сортировка вставками:
---------------------
- аналог сортировки массива
void InsertSort(Link1* Start)
{
int buf,n=0;
Link1* Beg,*a,*b,*Beg1=new Link1;
Beg1->next=NULL;
for(Beg=Start->next;Beg;Beg=a)
{
a=Beg->next;
for(b=Beg1;b->next;b=b->next)
if(b->next->Value>Beg->Value)
break;
Beg->next=b->next;
b->next=Beg;
}
Start->next=Beg1->next;
delete Beg1;
}
- аналог предыдущей с циклом "while"
void InsertWSort(Link1* Start)
{
int buf,n=0;
Link1* Beg,*a,*b,*Beg1=new Link1;
Beg1->next=NULL;
Beg=Start->next; // for(Beg=Start->next;Beg;Beg=a)
while(Beg)
{
a=Beg->next;
b=Beg1; // for(b=Beg1;b->next;b=b->next)
while(b->next)
{
if(b->next->Value>Beg->Value)
break;
b=b->next;
}
Beg->next=b->next;
b->next=Beg;
Beg=a;
}
Start->next=Beg1->next;
delete Beg1;
}
Сортировка Шелла (предварительно):
------------------------------------------
void ShellSort(Link1* Start)
{
const int N=5;
int steps[N]={9,5,3,2,1};
int buf,n=0;
Link1* Beg,*a,*b,*Beg1;//=new Link1;
for(int i=0;i<N;i++)
{
Beg1=new Link1;
Beg1->next=NULL;
for(Beg=Start->next;Beg;Beg=a)
{
a=Beg->next;
for(b=Beg1;b->next;b=b->next)
if(b->next->Value>Beg->Value)
break;
Beg->next=b->next;
b->next=Beg;
}
Start->next=Beg1->next;
delete Beg1;
}
}
двусвязный линейный список
================
struct Link2
{
int Value;
Link2* next,*prev;
};
линейный:
=========
Link2 *L1=new Link2;
L1->next=NULL;
L1->prev=NULL;
Добавление звена в произвольную позицию за ведущим звеном:
void Insert(Link2* Pred,int data)
{
Link2* Loc=new Link2;
Loc->Value=data;
Loc->next=Pred->next;
Loc->prev=Pred;
Pred->next=Loc;
if(Loc->next)
Loc->next->prev=Loc;
}
Удаление звена из любого места списка за ведущим звеном:
void Delete(Link2* Del)
{
Del->prev->next=Del->next;
if(Del->next)
Del->next->prev=Del->prev;
delete Del;
}
Вывод содержимого списка в обратном порядке:
void ShowReverse(Link2* Start)
{
Link2* Loc=Start->next;
while(Loc->next)
Loc=Loc->next;
while(Loc!=Start)
{
cout<<Loc->Value<<' ';
Loc=Loc->prev;
}
cout<<endl;
}
Поиск:
int Search(Link2* Start,Link2*& Find,int Key)
{
Link2* Cur=Start->next;
int Success=0;
while(Cur && !Success)
{
if(Cur->Value==Key)
{
Find=Cur;
Success=1;
break;
}
Cur=Cur->next;
}
return Success;
}
Реверсирование (обращение) списка
=================================
- с циклом "while"
void ReverseW(Link2* L)
{
Link2* a=L->next,*b=a,*c=NULL;
while(b)
{
a=b;
b=a->next;
if(b)
a->prev=b;
else
a->prev=L;
a->next=c;
c=a;
}
L->next=a;
}
Link2* ReverseW1(Link2* L)
{
Link2* a=L->next,*b,*c=NULL;
while(a)
{
b=a->next;
if(b)
a->prev=b;
else
a->prev=L;
a->next=c;
c=a;
a=b;
}
return c;
}
- с циклом "for"
void Reverse(Link2* L)
{
Link2* a=L->next;
for(Link2 *b=a,*c=NULL;b;a=b,b=a->next,b?a->prev=b:a->prev=L,a->next=c,c=a);
L->next=a;
}
Link2* Reverse1(Link2* L)
{
Link2* a=L->next,*c=NULL;
for(Link2 *b;a;b=a->next,b?a->prev=b:a->prev=L,a->next=c,c=a,a=b);
return c;
}
Сортировки
==========
Пузырьковая:
------------
- с процедурами удаления и дополнения
void BubbleListSort(Link2* Start)
{
int buf,n=0;
Link2* Last,*b,*b0;
for(Last=NULL;Last!=Start->next;)
{
for(b0=Start,b=Start->next;b->next!=Last;b0=b0->next)
{
if(b->Value>b->next->Value)
{
buf=b->next->Value;
Delete(b->next);
Insert(b0,buf);
}
else
b=b->next;
}
Last=b;
}
}
- с заменой значений указателей
void Bubble2ListSort(Link2* Start)
{
int n=0;
Link2* Last,*b,*b0;
for(Last=NULL;Last!=Start->next;)
{
for(b0=Start,b=Start->next;b->next!=Last;b0=b0->next)
{
if(b->Value>b->next->Value)
{
b0->next=b->next; // Перестановка звеньев // I
b->next->prev=b0;
b->next=b->next->next; // II
if(b->next)
b->next->prev=b;
b0->next->next=b; // III
b->prev=b0->next;
}
else
b=b->next;
}
Last=b;
}
}
- с премещением данных между звеньями
void BubbleListSortSimple(Link2* Start)
{
Link2* q;
int buf,n=0;
for(Link2* Last=NULL,*e=Start->next;e->next;e=e->next)
{
for(q=Start->next;q->next!=Last;q=q->next)
{
if(q->Value>q->next->Value)
{
buf=q->Value;
q->Value=q->next->Value;
q->next->Value=buf;
}
}
Last=q;
}
}
Сортировка отбором:
-------------------
- аналог сортировки массива с процедурами дополнения и удаления
void SelectSort(Link2* Start)
{
int min,change,n=0;
Link2* Beg,*Lmin,*b;
for(Beg=Start;Beg->next;Beg=Beg->next)
{
change=0;
min=Beg->next->Value;
for(b=Beg->next;b;b=b->next)
{
if(b->Value<min)
{
min=b->Value;
Lmin=b;
change=1;
}
}
if(change)
{
Delete(Lmin);
Insert(Beg,min);
}
}
}
- с заменой значений указателей
void Select1(Link2* Start)
{
int min,change,n=0;
Link2* Beg,*b,*Lmin;
for(Beg=Start;Beg->next;Beg=Beg->next)
{
change=0;
min=Beg->next->Value;
for(b=Beg->next;b;b=b->next)
{
if(b->Value<min)
{
min=b->Value;
Lmin=b;
change=1;
}
}
if(change)
{
Lmin->prev->next=Lmin->next;
if(Lmin->next)
Lmin->next->prev=Lmin->prev;
Lmin->next=Beg->next;
Lmin->prev=Beg;
Beg->next=Lmin;
if(Lmin->next)
Lmin->next->prev=Lmin;
}
}
}
Сортировка вставками:
---------------------
- аналог сортировки массива
void InsertSort(Link2* Start)
{
int buf,n=0;
Link2* Beg,*a,*b,*Beg1=new Link2;
Beg1->next=NULL;
Beg1->prev=NULL;
for(Beg=Start->next;Beg;Beg=a)
{
a=Beg->next;
for(b=Beg1;b->next;b=b->next)
if(b->next->Value>Beg->Value)
break;
Beg->next=b->next;
Beg->prev=b;
if(b->next)
b->next->prev=Beg;
b->next=Beg;
}
Start->next=Beg1->next;
Beg1->next->prev=Start;
delete Beg1;
}
- аналог предыдущей с циклом "while"
void InsertWSort(Link2* Start)
{
int buf,n=0;
Link2* Beg,*a,*b,*Beg1=new Link2;
Beg1->next=NULL;
Beg1->prev=NULL;
Beg=Start->next; // for(Beg=Start->next;Beg;Beg=a)
while(Beg)
{
a=Beg->next;
b=Beg1; // for(b=Beg1;b->next;b=b->next)
while(b->next)
{
if(b->next->Value>Beg->Value)
break;
b=b->next;
}
Beg->next=b->next;
Beg->prev=b;
if(b->next)
b->next->prev=Beg;
b->next=Beg;
Beg=a;
}
Start->next=Beg1->next;
Beg1->next->prev=Start;
delete Beg1;
}
Односвязный кольцевой список
================
struct Link1
{
int Value;
Link1* next;
};
кольцевой:
==========
Link1 *L1=new Link1;
L1->next=L1;
Вставка аналогична линейному списку.
Удаление:
void Delete(Link1* Pred)
{
Link1* Loc;
Loc=Pred->next;
Pred->next=Loc->next;
delete Loc;
}
Поиск:
int Search(Link1* Start,Link1*& Find,Link1*& Pred,int Key)
{
Link1* Cur=Start->next;
Pred=Start;
int Success=0;
while(Cur!=Start && !Success)
{
if(Cur->Value==Key)
{
Find=Cur;
Success=1;
break;
}
Pred=Cur;
Cur=Cur->next;
}
return Success;
}
Реверсирование списка
=====================
- с циклом "while"
void ReverseW(Link1* L)
{
Link1* a=L->next,*b=a,*c=L;
while(b!=L)
{
a=b;
b=a->next;
a->next=c;
c=a;
}
L->next=a;
}
Link1* ReverseW1(Link1* L)
{
Link1* a=L->next,*b,*c=L;
while(a!=L)
{
b=a->next;
a->next=c;
c=a;
a=b;
}
return c;
}
- с циклом "for"
void Reverse(Link1* L)
{
Link1* a=L->next,*b=a,*c=L;
for(;b!=L;a=b,b=a->next,a->next=c,c=a);
L->next=a;
}
Link1* Reverse1(Link1* L)
{
Link1* a=L->next,*b,*c=L;
for(;a!=L;b=a->next,a->next=c,c=a,a=b);
return c;
}
Сортировки
==========
Пузырьковая:
------------
- с процедурами дополнения и удаления
void BubbleListSort(Link1* Start)
{
int buf,n=0;
Link1* Last,*b,*b0;
for(Last=Start;Last!=Start->next;)
{
for(b0=Start,b=Start->next;b->next!=Last;b0=b0->next)
{
if(b->Value>b->next->Value)
{
buf=b->next->Value;
Delete(b);
Insert(b0,buf);
}
else
b=b->next;
}
Last=b;
}
}
- с заменой значений указателей
void Bubble2ListSort(Link1* Start)
{
int n=0;
Link1* Last,*b,*b0;
for(Last=Start;Last!=Start->next;)
{
for(b0=Start,b=Start->next;b->next!=Last;b0=b0->next)
{
if(b->Value>b->next->Value)
{
b0->next=b->next; // Перестановка звеньев
b->next=b->next->next;
b0->next->next=b;
}
else
b=b->next;
}
Last=b;
}
}
- с перемещением данных между звеньями
void BubbleListSortSimple(Link1* Start)
{
Link1* q;
int buf,n=0;
for(Link1* Last=Start,*e=Start->next;e->next!=Start;e=e->next)
{
for(q=Start->next;q->next!=Last;q=q->next)
{
if(q->Value>q->next->Value)
{
buf=q->Value;
q->Value=q->next->Value;
q->next->Value=buf;
}
}
Last=q;
}
}
Сортировка отбором:
-------------------
- аналог сортировки массива с процедурами дополнения и удаления
void SelectSort(Link1* Start)
{
int min,change,n=0;
Link1* Beg,*predmin,*b;
for(Beg=Start;Beg->next!=Start;Beg=Beg->next)
{
change=0;
min=Beg->next->Value;
for(b=Beg;b->next!=Start;b=b->next)
{
if(b->next->Value<min)
{
min=b->next->Value;
predmin=b;
change=1;
}
}
if(change)
{
Delete(predmin);
Insert(Beg,min);
}
}
}
Сортировка вставками:
---------------------
- аналог сортировки массива
void InsertSort(Link1* Start)
{
int buf,n=0;
Link1* Beg,*a,*b,*Beg1=new Link1;
Beg1->next=Start;
for(Beg=Start->next;Beg!=Start;Beg=a)
{
a=Beg->next;
for(b=Beg1;b->next!=Start;b=b->next)
if(b->next->Value>Beg->Value)
break;
Beg->next=b->next;
b->next=Beg;
}
Start->next=Beg1->next;
delete Beg1;
}
- аналог предыдущей с циклом "while"
void InsertWSort(Link1* Start)
{
int buf,n=0;
Link1* Beg,*a,*b,*Beg1=new Link1;
Beg1->next=Start;
Beg=Start->next; // for(Beg=Start->next;Beg;Beg=a)
while(Beg!=Start)
{
a=Beg->next;
b=Beg1; // for(b=Beg1;b->next;b=b->next)
while(b->next!=Start)
{
if(b->next->Value>Beg->Value)
break;
b=b->next;
}
Beg->next=b->next;
b->next=Beg;
Beg=a;
}
Start->next=Beg1->next;
delete Beg1;
}
двусвязный кольцевой список
================
struct Link2
{
int Value;
Link2* next,*prev;
};
кольцевой:
=========
Link2 *L2=new Link2;
L2->next=L2;
L2->prev=L2;
Добавление звена в произвольную позицию за ведущим звеном:
void Insert(Link2* Pred,int data)
{
Link2* Loc=new Link2;
Loc->Value=data;
Loc->next=Pred->next;
Loc->prev=Pred;
Pred->next=Loc;
Loc->next->prev=Loc;
}
Удаление звена из любого места списка за ведущим звеном:
void Delete(Link2* Del)
{
Del->prev->next=Del->next;
Del->next->prev=Del->prev;
delete Del;
}
Вывод содержимого списка в обратном порядке:
void ShowReverse(Link2* Start)
{
Link2* Loc=Start->prev;
while(Loc!=Start)
{
cout<<Loc->Value<<' ';
Loc=Loc->prev;
}
cout<<endl;
}
Поиск:
int Search(Link2* Start,Link2*& Find,int Key)
{
Link2* Cur=Start->next;
int Success=0;
while(Cur!=Start && !Success)
{
if(Cur->Value==Key)
{
Find=Cur;
Success=1;
break;
}
Cur=Cur->next;
}
return Success;
}
Реверсирование (обращение) списка
=================================
- с циклом "while"
void ReverseW(Link2* L)
{
Link2* a=L->next,*b=a,*c=L;
L->prev=a;
while(b!=L)
{
a=b;
b=a->next;
a->prev=b;
a->next=c;
c=a;
}
L->next=a;
}
Link2* ReverseW1(Link2* L)
{
Link2* a=L->next,*b,*c=L;
L->prev=a;
while(a!=L)
{
b=a->next;
a->prev=b;
a->next=c;
c=a;
a=b;
}
return c;
}
- с циклом "for"
void Reverse(Link2* L)
{
Link2* a=L->next;
L->prev=a;
for(Link2 *b=a,*c=L;b!=L;a=b,b=a->next,a->prev=b,a->next=c,c=a);
L->next=a;
}
Link2* Reverse1(Link2* L)
{
Link2* a=L->next,*c=L;
L->prev=a;
for(Link2 *b;a!=L;b=a->next,a->prev=b,a->next=c,c=a,a=b);
return c;
}
Сортировки
==========
Пузырьковая:
------------
- с процедурами удаления и дополнения
void BubbleListSort(Link2* Start)
{
int buf,n=0;
Link2* Last,*b,*b0;
for(Last=Start;Last!=Start->next;)
{
for(b0=Start,b=Start->next;b->next!=Last;b0=b0->next)
{
if(b->Value>b->next->Value)
{
buf=b->next->Value;
Delete(b->next);
Insert(b0,buf);
}
else
b=b->next;
}
Last=b;
}
}
- с заменой значений указателей
void Bubble2ListSort(Link2* Start)
{
int n=0;
Link2* Last,*b,*b0;
for(Last=Start;Last!=Start->next;)
{
for(b0=Start,b=Start->next;b->next!=Last;b0=b0->next)
{
if(b->Value>b->next->Value)
{
b0->next=b->next; // Перестановка звеньев // I
b->next->prev=b0;
b->next=b->next->next; // II
b->next->prev=b;
b0->next->next=b; // III
b->prev=b0->next;
}
else
b=b->next;
}
Last=b;
}
}
- с премещением данных между звеньями
void BubbleListSortSimple(Link2* Start)
{
Link2* q;
int buf,n=0;
for(Link2* Last=Start,*e=Start->next;e->next!=Start;e=e->next)
{
for(q=Start->next;q->next!=Last;q=q->next)
{
if(q->Value>q->next->Value)
{
buf=q->Value;
q->Value=q->next->Value;
q->next->Value=buf;
}
}
Last=q;
}
}
Сортировка отбором:
-------------------
- аналог сортировки массива с процедурами дополнения и удаления
void SelectSort(Link2* Start)
{
int min,change,n=0;
Link2* Beg,*Lmin,*b;
for(Beg=Start;Beg->next!=Start;Beg=Beg->next)
{
change=0;
min=Beg->next->Value;
for(b=Beg->next;b!=Start;b=b->next)
{
if(b->Value<min)
{
min=b->Value;
Lmin=b;
change=1;
}
}
if(change)
{
Delete(Lmin);
Insert(Beg,min);
}
}
}
Сортировка вставками:
---------------------
- аналог сортировки массива
void InsertSort(Link2* Start)
{
int buf,n=0;
Link2* Beg,*a,*b,*Beg1=new Link2;
Beg1->next=Start;
for(Beg=Start->next;Beg!=Start;Beg=a)
{
a=Beg->next;
for(b=Beg1;b->next!=Start;b=b->next)
if(b->next->Value>Beg->Value)
break;
Beg->next=b->next;
Beg->prev=b;
b->next->prev=Beg;
b->next=Beg;
}
Start->next=Beg1->next;
Beg1->next->prev=Start;
delete Beg1;
}
- аналог предыдущей с циклом "while"
void InsertWSort(Link2* Start)
{
int buf,n=0;
Link2* Beg,*a,*b,*Beg1=new Link2;
Beg1->next=Start;
Beg=Start->next; // for(Beg=Start->next;Beg;Beg=a)
while(Beg!=Start)
{
a=Beg->next;
b=Beg1; // for(b=Beg1;b->next;b=b->next)
while(b->next!=Start)
{
if(b->next->Value>Beg->Value)
break;
b=b->next;
}
Beg->next=b->next;
Beg->prev=b;
b->next->prev=Beg;
b->next=Beg;
Beg=a;
}
Start->next=Beg1->next;
Beg1->next->prev=Start;
delete Beg1;
}
пример обобщвющей программы на С++
#include <iostream>
using namespace std;
/*
Место размещения всех остальных функций
*/
int main()
{
int *mas=NULL; // указатель для создания динамического массива
int N; // размер массива
Link1 *L1=new Link2,*find,*cur;
L1->next=NULL;
int Key,i;
int Buf;
do
{
cout<<"1-Vvod 2-ProsmotrSpiska 3-Udalenie 4-Kopir 5-ProsmotrMassiva 6-Poisk 7-Sort 0-Vyhod"<<endl;
cin>>Key;
switch(Key)
{
case 1: cout<<"Vvedite dannye: "; cin>>Buf; Insert(L1,Buf); break;
case 2: cout<<"Spisok:"<<endl; ShowList(L1); break;
case 3: cout<<"Vvedite dannye dlja udalenija: "; cin>>Buf;
if(Search(L1,find,cur,Buf))
{
Delete(cur); ShowList(L1);
}
else cout<<"Dannye ne najdeny!"<<endl;
ShowList(L1);
break;
case 4:
if(mas)
delete[] mas;
N=ListSize(L1);
mas=new int [N];
CopyList(L1,mas);
ShowMas(mas,N);
break;
case 5: ShowMas(mas,N); break;
case 6: cout<<"Vvedite dannye: "; cin>>Buf;
i=Poisk2(mas,N,Buf);
if(i!=-1)
cout<<"Dannye najdeny v elemente "<<i<<endl;
else
cout<<"Dannyh net!"<<endl;
break;
case 7: select_sort(mas,N); ShowMas(mas,N); break;
}
}
while(Key);
return 0;
}
1. Что представляют собой связные списки?
2. К каким классификационным группам структур данных относятся списки?
3. Какие существуют разновидности связных списков?
4. В чем состоит отличие несвязного списка от массива?
5. В чем состоит отличие связного списка от массива?
6. В чем состоит отличие линейного списка от кольцевого?
7. В чем заключаются недостатки односвязного списка?
8. В чем состоит отличие односвязного списка от двусвязного?
9. Какие операции применяются для связных списков?
10. В чем отличие считывания информации из списка от считывания из очереди или стека?
11. Особенности операций вставки и удаления для связных списков.
12. В чем отличие операции вставки в двусвязный список от вставки в односвязный список?
13. В чем отличие операции удаления из двусвязного списка от удаления из односвязного списка?
14. В чем заключаются особенности работы с кольцевыми списками?
15. Какой тип должно иметь звено связного списка? Почему?
16. Что обязательно должно содержать звено связного списка?
17. В чем состоит отличие звена двусвязного списка от звена односвязного списка?
18. В чем состоит отличие связного списка от стека, организованного в виде связного списка?
19. Перечислите сходства и отличия списков и очередей.
20. Перечислите достоинства и недостатки линейных односвязных списков.
21. В чем заключается поиск в списке?
22. Изобразите структуру линейного односвязного списка.
23. Изобразите структуру линейного двусвязного списка.
24. Перечислите достоинства и недостатки линейных двусвязных списков.
25. Изобразите возможные структуры двусвязных кольцевых списков.
26. Объясните назначение заглавного звена в списках.
27. На каких структурах данных могут строится списки?
| Сколько полей содержит каждый элемент кольцевого двусвязного списка? | ||
| a) | ||
| b) | ||
| c) | ||
| d) | ||
| e) |
| Какие позиции списка с заглавным звеном доступны для занесения новых элементов? | ||
| a) | ||
| b) | ||
| c) | ||
| d) | ||
| e) |
| Какие операции над элементами характерны для списков? | ||
| a) | ||
| b) | ||
| c) | ||
| d) | ||
| e) |
| Какая структура данных имеет наименьший объем служебной информации? | ||
| a) | ||
| b) | ||
| c) | ||
| d) | ||
| e) |
| Сколько полей содержит каждый элемент линейного односвязного списка? | ||
| a) | ||
| b) | ||
| c) | ||
| d) | ||
| e) |
| Сколько полей содержит каждый элемент кольцевого односвязного списка? | ||
| a) | ||
| b) | ||
| c) | ||
| d) | ||
| e) |
| Из каких позиций списка с заглавным звеном можно удалять элементы? | ||
| a) | ||
| b) | ||
| c) | ||
| d) | ||
| e) |
| Из каких позиций списка можно извлекать элементы? | ||
| a) | ||
| b) | ||
| c) | ||
| d) | ||
| e) |
| Сколько полей содержит каждый элемент линейного двусвязного списка? | ||
| a) | ||
| b) | ||
| c) | ||
| d) | ||
| e) |
| Сколько полей содержит каждый элемент кольцевого двусвязного списка? | |
| Правильный ответ : | |
| 3. |
| Какие позиции списка с заглавным звеном доступны для занесения новых элементов? | |
| Правильный ответ : | |
| Все позиции, кроме заглавного звена |
| Какие операции над элементами характерны для списков? | |
| Правильный ответ : | |
| Занесение нового элемента в список, удаление элемента из списка, просмотр списка, поиск элемента в списке, сортировка списка. |
| Какая структура данных имеет наименьший объем служебной информации? | |
| Правильный ответ : | |
| Линейный односвязный список. |
| Сколько полей содержит каждый элемент линейного односвязного списка? | |
| Правильный ответ : | |
| 2. |
| Сколько полей содержит каждый элемент кольцевого односвязного списка? | |
| Правильный ответ : | |
| 2. |
| Из каких позиций списка с заглавным звеном можно удалять элементы? | |
| Правильный ответ : | |
| Из любой позиции, кроме заглавного звена. |
| Из каких позиций списка можно извлекать элементы? | |
| Правильный ответ : | |
| Из любой позиции. |
| Сколько полей содержит каждый элемент линейного двусвязного списка? | |
| Правильный ответ : | |
| 3. |
Выводы из данной статьи про связные списки на c указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое связные списки на c , pascal + тесты+ ы сортировки поиска вставки в списки и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных