Лекция
Привет, Вы узнаете о том , что такое адресация элементов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое адресация элементов, вектор айлиффа , настоятельно рекомендую прочитать все из категории Структуры данных.
1 Массив как логическая структура
2 . Массив как физическая структура
3. Операции над массивами
4. адресация элементов с помощью векторов Айлиффа
5 Примеры представления массивов с помощью векторов Айлиффа
В компьютерном программировании , вектор Айлиффа, также известный как дисплей , является структура данных , используется для реализации многомерных массивов . вектор айлиффа для n- мерного массива (где n ≥ 2) состоит из вектора (или 1-мерного массива) указателей на ( n - 1) -мерный массив. Они часто используются, чтобы избежать необходимости дорогостоящих операций умножения при выполнении вычисления адреса для элемента массива. Они также могут быть использованы для реализации зубчатых (рваных) массивов (Jagged array) , таких как треугольные массивы , треугольные матрицы и другие виды массивов неправильной формы. Структура данных названа в честь Джона К. Айлифф .(John K. Iliffe.)

Родился 18 сент 1931 лондон
К их недостаткам относится необходимость множественных косвенных указателей указателя для доступа к элементу и дополнительная работа, необходимая для определения следующей строки в n- мерном массиве, чтобы позволить оптимизирующему компилятору предварительно выбирать его. Оба они являются источником задержек в системах, где ЦП значительно быстрее основной памяти.
Вектор Айлиффа для двумерного массива - это просто вектор указателей на векторы данных, т.е. вектор Iliffe представляет столбцы массива, где каждый элемент столбца является указателем на вектор строки.
Многомерные массивы в таких языках, как Java , Python (многомерные списки), Ruby , Visual Basic .NET , Perl , PHP , JavaScript , Objective-C (при использовании NSArray, а не массива в стиле C для крупных строк ), Swift и Atlas Автокод реализован в виде векторов Айлиффа. Векторы Айлиффаиспользовались для реализации разреженных многомерных массивов в продукте OLAP Holos .
Векторы Айлиффа сравниваются с допинг-векторами (dope vectors ) в таких языках, как Fortran , которые содержат коэффициенты шага и значения смещения для индексов в каждом измерении. Вспомним основные понятия массивов
Массив - такая структура данных, которая характеризуется:
фиксированным набором элементов одного и того же типа;
Другое определение: массив - это вектор, каждый элемент которого - вектор.
Синтаксис описания массива представляется в виде:
< Имя > : Array [n1..k1] [n2..k2] .. Об этом говорит сайт https://intellect.icu . [nn..kn] of < Тип >.
Для случая двумерного массива:
Mas2D : Array [n1..k1] [n2..k2] of < Тип >, или
Mas2D : Array [n1..k1 , n2..k2] of < Тип >
Наглядно двумерный массив можно представить в виде таблицы из (k1-n1+1) строк и (k2-n2+1) столбцов.
Физическая структура - это размещение элементов массива в памяти ЭВМ. Для случая двумерного массива, состоящего из (k1-n1+1) строк и (k2-n2+1) столбцов физическая структура представлена на рис. 3.3.
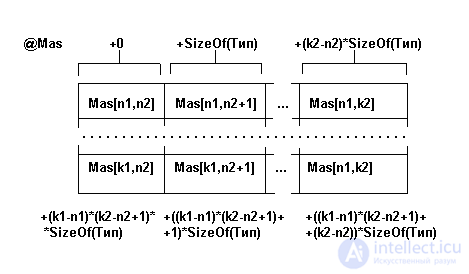
Рис. 3.3. Физическая структура двумерного массива из (k1-n1+1) строк и (k2-n2+1) столбцов
Многомерные массивы хранятся в непрерывной области памяти. Размер слота определяется базовым типом элемента массива. Количество элементов массива и размер слота определяют размер памяти для хранения массива. Принцип распределения элементов массива в памяти определен языком программирования. Так в FORTRAN элементы распределяются по столбцам - так, что быстрее меняется левые индексы, в PASCAL - по строкам - изменение индексов выполняется в направлении справа налево.
Количество байтов памяти, занятых двумерным массивом, определяется по формуле :
ByteSize = (k1-n1+1)*(k2-n2+1)*SizeOf(Тип)
Адресом массива является адрес первого байта начального компонента массива. Смещение к элементу массива Mas[i1,i2] определяется по формуле:
ByteNumber = [(i1-n1)*(k2-n2+1)+(i2-n2)]*SizeOf(Тип)
его адрес : @ByteNumber = @mas + ByteNumber.
Например:
var Mas : Array [3..5] [7..8] of Word;
Базовый тип элемента Word требует два байта памяти, тогда таблица 3.2 смещений элементов массива относительно @Mas будет следующей:
| Смещение (байт) | Идентификатор поля | Смещение (байт) | Идентификатор поля |
| + 0 | Mas[3,7] | + 2 | Mas[3,8] |
| + 4 | Mas[4,7] | +6 | Mas[4,8] |
| + 8 | Mas[5,7] | + 10 | Mas[5,8] |
Таблица 3.2
Этот массив будет занимать в памяти: (5-3+1)*(8-7+1)*2=12 байт; а адрес элемента Mas[4,8]:
@Mas+((4-3)*(8-7+1)+(8-7)*2 = @Mas+6
Важнейшая операция физического уровня над массивом - доступ к заданному элементу. Как только реализован доступ к элементу, над ним может быть выполнена любая операция, имеющая смысл для того типа данных, которому соответствует элемент. Преобразование логической структуры в физическую называется процессом линеаризации, в ходе которого многомерная логическая структура массива преобразуется в одномерную физическую структуру.
В соответствии с формулами (3.3), (3.4) и по аналогии с вектором (3.1), (3.2) для двумерного массива c границами изменения индексов:
[B(1)..E(1)][B(2)..E(2)], размещенного в памяти по строкам, адрес элемента с индексами [I(1),I(2)] может быть вычислен как:
Addr[I(1),I(2)] = Addr[B(1),B(2)] +
{ [I(1)-B(1)] * [E(2)-B(2)+1] + [I(2)-B(2)] }*SizeOf(Тип) (3.5)
Обобщая (3.5) для массива произвольной размерности:
Mas[B(1)..E(2)][B(2)..E(2)]...[B(n)..E(n)]
получим:
Addr[I(1),I(2),...,I(n)] = Addr[B(1),B(2),...B(n)] -
n n (3.6)
- Sizeof(Тип)*СУММА[B(m)*D(m)] + Sizeof(Тип)*СУММА[I(m)*D(m)]
m=1 m=1
где Dm зависит от способа размещения массива. При размещении по строкам:
D(m)=[E(m+1)-B(m+1)+1]*D(m+1), где m = n-1,...,1 и D(n)=1
при размещении по столбцам:
D(m)=[E(m-1)-B(m-1)+1]*D(m-1), где m = 2,...,n и D(1)=1
При вычислении адреса элемента наиболее сложным является вычисление третьей составляющей формулы (3.6), т.к. первые две не зависят от индексов и могут быть вычислены заранее. Для ускорения вычислений множители D(m) также могут быть вычислены заранее и сохраняться в дескрипторе массива. Дескриптор массива, таким образом, содержит:
Одно из определений массива гласит, что это вектор, каждый элемент которого - вектор. Некоторые языки программирования позволяют выделить из многомерного массива одно или несколько измерений и рассматривать их как массив меньшей мерности.
Например, если в PL/1-программе объявлен двумерный массив:
DECLARE A(10,10) BINARY FIXED;
то выражение: A[*,I] - будет обращаться к одномерному массиву, состоящему из элементов: A(1,I), A(2,I),...,A(10,I).
Символ-джокер "*" означает, что выбираются все элементы массива по тому измерению, которому соответствует заданный джокером индекс. Использование джокера позволяет также задавать групповые операции над всеми элементами массива или над выбранным его измерением,
например: A(*,I) = A(*,I) + 1
К операциям логического уровня над массивами необходимо отнести такие как сортировка массива, поиск элемента по ключу. Наиболее распространенные алгоритмы поиска и сортировок будут рассмотрены в данной главе ниже.
Из выше приведенных формул видно, что вычисление адреса элемента многомерного массива может потребовать много времени, поскольку при этом должны выполняться операции сложения и умножения, число которых пропорционально размерности массива. Операцию умножения можно исключить, если применять следующий метод.
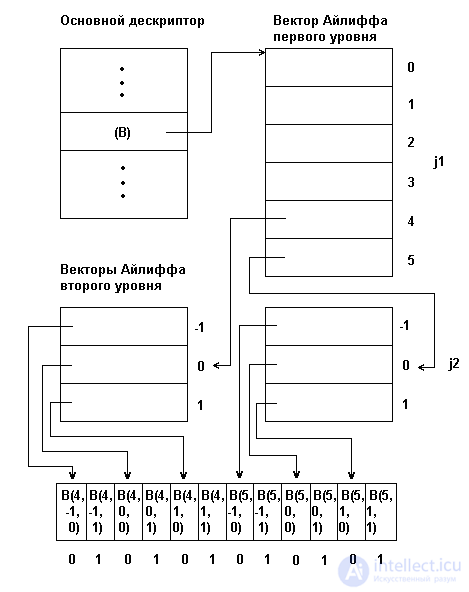
Рис. 3.4. Представление массивов с помощью векторов Айлиффа
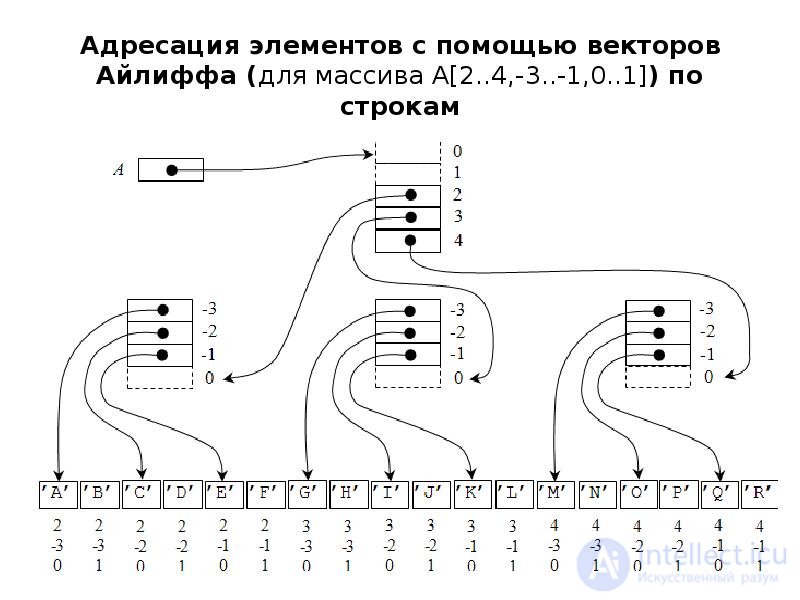
Для массива любой мерности формируется набор дескрипторов: основного и несколько уровней вспомогательных дескрипторов, называемых векторами Айлиффа. Каждый вектор Айлиффа определЯнного уровня содержит указатель на нулевые компоненты векторов Айлиффа следующего, более низкого уровня, а векторы Айлиффа самого нижнего уровня содержат указатели групп элементов отображаемого массива. Основной дескриптор массива хранит указатель вектора Айлиффа первого уровня. При такой организации к произвольному элементу В(j1,j2,...,jn) многомерного массива можно обратиться пройдя по цепочке от основного дескриптора через соответствующие компоненты векторов Айлиффа.
На рис. 3.4 приведена физическая структура трЯхмерного массива В[4..5,-1..1,0..1], представленная по методу Айлиффа. Из этого рисунка видно, что метод Айлиффа, увеличивая скорость доступа к элементам массива, приводит в то же время к увеличению суммарного объема памяти, требуемого для представления массива. В этом заключается основной недостаток представления массивов с помощью векторов Айлиффа.




Анализ данных, представленных в статье про адресация элементов, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое адресация элементов, вектор айлиффа и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных