Лекция
Привет, Вы узнаете о том , что такое вектор как структура данных, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое вектор как структура данных, представление вектора в памяти, хранение вектора в памяти , настоятельно рекомендую прочитать все из категории Структуры данных.
Вектор (одномерный массив) - структура данных с фиксированным числом элементов одного и того же типа типа. Каждый элемент вектора имеет уникальный в рамках заданного вектора номер. Обращение к элементу вектора выполняется по имени вектора и номеру требуемого элемента.
Элементы вектора размещаются в памяти в подряд расположенных ячейках памяти. Под элемент вектора выделяется количество байт памяти, определяемое базовым типом элемента этого вектора. Необходимое число байтов памяти для хранения одного элемента вектора называется слотом. Размер памяти для хранения вектора определяется произведением длины слота на число элементов.
В языках программирования вектор представляется одномерным массивом с синтаксисом описания вида (PASCAL):
< Имя > : array [n..k] of < тип >;
где n-номер первого элемента, k-номер последнего элемента. Представление в памяти вектора будет такое, как показано на рис. 1.

Рис. . представление вектора в памяти
где @ Имя -адрес вектора или, что тоже самое, адрес первого элемента вектора,
Sizeof(тип)-размер слота (количество байтов памяти для записи одного элемента вектора), (k-n)*Sizeof(тип) - относительный адрес элемента с номером k, или, что тоже самое, смещение элемента с номером k.
Например:
var m1:array[-2..2] of real;
представление данного вектора в памяти будет как на рис. 2.
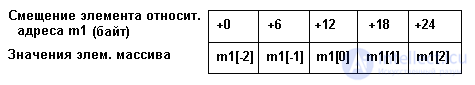
Рис. Об этом говорит сайт https://intellect.icu . 2. Представление вектора m1 в памяти
В языках, где память распределяется до выполнения программы на этапе компиляции (C, PASCAL, FORTRAN), при описании типа вектора граничные значения индексов должны определены. В языках, где память может распределяться динамически (ALGOL, PL/1), значения индексов могут быть заданы во время выполнения программы.
Количество байтов непрерывной области памяти, занятых одновременно вектором, определяется по формуле:
ByteSise = ( k - n + 1 ) * Sizeof (тип)
Обращение к i-тому элементу вектора выполняется по адресу вектора плюс смещение к данному элементу. Смещение i-ого элемента вектора определяется по формуле:
ByteNumer = ( i- n ) * Sizeof (тип),
а адрес его: @ ByteNumber = @ имя + ByteNumber.
где @ имя - адрес первого элемента вектора.
Например:
var МAS: array [ 5..10 ] of word.
Базовый тип элемента вектора - Word требует 2 байта, поэтому на каждый элемент вектора выделяется по два байта. Тогда таблица 1 смещений элементов вектора относительно @Mas выглядит так:
| Смещение (байт) | + 0 | + 2 | + 4 | + 6 | + 8 | + 10 |
| Идентификатор поля | MAS | MAS | MAS | MAS | MAS | MAS[10] |
Таблица 1
Этот вектор будет занимать в памяти: (10-5+1)*2 = 12 байт.
Смещение к элементу вектора с номером 8: (8-5)*2 = 6
Адрес элемента с номером 8: @ MAS + 6.
При доступе к вектору задается имя вектора и номер элемента вектора. Таким образом, адрес i-го элемента может быть вычислен как:
@Имя[i] = @Имя + i*Sizeof(тип) - n*Sizeof(тип) (3.1)
Это вычисление не может быть выполнено на этапе компиляции, так как значение переменной i в это время еще неизвестно. Следовательно, вычисление адреса элемента должно производиться на этапе выполнения программы при каждом обращении к элементу вектора. Но для этого на этапе выполнения, во-первых, должны быть известны параметры формулы (3.1): @Имя Sizeof(тип), n, а во-вторых, при каждом обращении должны выполняться две операции умножения и две - сложения. Преобразовав формулу (3.1) в формулу (3.2),
@Имя[i] = A0 + i*Sizeof(тип) -- (3.2)
A0 = @Имя - n*Sizeof(тип) --
сократим число хранимых параметров до двух, а число операций - до одного умножения и одного сложения, так как значение A0 может быть вычислено на этапе компиляции и сохранено вместе с Sizeof(тип) в дескрипторе вектора. Обычно в дескрипторе вектора сохраняются и граничные значения индексов. При каждом обращении к элементу вектора заданное значение сравнивается с граничными и программа аварийно завершается, если заданный индекс выходит за допустимые пределы.
Таким образом, информация, содержащаяся в дескрипторе вектора, позволяет, во-первых, сократить время доступа, а во-вторых, обеспечивает проверку правильности обращения. Но за эти преимущества приходится платить, во-первых, быстродействием, так как обращения к дескриптору - это команды, во-вторых, памятью как для размещения самого дескриптора, так и команд, с ним работающих.
Можно ли обойтись без дескриптора вектора?
В языке C, например, дескриптор вектора отсутствует, точнее, не сохраняется на этапе выполнения. Индексация массивов в C обязательно начинается с нуля. Компилятор каждое обращение к элементу массива заменяет на последовательность команд, реализующую частный случай формулы (3.1) при n = 0:
@Имя[i] = @Имя + i*Sizeof(тип)
Программисты, привыкшие работать на C, часто вместо выражения вида: Имя[i] употребляют выражение вида: *(Имя+i).
Но во-первых, ограничение в выборе начального индекса само по себе может являться неудобством для программиста, во-вторых, отсутствие граничных значений индексов делает невозможным контроль выхода за пределы массива. Программисты, работающие с C, хорошо знают, что именно такие ошибки часто являются причиной "зависания" C-программы при ее отладке.
Исследование, описанное в статье про вектор как структура данных, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое вектор как структура данных, представление вектора в памяти, хранение вектора в памяти и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Из статьи мы узнали кратко, но содержательно про вектор как структура данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных