6.2 Сортировка методом прямого выбора, и методом выбора кратко

Привет, сегодня поговорим про сортировка выбором, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое сортировка выбором, сортировка методом выбора, сортировка методом прямого выбора , настоятельно рекомендую прочитать все из категории Структуры данных.

сортировка выбором

Сортировка выбором – возможно, самый простой в реализации алгоритм сортировки. Как и в большинстве других подобных алгоритмов, в его основе лежит операция сравнения. Сравнивая каждый элемент с каждым, и в случае необходимости производя обмен, метод приводит последовательность к необходимому упорядоченному виду.

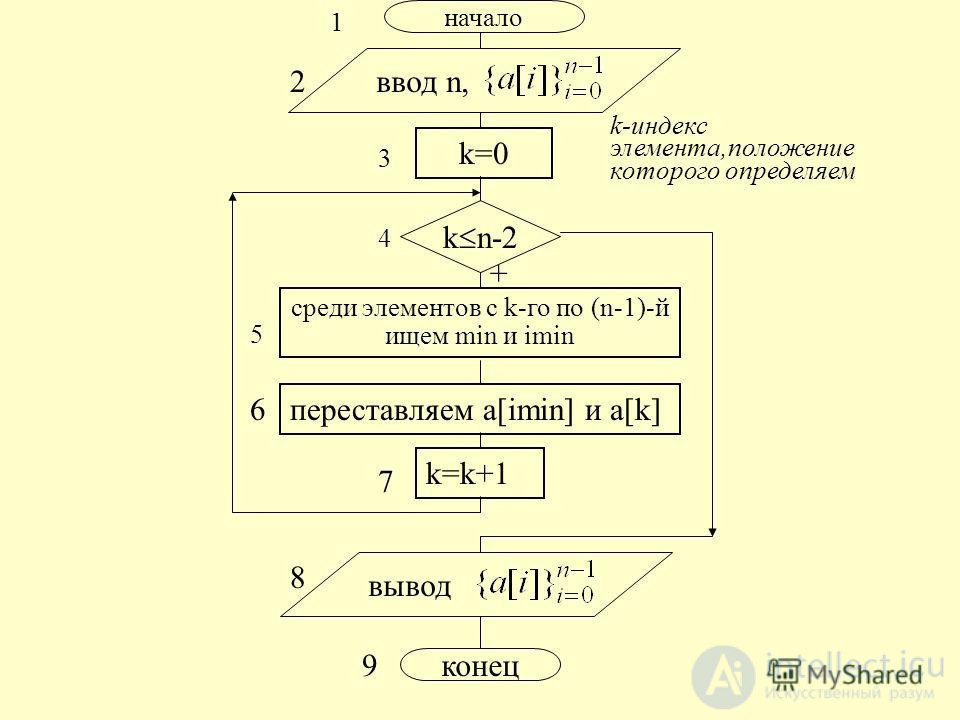
Идея алгоритма очень проста. Пусть имеется массив A размером N, тогда сортировка выбором сводится к следующему:

1. берем первый элемент последовательности A[i], здесь i – номер элемента, для первого i равен 1;
2. находим минимальный (максимальный) элемент последовательности и запоминаем его номер в переменную key;
3. если номер первого элемента и номер найденного элемента не совпадают, т. е. если key≠1, тогда два этих элемента обмениваются значениями, иначе никаких манипуляций не происходит;
4. увеличиваем i на 1 и продолжаем сортировку оставшейся части массива, а именно с элемента с номером 2 по N, так как элемент A уже занимает свою позицию;

С каждым последующим шагом размер подмассива, с которым работает алгоритм, уменьшается на 1, но на способ сортировки это не влияет, он одинаков для каждого шага.

Рассмотрим работу алгоритма на примере конкретной последовательности целых чисел. Дан массив, состоящий из пяти целых чисел 9, 1, 4, 7, 5 (см. рис.). Требуется расположить его элементы по возрастанию, используя сортировку выбором. Начнем по порядку сравнивать элементы. Второй элемент меньше первого – запоминаем это (key=2). Далее мы видим, что он также меньше и всех остальных, а так как key≠1, меняем местами первый и второй элементы. Продолжим упорядочивание оставшейся части, пытаясь найти замену элементу со значением 9. Теперь в key будет занесена 3-ка, поскольку элемент с номером 3 имеет наименьшее значение. Как видно, key≠2, следовательно, меняем местами 2-ой и 3-ий элементы. Продолжаем расставлять на места элементы, пока на очередном шаге размер поддмассива не станет равным 1-ому.

Код программы на C++:

Код программы на Pascal:

Сортировка выбором проста в реализации, и в некоторых ситуациях стоит предпочесть ее наиболее сложным и совершенным методам. Об этом говорит сайт https://intellect.icu . Но в большинстве случаев данный алгоритм уступает в эффективности последним, так как в худшем, лучшем и среднем случае ей потребуется О(n²) времени

сортировка методом прямого выбора

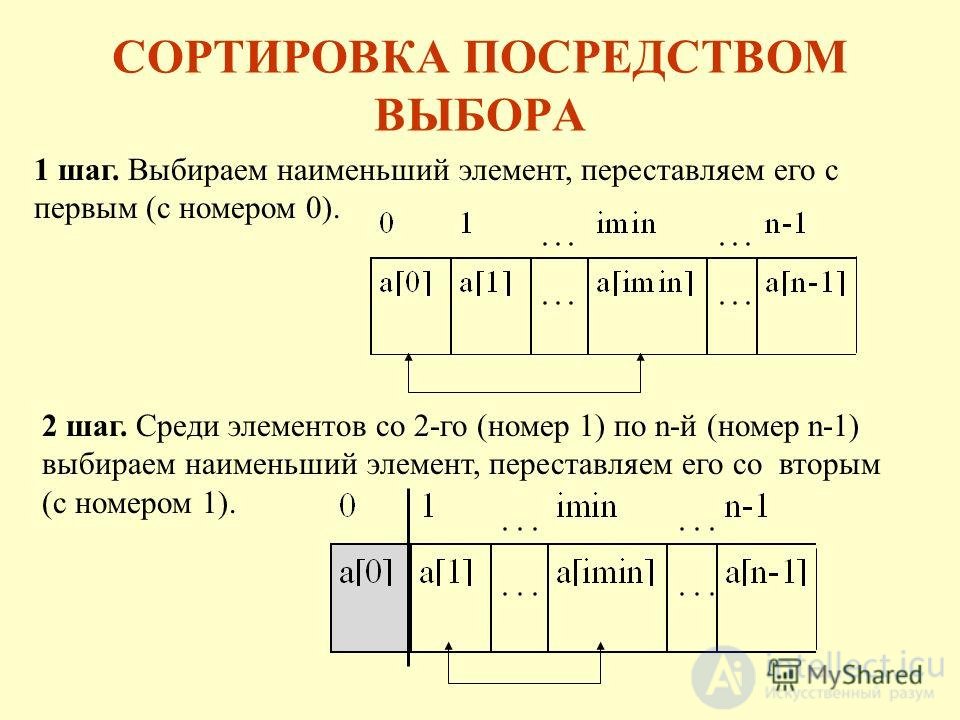
Прием сортировка методом прямого выбора основан на следующих принципах:

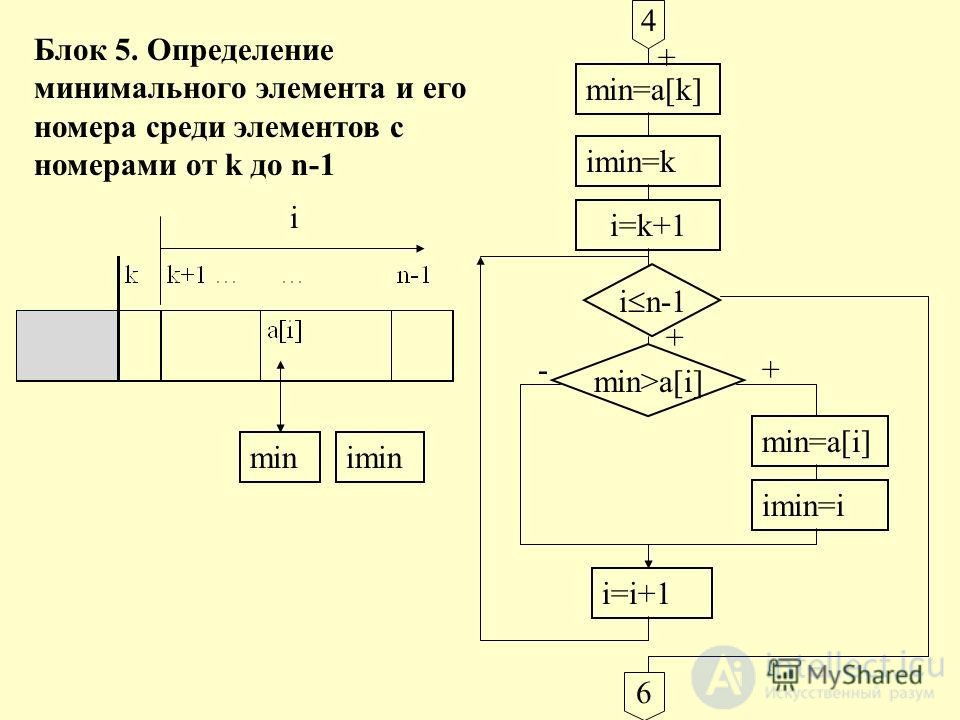
1. Выбирается элемент с наименьшим ключом.

2. Он меняется местами с первым элементом a ₁.

3. Затем этот процесс повторяется с оставшимися n-1 элементами, n-2 элементами и т.д. до тех пор, пока не останется один, самый "большой" элемент.

Алгоритм формулируется так:

for i = 1 to n - 1 x = a(i) k = i for j = i + 1 to n if a(j) < x then k = j x = a(k) endif next j a(k) = a(i) a(i) = x next i return

for i := 1 to n - 1 do begin x := a[i]; k := i; for j := i + 1 to n do if a[j] < x then begin k := j; x := a[k]; end; a[k] := a[i]; a[i] := x; end;

Эффективность алгоритма:

Число сравнений ключей C, очевидно, не зависит от начального порядка ключей. Можно сказать, что в этом смысле поведение этого метода менее естественно, чем поведение прямого включения. Для C при любом расположении ключей имеем:

C = n(n-1)/2

Порядок числа сравнений, таким образом, О(n²)

Число перестановок минимально М_min = 3(n - 1) в случае изначально упорядоченных ключей и максимально, М_max = 3(n - 1) + С, т.е. порядок О(n²), если первоначально ключи располагались в обратном порядке.

В худшем случае сортировка прямым выбором дает порядок n², как для числа сравнений, так и для числа перемещений.

Сортировка посредством выбора

При сортировке посредством выбора из массива выбирается элемент с наименьшим значением и обменивается с первым элементом. Затем из оставшихся n - 1 элементов снова выбирается элемент с наименьшим ключом и обменивается со вторым элементом, и т.д. Эти обмены продолжаются до двух последних элементов. Например, если применить метод выбора к массиву dcab, каждый проход будет выглядеть так, как показано ниже:

Начало       d c a b
Проход 1     a c d b
Проход 2     a b d c
Проход 3     a b c d

Нижеследующий код демонстрирует простейшую сортировку посредством выбора:

/* Сортировка посредством выбора. */
void select(char *items, int count)
{
  register int a, b, c;
  int exchange;
  char t;

  for(a=0; a < count-1; ++a) {
    exchange = 0;
    c = a;
    t = items[a];
    for(b=a+1; b < count; ++b) {
      if(items[b] < t) {
        c = b;
        t = items[b];
        exchange = 1;
      }
    }
    if(exchange) {
      items[c] = items[a];
      items[a] = t;
    }
  }
}

К сожалению, как и в пузырьковой сортировке, внешний цикл выполняется n - 1 раз, а внутренний — в среднем n/2 раз. Следовательно, сортировка посредством выбора требует

1/2(n2-n)

сравнений. Таким образом, это алгоритм порядка n2, из-за чего он считается слишком медленным для сортировки большого количества элементов. Несмотря на то, что количество сравнений в пузырьковой сортировке и сортировке посредством выбора одинаковое, в последней количество обменов в среднем случае намного меньше, чем в пузырьковой сортировке.

Называется также сортировкой выбором и сортировкой выборками.

Число сравнений при сортировке с посредством выбора

Electron in the transistor-resistor kingdom

Game: Perform tasks and rest cool.6 people play!

Play game

Вау!! 😲 Ты еще не читал? Это зря!:

• алгоритмы сортировки , сортировка , сортировка пузырьком , bubble sort ,
• сортировка шелла ,
• Шейкерная сортировка (перемешиванием) .
• Сортировка слиянием .
• Сортировка пузырьком .
• Быстрая сортировка .
• Сортировка выбором .

Алгоритмы сортировки
Теория	Сложность О-нотация Отношение порядка Типы сортировки Устойчивая Внутренняя Внешняя
Обменные	Сортировка пузырьком , Сортировка перемешиванием , Сортировка гномья, Сортировка быстрая, Сортировка расческой , Сортировка чет-нечет , Сортировка поразрядная
Выбором	Сортировка выбором , Сортировка пирамидальная, Сортировка плавная
Вставками	Сортировка вставками , Сортировка Шелла , Сортировка деревом
Слиянием	Сортировка cлиянием
Без сравнений	Сортировка подсчетом , Сортировка блочная
Гибридные	Сортировка Introsort, Сортировка Timsort
Прочее	Сортировка Топологическая , Сортировка сети, Сортировка Битонная
Непрактичные	Сортировка Bogosort, Сортировка Stooge sort , Сортировка Блинная, медленная сортировка

Electron in the transistor-resistor kingdom

Game: Perform tasks and rest cool.6 people play!

Play game

На этом все! Теперь вы знаете все про сортировка выбором, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое сортировка выбором, сортировка методом выбора, сортировка методом прямого выбора и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных