Лекция
Привет, Вы узнаете о том , что такое приоритетная очередь, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое приоритетная очередь, очередь с приоритетом, параллельная приоритетная очередь , настоятельно рекомендую прочитать все из категории Структуры данных.
очередь с приоритетом (англ. priority queue) — абстрактный тип данных в программировании, поддерживающий две обязательные операции — добавить элемент и извлечь максимум (минимум). Предполагается, что для каждого элемента можно вычислить его приоритет — действительное число или в общем случае элемент линейно упорядоченного множества.
Основные методы, реализуемые очередью с приоритетом, следующие:
При этом меньшее значение ключа соответствует более высокому приоритету.
В некоторых случаях более естественен рост ключа вместе с приоритетом. Тогда второй метод можно назвать extract_maximum().
Есть ряд реализаций, в которых обе основные операции выполняются в худшем случае за время, ограниченное O(logn) (см. «O» большое и «o» малое), где n — количество хранимых пар.
приоритетная очередь должна как минимум поддерживать следующие операции:
Это также известно как « pop_element(Off) », « get_maximum_element » или « get_front(most)_element ».
Некоторые соглашения меняют порядок приоритетов на обратный, считая более низкие значения более приоритетными, поэтому это также может быть известно как « get_minimum_element », а в литературе часто упоминается как « get-min ».
Вместо этого это можно указать как отдельные функции « peek_at_highest_priority_element » и « delete_element », которые можно объединить для получения « pull_highest_priority_element ».
Кроме того, peek (в этом контексте часто называемый find-max или find-min ), который возвращает элемент с наивысшим приоритетом, но не изменяет очередь, очень часто реализуется и почти всегда выполняется за время O (1) . Эта операция и ее производительность O (1) имеют решающее значение для многих приложений приоритетных очередей.
Более продвинутые реализации могут поддерживать более сложные операции, такие как pull_lowest_priority_element , проверку первых нескольких элементов с наивысшим или наименьшим приоритетом, очистку очереди, очистку подмножеств очереди, выполнение пакетной вставки, объединение двух или более очередей в одну, увеличение приоритета любого элемента и т. д.
Стеки и очереди могут быть реализованы как особые виды очередей приоритетов, где приоритет определяется порядком, в котором вставляются элементы. В стеке приоритет каждого вставленного элемента монотонно увеличивается; таким образом, последний вставленный элемент всегда извлекается первым. В очереди приоритет каждого вставленного элемента монотонно уменьшается; таким образом, первый вставленный элемент всегда извлекается первым.
В качестве примера очереди с приоритетом можно рассмотреть список задач работника. Когда он заканчивает одну задачу, он переходит к очередной — самой приоритетной (ключ будет величиной, обратной приоритету) — то есть выполняет операцию извлечения максимума. Начальник добавляет задачи в список, указывая их приоритет, то есть выполняет операцию добавления элемента.
На практике интерфейс очереди с приоритетом нередко расширяют другими операциям:
В индексированных очередях с приоритетом (адресуемых) возможно обращение к элементам по индексу. Такие очереди могут быть использованы, например, для слияния нескольких отсортированных последовательностей (multiway merge).
Могут также рассматриваться очереди с приоритетом с двусторонним доступом (англ. double-ended priority queue, DEPQ), в которых есть операции доступа как к минимальному, так и к максимальному элементу.
Очередь с приоритетами может быть реализована на основе различных структур данных.
Простейшие (и не очень эффективные) реализации могут использовать неупорядоченный или упорядоченный массив, связный список, подходящие для небольших очередей. При этом вычисления могут быть как «ленивыми» (тяжесть вычислений переносится на извлечение элемента), так и ранними (eager), когда вставка элемента сложнее его извлечения. То есть, одна из операций может быть произведена за время O(1), а другая — в худшем случае за O(N), где N — длина очереди.
Более эффективными являются реализации на основе кучи, где обе операции можно производить в худшем случае за время O(logN). К ним относятся двоичная куча, биномиальная куча, фибоначчиева куча, pairing heap.
Абстрактный тип данных (АТД) для очереди с приоритетом получается из АТД кучи переименованием соответствующих функций. Минимальное (максимальное) значение находится всегда на вершине кучи.
Стандартная библиотека Python содержит модуль heap, реализующий очередь с приоритетом:
# импорт двух функций очереди под именами, принятыми в данной статье
from heapq import heappush as insert, heappop as extract_maximum
pq = [] # инициализация списка
insert(pq, (4, 0, "p")) # вставка в очередь элемента "p" с индексом 0 и приоритетом 4
insert(pq, (2, 1, "e"))
insert(pq, (3, 2, "a"))
insert(pq, (1, 3, "h"))
# вывод четырех элементов в порядке возрастания приоритетов
print(extract_maximum(pq)[-1] + extract_maximum(pq)[-1] + extract_maximum(pq)[-1] + extract_maximum(pq)[-1])
Этот пример выведет слово «heap».
Приоритетная очередь может использоваться для управления ограниченными ресурсами, такими как полоса пропускания на линии передачи от сетевого маршрутизатора . В случае возникновения очереди исходящего трафика из-за недостаточной пропускной способности все остальные очереди могут быть остановлены для отправки трафика из очереди с наивысшим приоритетом по прибытии. Это гарантирует, что приоритетный трафик (такой как трафик в реальном времени, например, поток RTP VoIP- соединения) будет пересылаться с наименьшей задержкой и наименьшей вероятностью отклонения из-за достижения очередью максимальной емкости. Весь остальной трафик может обрабатываться, когда очередь с наивысшим приоритетом пуста. Другой используемый подход заключается в отправке непропорционально большего количества трафика из очередей с более высоким приоритетом.
Многие современные протоколы для локальных сетей также включают концепцию приоритетных очередей на подуровне управления доступом к среде (MAC), чтобы гарантировать, что высокоприоритетные приложения (такие как VoIP или IPTV ) испытывают меньшую задержку, чем другие приложения, которые могут обслуживаться с наилучшими усилиями . Примерами являются IEEE 802.11e (поправка к IEEE 802.11 , которая обеспечивает качество обслуживания ) и ITU-T G.hn (стандарт для высокоскоростной локальной сети , использующей существующую домашнюю проводку ( линии электропередач , телефонные линии и коаксиальные кабели ).
Обычно ограничение (policer) устанавливается для ограничения полосы пропускания, которую может занять трафик из очереди с наивысшим приоритетом, чтобы не допустить, чтобы пакеты с высоким приоритетом перекрывали весь остальной трафик. Этот предел обычно никогда не достигается из-за высокоуровневых контрольных экземпляров, таких как Cisco Callmanager , который можно запрограммировать на блокировку вызовов, которые могут превысить запрограммированный предел полосы пропускания.
Другое применение приоритетной очереди — управление событиями в дискретном моделировании событий . События добавляются в очередь, а время их моделирования используется в качестве приоритета. Выполнение моделирования происходит путем многократного вытягивания вершины очереди и выполнения события на ней.
См. : Планирование (вычисления) , теория очередей
Если граф хранится в виде списка смежности или матрицы, то для эффективного извлечения минимума при реализации алгоритма Дейкстры можно использовать приоритетную очередь , хотя также необходима возможность эффективно изменять приоритет конкретной вершины в приоритетной очереди.
Если вместо этого граф хранится как объекты узлов, а пары приоритет-узел вставляются в кучу, изменение приоритета конкретной вершины не требуется, если отслеживаются посещенные узлы. После посещения узла, если он снова появляется в куче (имея ранее связанный с ним более низкий номер приоритета), он выталкивается и игнорируется.
Кодирование Хаффмана требует многократного получения двух деревьев с самой низкой частотой. Приоритетная очередь — один из методов сделать это .
Алгоритмы поиска «лучший первый» , такие как алгоритм поиска A* , находят кратчайший путь между двумя вершинами или узлами взвешенного графа , пробуя сначала наиболее перспективные маршруты. Очередь приоритетов (также известная как fringe ) используется для отслеживания неисследованных маршрутов; тот, для которого оценка (нижняя граница в случае A*) общей длины пути наименьшая, получает наивысший приоритет. Если ограничения памяти делают поиск «лучший первый» непрактичным, вместо него можно использовать варианты, такие как алгоритм SMA* , с двухсторонней очередью приоритетов, чтобы разрешить удаление элементов с низким приоритетом.
Алгоритм Real-time Optimally Adapting Meshes ( ROAM ) вычисляет динамически изменяющуюся триангуляцию рельефа. Он работает путем разделения треугольников, где требуется больше деталей, и их объединения, где требуется меньше деталей. Алгоритм назначает каждому треугольнику на рельефе приоритет, обычно связанный с уменьшением ошибки, если бы этот треугольник был разделен. Алгоритм использует две очереди приоритетов, одну для треугольников, которые можно разделить, и другую для треугольников, которые можно объединить. На каждом шаге треугольник из очереди разделения с наивысшим приоритетом разделяется, или треугольник из очереди слияния с наименьшим приоритетом объединяется со своими соседями.
Используя очередь приоритета min heap в алгоритме Прима для поиска минимального остовного дерева связного и неориентированного графа , можно добиться хорошего времени выполнения. Эта очередь приоритета min heap использует структуру данных min heap, которая поддерживает такие операции, как вставка , минимум , извлечение минимума , уменьшение ключа . В этой реализации вес ребер используется для определения приоритета вершин . Чем меньше вес, тем выше приоритет, а чем больше вес, тем ниже приоритет.
Распараллеливание может быть использовано для ускорения приоритетных очередей, но требует некоторых изменений в интерфейсе приоритетной очереди. Причина таких изменений в том, что последовательное обновление обычно имеет только или
стоимость, и нет практической выгоды от распараллеливания такой операции. Об этом говорит сайт https://intellect.icu . Одно из возможных изменений — разрешить одновременный доступ нескольких процессоров к одной и той же очереди приоритетов. Второе возможное изменение — разрешить пакетные операции, которые работают на k элементов, а не только одного элемента. Например, extractMin удалит первый k элементы с наивысшим приоритетом.
Если приоритетная очередь допускает параллельный доступ, несколько процессов могут выполнять операции параллельно в этой приоритетной очереди. Однако это поднимает две проблемы. Во-первых, определение семантики отдельных операций больше не очевидно. Например, если два процесса хотят извлечь элемент с наивысшим приоритетом, должны ли они получить один и тот же элемент или разные? Это ограничивает параллелизм на уровне программы, использующей приоритетную очередь. Кроме того, поскольку несколько процессов имеют доступ к одному и тому же элементу, это приводит к конкуренции.
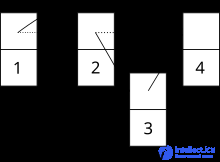
Узел 3 вставляется и устанавливает указатель узла 2 на узел 3. Сразу после этого узел 2 удаляется, а указатель узла 1 устанавливается на узел 4. Теперь узел 3 больше недоступен.
Параллельный доступ к приоритетной очереди может быть реализован на модели PRAM Concurrent Read, Concurrent Write (CRCW). В дальнейшем приоритетная очередь реализована как список пропусков . Кроме того, примитив атомарной синхронизации CAS используется для того, чтобы сделать список пропусков неблокируемым . Узлы списка пропусков состоят из уникального ключа, приоритета, массива указателей для каждого уровня на следующие узлы и метки удаления . Метка удаления отмечает, что узел собирается быть удаленным процессом. Это гарантирует, что другие процессы смогут соответствующим образом отреагировать на удаление.
Если разрешен одновременный доступ к приоритетной очереди, между двумя процессами могут возникнуть конфликты. Например, конфликт возникает, если один процесс пытается вставить новый узел, но в то же время другой процесс собирается удалить предшественника этого узла. Существует риск того, что новый узел будет добавлен в список пропускаемых, но он больше не будет доступен. ( См. изображение )
В настройках разделяемой памяти параллельная приоритетная очередь может быть легко реализована с использованием параллельных двоичных деревьев поиска и алгоритмов дерева на основе объединения . В частности, k_extract-min соответствует разделению на двоичном дереве поиска, которое имеет стоимость и дает дерево, которое содержит k наименьшие элементы. k_insert может быть применен путем объединения исходной очереди приоритетов и пакета вставок. Если пакет уже отсортирован по ключу, k_insert имеет
стоимость. В противном случае нам нужно сначала отсортировать партию, поэтому стоимость будет
. Другие операции для очереди приоритетов могут быть применены аналогичным образом. Например, k_decrease-key может быть выполнен путем применения сначала разности , а затем объединения , которое сначала удаляет элементы, а затем вставляет их обратно с обновленными ключами. Все эти операции высокопараллельны, а теоретическую и практическую эффективность можно найти в соответствующих исследовательских работах.
Остальная часть этого раздела посвящена алгоритму на основе очередей в распределенной памяти. Мы предполагаем, что каждый процессор имеет свою собственную локальную память и локальную (последовательную) приоритетную очередь. Элементы глобальной (параллельной) приоритетной очереди распределены по всем процессорам.
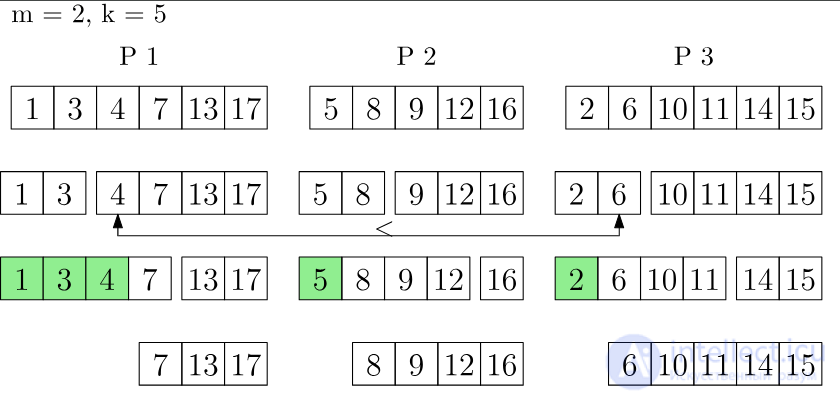
k_extract-min выполняется в приоритетной очереди с тремя процессорами. Зеленые элементы возвращаются и удаляются из приоритетной очереди.
Операция k_insert назначает элементы равномерно случайным образом процессорам, которые вставляют элементы в свои локальные очереди. Обратите внимание, что отдельные элементы все еще могут быть вставлены в очередь. При использовании этой стратегии глобальные наименьшие элементы находятся в объединении локальных наименьших элементов каждого процессора с высокой вероятностью. Таким образом, каждый процессор удерживает репрезентативную часть глобальной приоритетной очереди.
Это свойство используется при выполнении k_extract-min , как наименьшее m Элементы каждой локальной очереди удаляются и собираются в набор результатов. Элементы в наборе результатов по-прежнему связаны с их исходным процессором. Количество элементов m который удаляется из каждой локальной очереди, зависит от k и количество процессоров p . Параллельным отбором k Определяются наименьшие элементы результирующего набора. С большой вероятностью это глобальные k наименьшие элементы. Если нет, m элементы снова удаляются из каждой локальной очереди и помещаются в результирующий набор. Это делается до тех пор, пока глобальный k Наименьшие элементы находятся в результирующем наборе. Теперь эти k элементы могут быть возвращены. Все остальные элементы набора результатов вставляются обратно в свои локальные очереди. Время выполнения k_extract-min ожидается , где
и n размер приоритетной очереди.
Очередь приоритетов можно дополнительно улучшить, не перемещая оставшиеся элементы набора результатов напрямую обратно в локальные очереди после операции k_extract-min . Это экономит перемещение элементов туда и обратно все время между набором результатов и локальными очередями.
Удаляя несколько элементов сразу, можно достичь значительного ускорения. Но не все алгоритмы могут использовать этот тип очереди приоритетов. Например, алгоритм Дейкстры не может работать на нескольких узлах одновременно. Алгоритм берет узел с наименьшим расстоянием от очереди приоритетов и вычисляет новые расстояния для всех его соседних узлов. Если бы вы убрали k узлы, работая на одном узле, можно изменить расстояние до другого узла k узлы. Таким образом, использование операций с k-элементами разрушает свойство установки меток алгоритма Дейкстры.
Исследование, описанное в статье про приоритетная очередь, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое приоритетная очередь, очередь с приоритетом, параллельная приоритетная очередь и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных