Лекция
Привет, сегодня поговорим про поиск данных, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое поиск данных, последовательный поиск, индексно-последовательный поиск, алгоритмы поиска, логарифмический поиск, бинарный поиск, метод делением пополам, сравнение алгоритмов поиска , настоятельно рекомендую прочитать все из категории Структуры данных.
поиск данных — раздел информатики, изучающий алгоритмы для поиска и обработки информации как в структурированных (см. напр. базы данных) так и неструктурированных (напр., текстовый документ) данных. Поиск данных неразрывно связан с понятием фильтрации данных.
Поиск данных является одной из основных операций при обработке информации на компьютере. Ее назначение - по заданному аргументу найти среди массива данных те данные, которые соответствуют этому аргументу.
Набор данных (любых) будем называть таблицей или файлом. Любое данное (или элемент структуры) отличается каким-то признаком от других данных. Этот признак называется ключом. Ключ может быть уникальным, т. е. в таблице существует только одно данное с этим ключом. Такой уникальный ключ называется первичным. Вторичный ключ в одной таблице может повторяться, но по нему тоже можно организовать поиск. Ключи данных могут быть собраны в одном месте (в другой таблице) или представлять собой запись, в которой одно из полей - это ключ. Ключи, которые выделены из таблицы данных и организованы в свой файл, называются внешними ключами. Если ключ находится в записи, то он называется внутренним.
Задача поиска связана с нахождением заданного значения, называется ключом поиска (search key) среди заданного множества (или мультимножества). Существует огромное количество алгоритмов поиска. Их сложность варьируется от простых алгоритмов поиска методом последовательного сравнения, в чрезвычайно эффективных, но ограниченных алгоритмов бинарного поиска, а также алгоритмов, основанных на представлении базовой множества в другой, более подходящей для поиска форме. Последние из упомянутых алгоритмов имеют особое практическое значение, поскольку применяются в реально действующих приложениях, выполняющих выбор и хранения массивов информации в огромных базах данных.
Для решения задачи поиска также не существует единого алгоритма, который бы лучше подходил для всех случаев. Некоторые из алгоритмов выполняются быстрее других, но для их работы требуется дополнительная оперативная память. Другие выполняются очень быстро, но их можно применять только для заранее отсортированных массивов и тому подобное. В отличие от алгоритмов сортировки, в алгоритмах поиска нет проблемы устойчивости, но при их использовании могут возникать другие сложности. В частности, в тех приложениях, где обрабатываемые данные могут меняться, причем количество изменений сопоставима с количеством операций поиска, поиск следует рассматривать в неразрывной связи с двумя другими операциями - добавление элемента в набор данных и удаления из него. В подобных ситуациях необходимо видоизменить структуры данных и алгоритмы так, чтобы достигалась равновесие между требованиями, предъявляемыми к каждой операции. Кроме того, организация очень больших наборов данных с целью выполнения в них эффективного поиска (а также добавление и удаление элементов) является чрезвычайно сложной задачей, решение которой особенно важно с точки зрения практического применения.
Одними из важнейших процедур обработки структурированной информации является поиск. Задача поиска привлекала большое внимание ученых (программистов) еще на заре компьютерной эры. С 50-х годов началось решение проблемы поиска элементов, обладающих определенным свойством в заданном множестве. Алгоритмам поиска посвятили свои труды J. von Neumann, K. E. Batcher, J. W. J. Williams, R. W. Floyd, R. Sedgewick, E. J. Isaac, C. A. R. Hoare, D. E. Knuth, R. C. Singleton, D. L. Shell и другие. Исследования алгоритмов поиска ведутся и в настоящее время.
У каждого алгоритма есть свои преимущества и недостатки. Поэтому важно выбрать тот алгоритм, который лучше всего подходит для решения конкретной задачи.
Задачу поиска можно сформулировать так: найти один или несколько элементов в множестве, причем искомые элементы должны обладать определенным свойством. Это свойство может быть абсолютным или относительным. Относительное свойство характеризует элемент по отношению к другим элементам: например, минимальный элемент в множестве чисел. Пример задачи поиска элемента с абсолютным свойством: найти в конечном множестве занумерованных элементов элемент с номером 13, если такой существует.
Таким образом, в задаче поиска имеются следующие шаги :
1) вычисление свойства элемента; часто это - просто получение «значения» элемента, ключа элемента и т. д.;
2) сравнение свойства элемента с эталонным свойством (для абсолютных свойств) или сравнение свойств двух элементов (для относительных свойств);
3) перебор элементов множества, т. е. прохождение по элементам множества.
Первые два шага относительно просты. Вся суть различных методов поиска сосредоточена в методах перебора, в стратегии поиска и здесь возникает ряд вопросов :
Ответы на эти вопросы зависят от структуры данных, в которой хранится множество элементов. Накладывая незначительные ограничения на структуру исходных данных, можно получить множество разнообразных стратегий поиска различной степени эффективности.
Поиском по заданному аргументу называется алгоритм, определяющий соответствие ключа с заданным аргументом. Результатом работы алгоритма поиска может быть нахождение этого данного или отсутствие его в таблице. В случае отсутствия данного возможны две операции:
Пусть k - массив ключей. Для каждого k(i) существует r(i) - данное. Key - аргумент поиска. Ему соответствует информационная запись rec. В зависимости от того, какова структура данных в таблице, различают несколько видов поиска.
Рассмотрим основные из них
Применяется в том случае, если неизвестна организация данных или данные неупорядочены. Тогда производится последовательный просмотр по всей таблице начиная от младшего адреса в оперативной памяти и кончая самым старшим. последовательный поиск в массиве (переменная search хранит номер найденного элемента).for i:=1 to n if k(i) = key then search = i return endif next i search = 0 return На Паскале программа будет выглядеть следующим образом: for i:=1 to n do if k[i] = key then begin search = i; exit; end; search = 0; exit; Эффективность последовательного поиска в массиве можно определить как количество производимых сравнений М. Мmin = 1, Mmax = n. Если данные расположены равновероятно во всех ячейках массива, то Мср » (n + 1)/2. Если элемент не найден в таблице и необходимо произвести вставку, то последние 2 оператора заменяются на n = n + 1 на Паскале k(n) = key n:=n+1; r(n) = rec k[n]:=key; search = n r[n]:=rec; return search:=n; exit; Если таблица данных задана в виде односвязного списка, то производится последовательный поиск в списке (рис. 5.2).
Варианты алгоритмов:
На псевдокоде: q=nil p=table while (p <> nil) do if k(p) = key then search = p return endif q = p p = nxt(p) endwhile s = getnode k(s) = key r(s) = rec nxt(s) = nil if q = nil then table = s else nxt(q) = s endif search = s return |
На Паскале: q:=nil; p:=table; while (p <> nil) do begin if p^.k = key then begin search = p; exit; end; q := p; p := p^.nxt; end; New(s); s^.k:=key; s^.r:=rec; s.^nxt:= nil; if q = nil then table = s else q.^nxt = s; search:= s; exit |
Достоинством списковой структуры является ускоренный алгоритм удаления или вставки элемента в список, причем время вставки или удаления не зависит от количества элементов, а в массиве каждая вставка или удаление требуют передвижения примерно половины элементов. Об этом говорит сайт https://intellect.icu . Эффективность поиска в списке примерно такая же, как и в массиве.
Эффективность последовательного поиска можно увеличить.
Пусть имеется возможность накапливать запросы за день, а ночью их обрабатывать. Когда запросы собраны, происходит их сортировка.
Поиск нужной записи в неотсортированном списке сводится к просмотру всего списка до того, как запись будет найдена. "Начать с начала и продолжать, пока не будет найден искомый ключ, затем остановиться" -это простейший из алгоритмов поиска. Этот алгоритм не очень эффективен, однако он работает на произвольном списке.
Перед алгоритмом поиска стоит важная задача определения местонахож-дения ключа, поэтому он возвращает индекс записи, содержащей нужный ключ. Если поиск завершился неудачей (ключевое значение не найдено), то алгоритм поиска обычно возвращает значение индекса, превышающее верхнюю границу массива.
Здесь и далее предполагается, что массив А состоит из записей, и его описание и задание произведено вне процедуры (массив является глобальным по отношению к процедуре). Единственное, что требуется знать о типе записей - это то, что в состав записи входит поле key - ключ, по которому и производится поиск. Записи идут в массиве последовательно и между ними нет промежутков. Номера записей идут от 1 до n - полного числа записей. Это позволит нам возвращать 0 в случае, если целевой элемент отсутствует в списке. Для простоты мы предполагаем, что ключевые значения не повторяются.
Процедура SequentialSearch выполняет последовательный поиск элемента z в массиве A[1..n].
SequentialSearch(A, z, n)
(1) for i ←1 to n
(2) do if z = A[i].key
(3) then return i
(4) return 0
Анализ наихудшего случая. У алгоритма последовательного поиска два наихудших случая. В первом случае целевой элемент стоит в списке последним. Во втором его вовсе нет в списке. В обоих случаях алгоритм выполнит n сравнений, где n - число элементов в списке.
Анализ среднего случая. Целевое значение может занимать одно из n возможных положений. Будем предполагать, что все эти положения равновероятны, т. е. вероятность встретить каждое из них равна 
. Следовательно, для нахождения i‑го элемента A[i] требуется i сравнений. В результате для сложности в среднем случае мы получаем равенство
Если целевое значение может не оказаться в списке, то количество возможностей возрастает до n + 1. при отсутствии элемента в списке его поиск требует n сравнений. Если предположить, что все n + 1 возможностей равновероятны, то получим
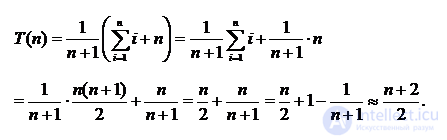
Получается, что возможность отсутствия элемента в списке увеличивает сложность среднего случая на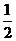 
, но по сравнению с длиной списка, которая может быть очень велика, эта величина пренебрежимо мала.
Рассмотрим общий случай, когда вероятность встретить искомый элемент в списке равна pi , где pi ≥ 0 и 
В этом случае средняя сложность (математическое ожидание) поиска элемента будет равна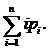 
Хорошим приближением распределения частот к действительности является закон Зипфа: 
для i = 1, 2, ..., n. [n‑е наиболее употребительное в тексте на естественном языке слово встречается с частотой, приблизительно обратно пропорциональной n.] Нормирующая константа выбирается так, что Пусть элементы массива A упорядочены согласно указанным частотам, тогда 
и среднее время успешного поиска составит
что намного меньше 
. Это говорит о том, что даже простой последовательный поиск требует выбора разумной структуры данных множества, который бы повышал эффективность работы алгоритма.
Алгоритм последовательного поиска данных одинаково эффективно выполняется при размещении множества a1, a2,..., an на смежной или связной памяти. Сложность алгоритма линейна - O(n)
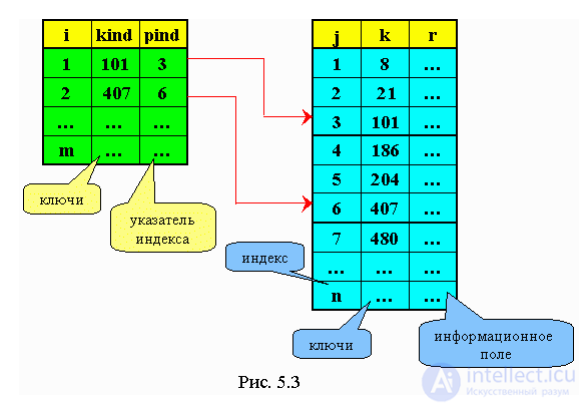
При таком поиске организуется две таблицы: таблица данных со своими ключами (упорядоченная по возрастанию) и таблица индексов, которая тоже состоит из ключей данных, но эти ключи взяты из основной таблицы через определенный интервал (рис. 5.3).
Сначала производится последовательный поиск в таблице индексов по заданному аргументу поиска. Как только мы проходим ключ, который оказался меньше заданного, то этим мы устанавливаем нижнюю границу поиска в основной таблице - low, а затем - верхнюю - hi , на которой ( kind > key ).
Например, key = 101.
Поиск идет не по всей таблице, а от low до hi.
Примеры программ:
Псевдокод: i = 1 while (i <= m) and (kind(i) <= key) do i=i+1 endwhile if i = 1 then low = 1 else low = pind(i-1) endif if i = m+1 then hi = n else hi = pind(i)-1 endif for j=low to hi if key = k(j) then search=j return endif next j search=0 return |
Паскаль: i:=1; while (i <= m) and (kind[i] <= key) do i=i+1; if i = 1 then low:=1 else low:=pind[i-1]; if i = m+1 then hi:=n else hi:=pind[i]-1; for j:=low to hi do if key = k[j] then begin search:=j; exit; end; search:=0; exit; |
Эффективность любого поиска может оцениваться по количеству сравнений C аргумента поиска с ключами таблицы данных. Чем меньше количество сравнений, тем эффективнее алгоритм поиска.
Эффективность последовательного поиска в массиве:
C = 1 ¸ n, C = (n + 1)/2.
Эффективность последовательного поиска в списке - то же самое. Хотя по количеству сравнений поиск в связанном списке имеет ту же эффективность, что и поиск в массиве, организация данных в виде массива и списка имеет свои достоинства и недостатки. Целью поиска является выполнение следующих процедур:
Первая процедура (собственно поиск) занимает для них одно время. Вторая и третья процедуры для списочной структуры более эффективна (т. к. у массивов надо сдвигать элементы).
Если k - число передвижений элементов в массиве, то k = (n + 1)/2.
Ecли считать равновероятным появление всех случаев, то эффективность поиска можно рассчитать следующим образом:
Введем обозначения: m - размер индекса; m = n / p;
p - размер шага
Q = (m+1)/2 + (p+1)/2 = (n/p+1)/2 + (p+1)/2 = n/2p+p/2+1
Продифференцируем Q по p и приравняем производную нулю:
dQ/dp=(d/dp) (n/2p+p/2+1)= - n / 2 p2 + 1/2 = 0
Отсюда
p2=n ;
Подставив ропт в выражение для Q, получим следующее количество сравнений: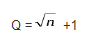 
Порядок эффективности индексно-последовательного поиска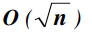 
Логарифмический (бинарный или метод делением пополам) поиск данных применим к сортированному множеству элементов a1 < a2 < ... < an, размещение которого выполнено на смежной памяти. Суть данного метода заключается в следующем: поиск начинается со среднего элемента. При сравнении целевого значения со средним элементом отсортированного списка возможен один из трех результатов: значения равны, целевое значение меньше элемента списка, либо целевое значение больше элемента списка. В первом, и наилучшем, случае поиск завершен. В остальных двух случаях мы можем отбросить половину списка. Действительно, когда целевое значение меньше среднего элемента, мы знаем, что если оно имеется в списке, то находится перед этим средним элементом. Если целевое значение больше среднего элемента, мы знаем, что если оно имеется в списке, то находится после этого среднего элемента. Этого достаточно, чтобы мы могли одним сравнением отбросить половину списка.
Итак, результат сравнения позволяет определить, в какой половине списка продолжить поиск, применяя к ней ту же процедуру.
Процедура BinarySearch выполняет бинарный поиск элемента z в отсортированном массиве A[1..n].
BinarySearch(A, z, n) (1) p←1 (2) r←n (3) while p ≤ r do (4) q← [(p+r)/2] (5) if A[q].key = z (6) then return q (7) else if A[q].key < z (8) then p←q+1 (9) else r←q-1 (10) return 0
Анализ наихудшего случая. Поскольку алгоритм всякий раз делит список пополам, будем предполагать при анализе, что n = 2k ‑ 1 для некоторого k. Ясно, что на некотором проходе цикл имеет дело со списком из 2j ‑ 1 элементов. Последняя итерация цикла производится, когда размер оставшейся части становится равным 1, а это происходит при j = 1 (так как 21 ‑ 1 = 1). Это означает, что при n = 2k ‑ 1 число проходов не превышает k. Следовательно, в наихудшем случае число проходов равно k = log2(n+1).
Анализ среднего случая. Рассмотрим два случая. В первом случае целевое значение наверняка содержится в списке, а во втором его может там и не быть. В первом случае у целевого значения n возможных положений. Будем считать, что все они равновероятны. Представим данные a1 < a2 < ... < an в виде бинарного дерева сравнений, которое отвечает бинарному поиску. Бинарное дерево называется деревом сравнений, если для любой его вершины выполняется условие:
{Вершины левого поддерева} < {Вершина корня} < {Вершины правого поддерева}
Если рассматривать бинарное дерево сравнений, то для элементов в узлах уровня i требуется i сравнений. Так как на уровне i имеется 2i‑1 узел, и при n = 2k ‑ 1 в дереве k уровней, то полное число сравнений для всех возможных случаев можно подсчитать, просумми-ровав произведение числа узлов на каждом уровне на число сравнений на этом уровне.
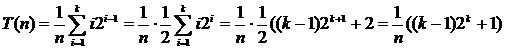
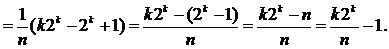
Подставляя 2k = n + 1, получим
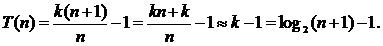
Во втором случае число возможных положений элемента в списке по-прежнему равно n, однако на этот раз есть еще n + 1 возможностей для целевого значения не из списка. Число возможностей равно n + 1, поскольку целевое значение может быть меньше первого элемента в списке, больше первого, но меньше второго, больше второго, но меньше третьего, и так далее, вплоть до возможности того, что целевое значение больше n‑го элемента. В каждом из этих случаев отсутствие элемента в списке обнаруживается после k сравнений. Всего в вычислении участвует 2n + 1 возможностей.
.
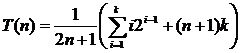Аналогично получаем, что
Значит, сложность поиска является логарифмической O(log2n).
Рассмотренный метод бинарного поиска предназначен главным образом для сортированных элементов a1 < a2 < ... < an на смежной памяти фиксированного размера. Если же размерность вектора динамически меняется, то экономия от использования бинарного поиска не покроет затрат на поддержание упорядо-ченного расположения a1 < a2 < ... < an.
Базовые алгоритмы и методы поиска
поиск подстроки в строке основанный на сравнении с конца
поиск подстроки в строке проводящий сравнение в необычном порядке
На этом все! Теперь вы знаете все про поиск данных, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое поиск данных, последовательный поиск, индексно-последовательный поиск, алгоритмы поиска, логарифмический поиск, бинарный поиск, метод делением пополам, сравнение алгоритмов поиска и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Структуры данных
Термины: Структуры данных