Способы хранения множеств в структуре данных и памяти

Привет, Вы узнаете о том , что такое способы хранения множеств, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое способы хранения множеств, булеан, представление множеств в памяти , настоятельно рекомендую прочитать все из категории Структуры данных.

Основные понятия

Создатель теории множеств Г.Кантор определил понятие множества и элемента множества следующим образом : ”Под множеством мы понимаем собрание определенных отличных друг от друга объектов (реальных или воображаемых), называемых элементами множества, в их общности”. Обычно множества обозначают прописными буквами латинского алфавита, а их элементы – строчными буквами или числами.

Количество элементов в множестве А называется мощностью множества А и обозначается |А| . Если каждому элементу множества А можно поставить в соответствие единственный элемент множества В и каждому элементу множества В можно поставить в соответствие единственный элемент множества А , то множества А и В называются равномощными и обозначается |А|=|В| .

Множество, состоящее из конечного числа элементов, называется конечным .

Множество, не являющиеся конечным, называется бесконечным . Бесконечное множество называется счетным , если оно равномощно множеству N всех натуральных чисел. Говорят, что все элементы счетного множества можно пронумеровать. В противном случае бесконечное множество называется несчетным .

Множество, не содержащее элементов, называется пустым и обозначается 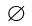или {}.

Обычно в конкретных рассуждениях элементы всех множеств берутся из некоторого одного, достаточно широкого множества U (своего для каждого случая), которое называется универсумом.

Два множества А и В называются равными, если они состоят из одних и тех же элементов (А=В).

Если М - множество, а а – его элемент, то а принадлежит М (а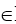 М). Если же а не есть элемент множества М, то а не принадлежит М (а 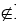М).

Операции над множествами

1. Включение А в В 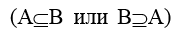истинно, если каждый элемент множества А принадлежит множеству В. В этом случае А называется подмножеством В, а В – надмножеством А.

Множества А и В равны (А=В), если 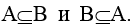. Пустое множество является подмножеством любого множества.

Универсум является надмножеством любого множества.

Множество всех подмножеств множества M называется булеан ом и обозначается :

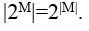
Для конечного множества 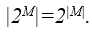. Каждому подмножеству А можно сопоставить |M|-разрядный двоичный вектор С в котором:

C_i=1, есл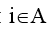и и

C_i=0, если 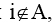, где i – элемент множества M,

С_i – i-й разряд вектора С.

Количество различных |M|-разрядных двоичных векторов равно 2^|M|, следовательно |2^М|=2^|M|.

2. Строгое включение А в В 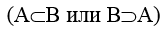истинно, если 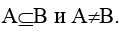. Если , то А есть собственное подмножество В.

3. Объединение А и В (А U В) есть множество, состоящее из всех тех и только тех элементов, которые принадлежат А или В, т.е.

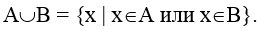
4. Пересечение А и В (А n В) есть множество, состоящее из всех тех и только тех элементов, которые принадлежат каждому из множеств А и В, т.е.

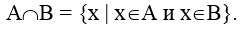
5. Разность А и В (А-В) есть множество, состоящее из всех тех и только тех элементов множества А, которые не принадлежат множеству В, т.е.

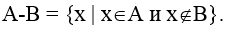
Для обозначения разности множеств в дискретной математике обычно используют символ “\”.

6. Симметрическая разность А и В (АΔВ) есть множество, состоящее из всех тех и только тех элементов множества А, которые не принадлежат множеству В и только тех элементов множества В, которые не принадлежат множеству А, т.е.

7. Дополнение А до универсума U () есть множество, состоящее из всех тех и только тех элементов универсума U, которые не принадлежат множеству А, т.е.

Для любых двух множеств А и В имеет место хотя бы один из следующих пяти случаев (возможностей):

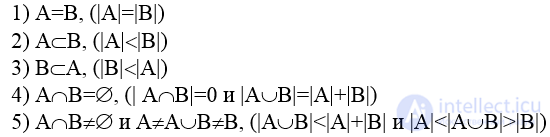
1) А равно В;

2) А строго включено в В;

3) В строго включено в А;

4) А и В не пересекаются;

5) А и В в общем положении.

Если оба множества А и В не пусты, то имеет место только один случай.

На рис.1.1 приведены диаграммы Эйлера (Эйлер (1707-1783) предложил изображать множества в виде кругов еще до создания теории множеств Кантором (1845-1918)), иллюстрирующие операции над множествами. Множества изображаются фигурами (овалами), а результат выделяется графически.

Рис.1.1. Об этом говорит сайт https://intellect.icu . Операции над множествами

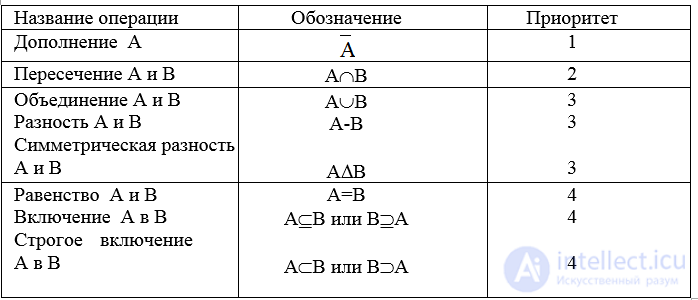
Множество всех подмножеств множества U (булеан) с операциями над множествами образуют алгебру подмножеств (алгебру Кантора) множества U. Выражение, составленное из подмножеств множества U и операций над множествами называется выражением в алгебре подмножеств. Выражение в алгебре подмножеств может содержать скобки, определяющие порядок выполнения операций. Если скобки не указаны, то порядок выполнения операций определяется их приоритетами (табл.1.1). Значением выражения в алгебре подмножеств является подмножество множества U.

Таблица 1.1 Приоритеты операций над множествами

Свойства операций над множествами

1. Идемпотентность:

2. Коммутативность:

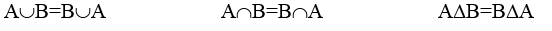
3. Ассоциативность:

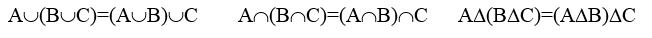
4. Дистрибутивность для пересечения и объединения:

5. Дистрибутивность для пересечения и разности:

6. Дистрибутивность для пересечения и симметрической разности:

7. Дистрибутивность для разности:

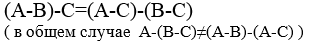
8. Поглощения:

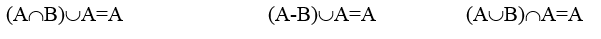
9. Свойства нуля:

10. Свойства единицы:

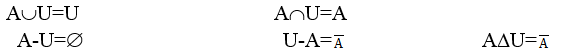
11. Инвалютивность: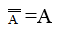

12. Законы де Моргана:

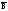
13. Законы де Моргана для разности, пересечения и объединения:

14. Свойства дополнения:

15. Определение разности:

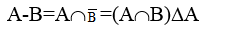
16. Определение объединения:

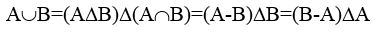
17. Определение пересечения:

Способы задания множеств

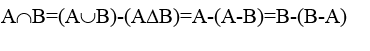
1. Перечислением всех элементов.

A={a,b,c} , B={b,a,c} , C={a} , D={1,2,3,5,9}. Из определения равенства множеств вытекает, что A=B.

2. Заданием характеристического свойства, выделяющего элементы данного множества среди элементов указанного или указанных других множеств.

A={x | x 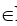N и x<10} (N – множество натуральных чисел),

B={1,2,3,4,5,6,7,8,9} , A=B.

3. Описанием порождающей процедуры с указанием множества (или множеств), которое “пробегает” параметр (или параметры) процедуры.

A={x² | x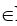 N} – множество всех квадратов натуральных чисел.

Перечислением можно задать только конечное множество, а с помощью характеристического свойства или порождающей процедуры - конечное или бесконечное множество.

Способы представления и хранения множества в памяти компьютера (ЭВМ)

Для представления конечного множества в памяти можно использовать различные способы.

1. Элементы множества А хранятся в переменной А типа массив, мощность множества А – в переменной KA. Количество элементов в массиве А равно мощности универсума. Элементы массива А неупорядочены.

2. Элементы множества А хранятся в переменной А типа массив, мощность множества А – в переменной KA. Количество элементов в массиве А равно мощности универсума. Элементы массива А упорядочены по возрастанию.

3. Элементы универсума нумеруются: U={u₁,…,u_n}. Элементы множества А хранятся в переменной А типа массив, элементы которого типа boolean. Если u_i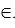 A, то А_i=true, иначе A_i=false. Количество элементов в массиве А равно мощности универсума.

4. Элементы универсума нумеруются: U={u₁,…,u_n}. Множество А представляется кодом С в котором: C_i=1, если u_i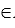 A и C_i=0, если u_i 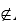A, где С_i – i-й разряд кода С. В зависимости от мощности универсума код С может храниться в простой переменной или в массиве.

5. Для хранения множества можно использовать множественный тип.

Есть четыре основных варианта хранения:

• Массив
• Хэш таблица
• Деревья
• Списки

Массив — это способ хранения, при котором элементы множества расположены последовательно в ячейках.

Самый экономичный вариант, если известна мощность множества, а элементы - данные одного типа.

Список — способ хранения, при котором память выделяется для каждого элемента отдельно и ровно столько, сколько нужно.

Недостаток: необходимо хранить указатель на следующий элемент и тратить время на работу с ним.

Сложность массива и списка - линейна, O(n).

Хеш-таблица — это обобщение способа хранения множества целых чисел (ключей) в форме вектора битов на случай, когда мощность универсума U очень велика по отношению к мощности множеств, с которыми нужно работать.

Хэш-функция — преобразует значения ключей к интервалу [0, m – 1], где m — размер хеш-таблицы, 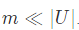Очевидно, что при этом каждому индексу хеш-таблицы будет соответствовать много различных значений ключей. Поэтому, во-первых, в хеш-таблице приходится хранить не биты, а сами значения ключей, а во-вторых, имеется возможность размещать в ней более одного ключа для каждого значения функции отображения (разрешать коллизии).

Если таблица построена правильно и не переполнена, то все функции (удаления, встатвки и тд) выполняются за постоянное время. В худшем случае (если коллизия - повторяющиеся элементы) - сложность линейная O(n).

Дерево двоичного поиска (ДДП) — это способ хранения множества в форме расширяемого упорядоченного списка с сохранением упорядоченности при вставке новых элементов без перемещения уже имеющихся.

ДДП — это дерево с нагруженными узлами, вес в любом узле которого больше любого веса в левом его поддереве и не больше любого веса в правом поддереве. Количество шагов алгоритма поиска элемента множества в таком дереве не превышает его высоты, т. е. имеет сложность O(log n) . Такую же сложность имеют операции вставки нового элемента в дерево и удаления элемента.

ДДП можно получить из упорядоченной последовательности ключей, если двоичное дерево соответствующей мощности разметить внутренним (симметричным) способом, а затем заменить номера узлов соответствующими элементами последовательности. Если последовательность хранится в массиве, то построить ДДП можно методом деления пополам: поместить в корень дерева средний по порядку элемент, затем рекурсивно создать левое поддерево из первой половины последовательности, а правое — из второй.

Недостаток ДДП — в том, что оно хорошо работает только в том случае, если сбалансировано, т. е. длины путей из корня в любой лист примерно одинаковы. Однако при поэлементной вставке в дерево упорядоченной последовательности дерево вырождается, превращаясь в линейный список. Поиск, вставка и удаление в таком дереве будут выполняться не за логарифмическое, а за линейное время. Вероятность вырождения весьма велика. Так, из 7 узлов можно образовать только одно полностью сбалансированное дерево, а полностью вырожденных — 64. Поэтому алгоритмы работы с ДДП часто дополняют автобалансировкой после вставки и удаления. Наиболее употребительны следующие схемы - АВЛ-дерево, RB-дерево, 2-3-дерево.

Программное задание множеств

1. Элементы множества А хранятся в переменной А типа массив, мощность множества А – в переменной KA. Количество элементов в массиве А равно мощности универсума. Элементы массива А неупорядочены.

Алгоритм 1.1 (рис.1.3) вычисления включения А в В (А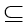 В).

Вход: А-массив, хранящий элементы множества А, КА=|A|;

B-массив, хранящий элементы множества B, КB=|B|;

Выход: F=true, если А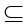 В, иначе F=false.

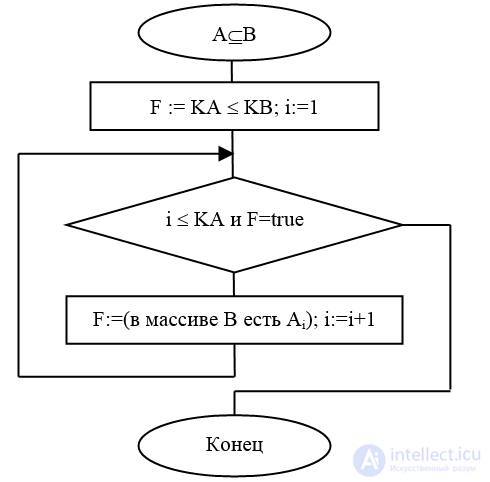
Рис.1.3. Блок-схема алгоритма вычисления включения А в В

Алгоритм 1.2 (рис.1.4) вычисления равенства А и В (А=В).

Вход: А-массив, хранящий элементы множества А, КА=|A|;

B-массив, хранящий элементы множества B, КB=|B|;

Выход: F=true, если А=В, иначе F=false.

Рис.1.4. Блок-схема алгоритма вычисления равенства А и В

Алгоритм 1.3 (рис.1.5) вычисления объединения А и В (А 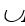В).

Вход: А-массив, хранящий элементы множества А, КА=|A|;

B-массив, хранящий элементы множества B, КB=|B|;

Выход: С-массив, хранящий объединение множеств А и B, КС=|С|;

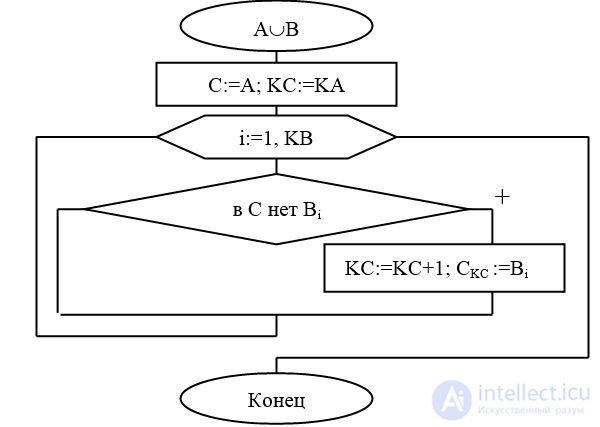
Рис.1.5. Блок-схема алгоритма вычисления объединения А и В

Алгоритм 1.4 (рис.1.6) вычисления пересечения А и В (А 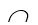В).

Вход: А-массив, хранящий элементы множества А, КА=|A|;

B-массив, хранящий элементы множества B, КB=|B|;

пусть КА 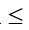KB;

Выход: С-массив, хранящий пересечение множеств А и B, КС=|С|;

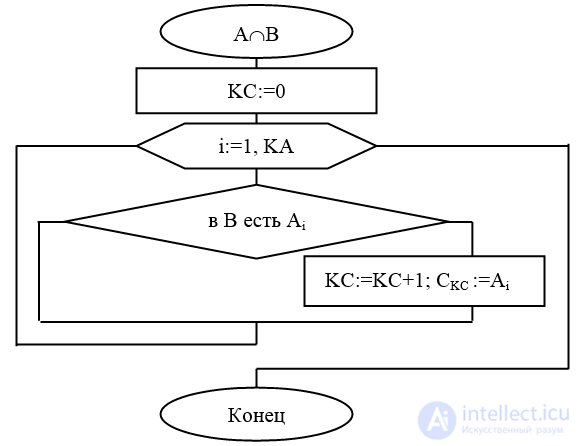
Рис.1.6. Блок-схема алгоритма вычисления пересечения А и В

Алгоритм 1.5 (рис.1.7) вычисления разности А и В (А-В).

Вход: А-массив, хранящий элементы множества А, КА=|A|;

B-массив, хранящий элементы множества B, КB=|B|;

Выход: С-массив, хранящий разность множеств А и B, КС=|С|;

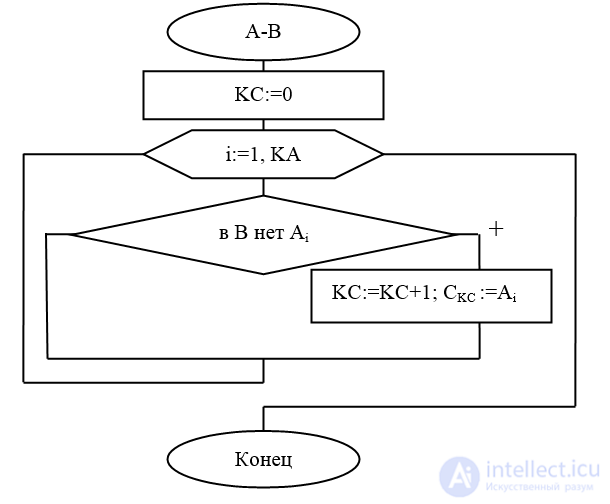
Рис.1.7. Блок-схема алгоритма вычисления разности А и В

Алгоритм 1.6 вычисления симметрической разности А и В (АΔ В).

Вход: А-массив, хранящий элементы множества А, КА=|A|;

B-массив, хранящий элементы множества B, КB=|B|;

Выход: С-массив, хранящий симметрическую разность

множеств А и B, КС=|С|;

1. C:=A-B 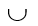B-A; {или C:=(A 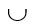B)-(A B) }

2. Конец.

Алгоритм 1.7 (рис.1.8) вычисления дополнения А ().

Вход: А-массив, хранящий элементы множества А, КА=|A|;

Выход: С-массив, хранящий дополнение множества А, КС=|С|;

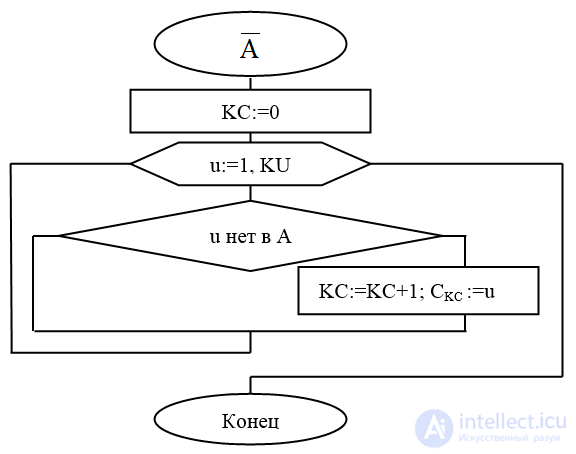
Рис.1.8. Блок-схема алгоритма вычисления дополнения А

Вау!! 😲 Ты еще не читал? Это зря!

• вектор как структура данных , представление вектора в памяти , хранение вектора в памяти ,
• представление разреженного массива в виде массива указателей ,
• разреженные массивы , методы хранения разреженных данных , разреженная матрица , полная матрица ,
• представление графов в памяти компьютера , описание бержа графа , список дуг графа , массив дуг графа ,
• Множество
• Массив
• Хеш таблица
• Деревья
• Списки

Исследование, описанное в статье про способы хранения множеств, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое способы хранения множеств, булеан, представление множеств в памяти и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Структуры данных