Задача о максимальном потоке

Привет, сегодня поговорим про задача о максимальном потоке, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое задача о максимальном потоке , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

Так же, как дорожную карту можно смоделировать ориентированным графом, чтобы найти кратчайший путь из одной точки в другую, ориентированный граф можно интерпретировать как некоторуютранспортную сеть и использовать его для решения задач о потоках вещества в системе трубопроводов.

Каждое ориентированное ребро сети можно рассматривать как канал, по которому движется продукт. Каждый канал имеет заданную пропускную способность, которая характеризует максимальную скорость перемещения продукта по каналу, например, 200 литров жидкости в минуту для трубопровода или 20 ампер для провода электрической цепи. Вершины являются точками пересечения каналов; через вершины, отличные от источника и стока, продукт проходит, не накапливаясь. Об этом говорит сайт https://intellect.icu . Иными словами, скорость поступления продукта в вершину должна быть равна скорости его удаления из вершины.

В задаче о максимальном потоке мы хотим найти максимальную скорость пересылки продукта от источника к стоку, при которой не будут нарушаться ограничения пропускной способности. Основные методы, используемые в алгоритмах решения задач о максимальном потоке, можно применять для решения других задач, связанных с транспортными сетями.

Пусть дан неориентированный граф G = (V, Е).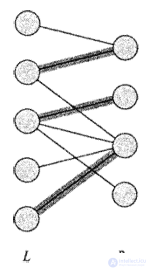 
Паросочетанием (matching) называется подмножество ребер М є Е, такое что для всех вершин v є V в М содержится не более одного ребра, инцидентного v.

Ограничимся рассмотрением задачи поиска максимальных паросочетаний в двудольных графах. Мы предполагаем, что множество вершин можно разбить на два подмножества V = L U R, где L и R не пересекаются, и все ребра из Е проходят между L и R. Далее мы предполагаем, что каждая вершина из V имеет по крайней мере одно инцидентное ребро.

Задача поиска максимального паросочетания в двудольном графе имеет множество практических приложений. В качестве примера можно рассмотреть паросочетание множества машин L и множества задач R, которые должны выполняться одновременно. Наличие в Е ребра (u,v) означает, что машина u є L может выполнять задачу v є R. Максимальное паросочетание обеспечивает максимальную загрузку машин.

В данном разделе описывается классический метод Форда-Фалкерсона (Ford and Fulkerson) для поиска максимального потока. В качестве приложения данного метода осуществляется поиск максимального паросочетания в неориентированном двудольном графе.

На этом все! Теперь вы знаете все про задача о максимальном потоке, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое задача о максимальном потоке и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов