Метро(решение через графы)

Привет, сегодня поговорим про метро решение через графы , обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое метро решение через графы , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

Белорусская республиканская олимпиада, 2002.

Задание

В некотором городе есть метро, состоящее из N (1 <= N <= 1000) станций и M (0 <= M <= 500 000) линий, соединяющих их. Каждая линия обеспечивает проезд между какими-то двумя станциями в обе стороны. Между любой парой станций проведено не более одной линии. Сеть метро построена таким образом, чтобы с каждой станции можно было проехать на каждую (возможно, через промежуточные станции). Назовем это свойство связностью метро.

В связи с изобретением принципиально нового вида транспорта метро стало убыточным, и его работу решили прекратить. На заседании мэрии города было постановлено закрывать каждый год по одной станции, но так, чтобы связность метро каждый раз сохранялась. При закрытии какой-либо станции линии, ведущие от этой станции к другим, естественно, тоже перестают функционировать.

По введенной информации о сети метро разработать какой-либо порядок закры- тия станций, при котором метро всегда будет оставаться связным. Например, пусть метро выглядит так, как показано на рисунке.

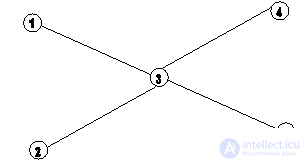
Тогда станции можно закрывать, например, в порядке 1,2,4,3,5. Об этом говорит сайт https://intellect.icu . А порядок 3,1,2,4,5 — не подходит, так как после закрытия 3-й станции метро распадется на четыре не связных части.

Ввод

Первая строка входного файла будет содержать числа N и M. В следующих М строках находится информация о линиях. Каждая из этих строк содержит через пробел числа Ai и Bi (Ai, Bi) — две станции, которые соединяет i-я линия.

Вывод

Выходной файл должен состоять из N строк. Каждая строка должна содержать одно число — номер станции. Вывести станции нужно в порядке их закрытия.

Пример ввода       Пример вывода
5 4                1
3 1                2  
3 2                4
3 4                3
3 5                5

Решение     

Естественно представить станции метро вершинами графа, а линии, их соединяющие, — ребрами графа. По условиям задачи длины линий не имеют значения, поэтому мы можем задать значения весов всех ребер равными 1.

Теперь нам достаточно найти остовное дерево (искать остовое дерево будем по алгоритму Прима), а затем обойти исходный граф поиском в глубину, используя только ребра, включенные в остовное дерево.

Формальное описание     

Metro()
1. Считать из файла список ребер графа, создать матрицу смежности графа.
2. Использовать алгоритм Прима для нахождения наименьшего остового дерева 
   (выполнять пп 2.1-2.4):
   3.1. Добавить все вершины в очередь, инициализировать значение ключа
        бесконечностью, а массив с предыдущими вершинами -1.
   3.2. Присвоить стартовой вершине значение ключа 0.
   3.3. Пока в очереди присутствуют вершины, повторять пп. 3.3.1-3.3 :
        3.3.1. Найти вершину с минимальным ключом.
        3.3.2. Удалить найденную вершину из очереди.
        3.3.3. Обновить ключ для всех инцидентных вершин, которые 
               находятся в очереди.
        3.3.4. Для все инцидентных вершин, которые находятся в очереди,
               предыдущей к ним вершиной считать текущую вершину.
3. Построить матрицу смежности для поученного остового дерева.
4. Обойти все вершины остового дерева вглубь, выводя вершины на экран.

Пример схемы метро.

Порядок закрытия станций: 3, 8, 9, 7, 6, 5, 4, 2, 1.

На этом все! Теперь вы знаете все про метро решение через графы , Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое метро решение через графы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов