Лекция
Привет, Вы узнаете о том , что такое классы сложности алгоритмов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое классы сложности алгоритмов, класс сложности, класс ph, класс bqp, класс p, класс np класс bpp , класс l, класс nl, класс zpp , класс rp, класс nc , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
В теории алгоритмов классами сложности называются множества вычислительных задач, примерно одинаковых по сложности вычисления. Говоря более узко, классы сложности — это множества предикатов (функций, получающих на вход слово и возвращающих ответ 0 или 1), использующих для вычисления примерно одинаковые количества ресурсов.
Для каждого класса существует категория задач, которые являются «самыми сложными». Это означает, что любая задача из класса сводится к такой задаче, и притом сама задача лежит в классе. Такие задачи называют полными задачами для данного класса. Наиболее известными являются NP-полные задачи.
Полные задачи — хороший инструмент для доказательства равенства классов. Достаточно для одной такой задачи предоставить алгоритм, решающий ее и принадлежащий более маленькому классу, и равенство будет доказано.
Каждый класс сложности (в узком смысле) определяется как множество предикатов, обладающих некоторыми свойствами. Типичное определение класса сложности выглядит так:
Классом сложности X называется множество предикатов P(x), вычислимых на машинах Тьюринга и использующих для вычисления O(f(n)) ресурса, где n — длина слова x.
В качестве ресурсов обычно берутся время вычисления (количество рабочих тактов машины Тьюринга) или рабочая зона (количество использованных ячеек на ленте во время работы). Языки, распознаваемые предикатами из некоторого класса (то есть множества слов, на которых предикат возвращает 1), также называются принадлежащими тому же классу.
Кроме того, многие классы могут также быть описаны в терминах математической логики или теории игр.
Классы принято обозначать прописными буквами. Дополнение к классу C (то есть класс языков, дополнения которых принадлежат C) обозначается co-C.
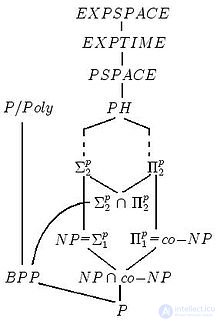
Иерархия классов сложности

Различные классы сложности сортируют задачи в иерархическом виде. Один класс может содержать все задачи другого, плюс задачи, требующие дополнительных вычислительных ресурсов.
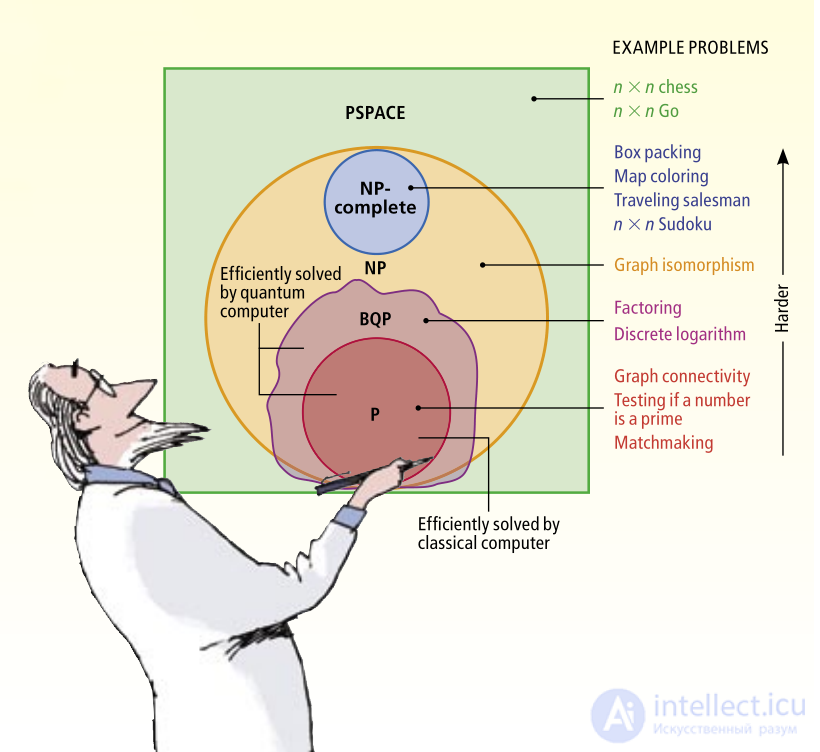
Все классы сложности находятся в иерархическом отношении: одни включают в себя другие. Однако про большинство включений неизвестно, являются ли они строгими. Одна из наиболее известных открытых проблем в этой области — равенство классов P и NP. Если это предположение верно (в чем многие ученые сомневаются), то представленная справа иерархия классов сильно свернется. На данный момент наиболее распространенной является гипотеза о невырожденности иерархии (то есть все классы различны). Кроме того, точно известно, что EXPSPACE не равен классу PSPACE.
Рассмотрим функцию f и входную цепочку длиной n. Тогда класс DTIME(f(n)) определяют как класс языков, принимаемых детерминированными машинами Тьюринга, заканчивающими свою работу за время, не превосходящее f(n). Класс NTIME(f(n)), в свою очередь, определяют как класс языков, принимаемых недетерминированной машиной Тьюринга, заканчивающими свою работу за время, не превосходящее f(n). Отметим, что ограничения на память при определении данных классов отсутствуют.
Аналогично иерархии по времени вводится иерархия по памяти. Класс DSPACE(f(n)) обозначает класс языков, принимаемых детерминированными машинами Тьюринга, использующих не более f(n) ячеек памяти на рабочих лентах. Класс NSPACE(f(n)) определяют как класс языков, принимаемых недетерминированными машинами Тьюринга, использующих не более f(n) ячеек памяти на рабочих лентах. Временные ограничения при определении данных классов отсутствуют.
Аналогично определяются и другие подобные рассмотренным выше классы. Приведем использующиеся сокращения:
Какова фундаментальная сложность задачи? Такова постановка базовой задачи специалистов по информатике, пытающихся рассортировать задачи по т.н. классам сложности. Это группы, содержащие все вычислительные задачи, требующие не более фиксированного количества вычислительных ресурсов – таких, как время или память. Возьмем простой пример с большим числом типа 123 456 789 001. Можно задать вопрос: является ли оно простым числом – таким, которое делится только на 1 и себя? Специалисты по информатике могут ответить на него при помощи быстрых алгоритмов – таких, что не начинают тормозить на произвольно больших числах. В нашем случае окажется, что это число не является простым. Затем мы можем задать вопрос: каковы его простые множители? А вот для ответа на него быстрого алгоритма не существует – только если использовать квантовый компьютер. Поэтому специалисты по информатике считают, что две этих задачи относятся к разным классам сложности.
Существует множество различных классов сложности, хотя в большинстве случаев исследователи не смогли доказать, что один класс четко отличается от других. Доказательства различия между классами – одни из самых трудных и важных задач в этой области.
Разница между классами может быть едва различимой или явной, и хорошо разбираться во всех классах довольно трудно. Поэтому мы собрали этот справочник по семи наиболее фундаментальным классам сложности. И да не будете вы больше путать между собой BPP и BQP.
Обозначает: полиномиальное время
Краткое описание: все задачи, которые легко может решить классический (не квантовый) компьютер.
Точное описание: алгоритмы класса P должны прекратить работу и выдать правильный ответ не более чем за время nc, где n – длина входных данных, c – константа.
Типичные задачи:
Что исследователи хотели бы знать: совпадает ли P с NP? Совпадение совершило бы революцию в информатике и лишило бы смысла большую часть криптографических систем (но в это почти никто не верит).
Обозначает: недетерминированное полиномиальное время
Краткое описание: все задачи, которые классический компьютер может легко проверить при наличии решения.
Точное описание: проблема попадает в класс NP, когда при наличии ответа «да» существует краткое доказательство корректности ответа. Если входные данные представляют собой строку X, а вам надо решить, совпадает ли ответ с «да», тогда кратким доказательством будет другая строка, Y, которую можно использовать для проверки корректности ответа «да» за полиномиальное время. (Y иногда называют «кратким свидетелем» – у всех задач из NP есть краткие свидетели, благодаря которым их можно проверить).
Типичные задачи:
Что исследователи хотели бы знать: P = NP? Специалисты по информатике и близко не подошли к решению этой задачи.
Обозначает: полиномиальная иерархия
Краткое описание: PH – это обобщение NP. Она содержит все задачи, которые можно получить, начав с задачи из NP, и накладывая дополнительные уровни сложности.
Точное описание: PH содержит задачи с некоторым количеством различных «кванторов», усложняющих эти задачи. Пример задачи с различными кванторами: Если нам дано X, существует ли такой Y, что для каждого Z существует W, при котором выполняется R? Чем больше в задаче кванторов, тем она сложнее, и тем выше полиномиальная иерархия.
Типичная задача: определить, действительно ли существует клика размера 50, и не существует клики размером 51.
Что исследователи хотели бы знать: никто пока не смог доказать, что PH отличается от P. Эта задача эквивалентна равенству P и NP, поскольку, если вдруг окажется, что P = NP, тогда все PH низведутся до P (P = PH).
Обозначает: полиномиальное ограничение пространства
Краткое описание: PSPACE содержит все задачи, которые можно решить, используя разумное количество памяти.
Точное описание: При решении задач PSPACE вы уже не переживаете за время, вы переживаете только за количество памяти, которое требуется для работы алгоритма. Специалисты по информатике доказали, что PSPACE содержит PH, которая содержит NP, которая содержит P.
Типичная задача: все задачи из P, NP и PH содержатся в PSPACE.
Что исследователи хотели бы знать: отличается ли PSPACE от P?
Обозначает: квантово-полиномиальное время с ограничением вероятности ошибок
Краткое описание: все задачи, которые легко можно решить на квантовом компьютере.
Точное описание: все задачи, которые можно решить на квантовом компьютере за полиномиальное время.
Типичная задача: найти простые множители целого числа.
Что исследователи хотели бы знать: Пока что доказано, что BQP содержится в PSPACE, и что BQP содержит P. Исследователи не знают, содержится ли BQP в NP, но они считают, что два этих класса сравнивать нельзя – есть задачи, входящие в NP, но не входящие в BQP, и наоборот.
Обозначает: экспоненциальное время
Краткое описание: все задачи, которые можно решить за экспоненциальное время на классическом компьютере.
Точное описание: EXP содержит все предыдущие классы — P, NP, PH, PSPACE и BQP. Исследователи доказали, что он отличается от P – они обнаружили задачи, входящие в EXP, и не входящие в P.
Типичная задача: обобщения игр типа шахмат и шашек. Если шахматная доска может быть любого размера, то задача определения наличия преимущества у одного из игроков становится задачей из EXP.
Что исследователи хотели бы знать: они хотели бы доказать, что PSPACE не содержит EXP. Они считают, что существуют задачи, входящие в EXP, но не входящие в PSPACE, потому что иногда для решения задачи из EXP требуется очень много времени. Исследователи знают, как разделять EXP и P.
Обозначает: полиномиальное время с ограничением вероятности ошибок
Краткое описание: задачи, которые можно быстро решить при помощи алгоритмов, использующих случайность.
Точное описание: BPP совпадает с P, с той разницей, что алгоритм может включать шаги, в которых принятие решений происходит случайно. Алгоритмам в BPP необходимо давать правильные ответы с вероятностью, близкой к 1.
Типичная задача: у вас есть две различные формулы, выдающие многочлены со множеством переменных. Вычисляют ли эти формулы один и тот же многочлен? Это задача проверки полиномиальной идентичности.
Что исследователи хотели бы знать: Равны ли BPP и P. Если они равны, тогда любой алгоритм со случайностями можно было бы избавить от случайностей. Они считают, что так и есть – что для каждой задачи, для которой существует эффективный случайный алгоритм, существует и эффективный детерминистский алгоритм – но пока не смогли этого доказать.
Это статья о классах языков для детерминированной машины Тьюринга.
Класс языков L — множество языков, разрешимых на детерминированной машине Тьюринга с использованием дополнительной памяти для входа длиной n.
Класс языков NL — множество языков, разрешимых на недетерминированной машине Тьюринга с использованием дополнительной памяти для входа длиной n.
Примеры:
Преобразователь, требующий логарифмической памяти — машина Тьюринга с тремя лентами: входной, доступной только на чтение, выходной, доступной только на запись и рабочей лентой, на которой может использоваться не более O(log(n)) ячеек.
Функция, вычисляемая таким преобразователем называется функцией, вычисляемой с логарифмической памятью.
Задача A логарифмически по памяти сводится к задаче B, если есть логарифмическая по памяти функция, при помощи которой задача А сводится к задаче В. Обозначается
Язык называется NL-полным если он принадлежит NL и любой язык из NL сводится к нему логарифмически по памяти.
Теорема:
Следствие:
Если NL-полный язык принадлежит L, то L = NL
Утверждение:
PATH — NL-полная задача.
Следствие:
.
Класс coNL — языки, дополнения до которых лежат в NL.
Теорема Иммермана:
NL = coNL
Алгоритм отождествляется с детерминированной машиной Тьюринга, которая вычисляет ответ по данному на входную ленту слову из входного алфавита . Временем работы алгоритма
при фиксированном входном слове x называется количество рабочих тактов машины Тьюринга от начала до остановки машины. Сложностью функции
, вычисляемой некоторой машиной Тьюринга, называется функция
, зависящая от длины входного слова и равная максимуму времени работы машины по всем входным словам фиксированной длины:
.
Если для функции f существует машина Тьюринга M такая, что для некоторого числа c и достаточно больших n, то говорят, что она принадлежит классу P, или полиномиальна по времени.
Согласно тезису Черча — Тьюринга, любой мыслимый алгоритм можно реализовать на машине Тьюринга. Для любого языка программирования можно определить класс P подобным образом (заменив в определении машину Тьюринга на реализацию языка программирования). Если компилятор языка, на котором реализован алгоритм, замедляет исполнение алгоритма полиномиально (то есть время выполнения алгоритма на машине Тьюринга меньше некоторого многочлена от времени выполнения его на языке программирования), то определения классов P для этого языка и для машины Тьюринга совпадают. Код на ассемблере допускает преобразование в машину Тьюринга с небольшим полиномиальным замедлением, а поскольку все существующие языки допускают компиляцию в ассемблер (опять же, с полиномиальным замедлением), то определения класса P для машин Тьюринга и для любого существующего языка программирования совпадают.
Иногда под классом P имеют в виду более узкий класс функций, а именно класс предикатов (функций ). В таком случае языком L, который распознается данным предикатом, называется множество слов, на которых предикат равен 1. Языками класса P называются языки, для которых существуют распознающие их предикаты класса P. Очевидно, что если языки
и
лежат в классе P, то и их объединение, пересечение и дополнения также лежат в классе P.
Класс P является одним из самых узких классов сложности. Об этом говорит сайт https://intellect.icu . Алгоритмы, принадлежащие ему, принадлежат также классу NP, классу BPP (как допускающие полиномиальную реализацию с нулевой ошибкой), классу PSPACE (т.к. зона работы на машине Тьюринга всегда меньше времени), классу P/Poly (для доказательства этого факта используется понятие протокола работы машины, который переделывается в булеву схему полиномиального размера).
Уже более 30 лет остается нерешенной задача о равенстве классов P и NP. Если они равны, то любую задачу из класса NP можно решить быстро (за полиномиальное время). Однако научное сообщество склоняется в сторону отрицательного ответа на этот вопрос. Кроме того, не доказана и строгость включения в более широкие классы, например, в PSPACE, но равенство P и PSPACE выглядит на данный момент очень сомнительно.
Примерами задач из класса P являются целочисленное сложение, умножение, деление, взятие остатка от деления, умножения матриц, выяснение связности графов, сортировка множества из n чисел, нахождение эйлерова цикла на графе из m ребер, обнаружение в тексте длиной n некоторого слова, построение покрывающего дерева минимальной стоимости, линейное программирование и некоторые другие.
Существует много задач, для которых не найдено полиномиального алгоритма, но не доказано, что его не существует. Соответственно, неизвестно, принадлежат ли такие задачи классу P. Вот некоторые из них:
Поскольку часто приходится вычислять значения функций на входных данных большого объема, нахождение полиномиальных алгоритмов для вычисления функций является очень важной задачей. Считается, что вычислять функции, не лежащие в классе P, заметно сложнее, чем лежащие. Большинство алгоритмов, лежащих в классе P, имеют сложность, не превосходящую многочлен небольшой степени от размера входных данных. Например, стандартный алгоритм перемножения матриц требует n3 умножений (хотя существуют и более быстрые алгоритмы, например, алгоритм Штрассена). Степень многочлена редко бывает большой. Один из таких случаев — предложенный в 2002 году индийскими математиками тест Агравала — Каяла — Саксены, выясняющий, является ли число n простым, за O(log6n) операций.
В теории алгоритмов классом NP (от англ. non-deterministic polynomial) называют множество задач разрешимости, решение которых возможно проверить на машине Тьюринга за время, не превосходящее значения некоторого многочлена от размера входных данных, при наличии некоторых дополнительных сведений (так называемого сертификата решения).
Эквивалентно класс NP включает задачи, которые можно за полиномиальное время решить на недетерминированной машине Тьюринга.
Задачи, имеющие полиномиальные по времени алгоритмы решения, можно решать с помощью компьютера значительно быстрее, чем путем прямого перебора, время которого экспоненциально. Это обуславливает практическое значение проблемы о равенстве классов P и NP.
Класс сложности NP определяется для множества языков, то есть множеств слов над конечным алфавитом . Язык L называется принадлежащим классу NP, если существуют двуместный предикат
из класса P (то есть вычислимый за полиномиальное время) и константа
такие, что для всякого слова x условие «x принадлежит L» равносильно условию «найдется y длины меньше
такой, что верно
» (где |x| — длина слова x). Слово y называется сертификатом принадлежности x языку L. Таким образом, если у нас есть слово, принадлежащее языку, и еще одно слово-свидетель ограниченной длины (которое бывает трудно найти), то мы быстро сможем удостовериться в том, что x действительно принадлежит L.
Эквивалентное определение можно получить, используя понятие недетерминированной машины Тьюринга (то есть такой машины Тьюринга, у программы которой могут существовать разные строки с одинаковой левой частью). Если машина встретила «развилку», то есть неоднозначность в программе, то дальше возможны разные варианты вычисления. Предикат , который представляет данная недетерминированная машина Тьюринга, считается равным единице, если существует хоть один вариант вычисления, возвращающий 1, и нулю, если все варианты возвращают 0. Если длина вычисления, дающего 1, не превосходит некоторого многочлена от длины x, то предикат называется принадлежащим классу NP. Если у языка существует распознающий его предикат из класса NP, то язык называется принадлежащим классу NP. Это определение эквивалентно приведенному выше: в качестве свидетеля можно взять номера нужных веток при развилках в вычислении. Так как для x принадлежащему языку длина всего пути вычисления не превосходит многочлена от длины x, то и длина свидетеля также будет ограничена многочленом от длины x.
Всякую задачу о принадлежности слова x языку L, лежащую в классе NP, можно решить за экспоненциальное время перебором всех возможных сертификатов длины меньше . Для ее решения на квантовом компьютере можно использовать GSA. В этом случае общее количество всех возможных сертификатов, которые нужно перебрать, можно определить по формуле суммы
членов геометрической прогрессии со знаменателем, равным числу символов
в алфавите {\displaystyle \Sigma }
, и 1-м членом, равным 1:
Поэтому для поиска нужного сертификата методом GSA требуется Q-битов. Сертификат будет найден за время, не превышающее
.
Класс языков, дополнения которых принадлежат NP, называется классом co-NP, хотя и не доказано, что этот класс отличен от класса NP. Пересечение классов NP и co-NP содержит класс P. В частности, класс NP включает в себя класс P. Однако ничего не известно о строгости этого включения.
Задача о равенстве классов P и NP является одной из центральных открытых проблем теории алгоритмов. Если они равны, то любую задачу из класса NP можно будет решить быстро (за полиномиальное время). Однако научное сообщество склоняется в сторону отрицательного ответа на этот вопрос.
Класс NP включается в другие, более широкие классы, например, в класс PH. Существуют также открытые вопросы о строгости его включения в другие классы.
Можно привести много задач, про которые на сегодняшний день неизвестно, принадлежат ли они P, но известно, что они принадлежат NP. Среди них:
Среди всех задач класса NP можно выделить «самые сложные» — NP-полные задачи. Если удастся решить любую из них за полиномиальное время, то все задачи класса NP также можно будет решить за полиномиальное время.
Класс сложности PH (от англ. polynomial hierarchy) — объединение всех классов сложности из полиномиальной иерархии:
Таким образом, предикат принадлежит классу PH, если существует такое k, что предикат принадлежит классу . Также говорят, что язык, распознаваемый таким предикатом (то есть множество всех слов, на которых предикат возвращает 1), принадлежит классу PH.
Класс языков PH в точности совпадает с классом языков, выразимых с помощью логики второго порядка.
Назовем конечной игрой следующую структуру. Имеется дерево, вершины которого помечены именами двух игроков A и B (все вершины одного уровня помечены одним и тем же именем, ходы чередуются), а ребра соответствуют ходам игроков. Пусть дано некоторое начальное слово x — начальная конфигурация игры. Тогда количество уровней в дереве (т.е. количество ходов) равно некоторой функции f от длины x, а каждое ребро помечено словом длины g от длины x (ходом игрока является слово, которым помечено ребро). Имеется предикат от начальной конфигурации и последовательности ходов игроков, который определяет, кто выиграл (если он равен 1, то выиграл первый игрок). Поскольку игра конечна, то выигрышная стратегия всегда существует либо у первого игрока, либо у второго. Назовем игру распознающей язык L, если для каждого слова x из L у игрока A есть выигрышная стратегия.
Класс PH является классом всех языков, распознаваемых играми, такими, что f равна константе (т.е. количество ходов в игре фиксировано и не зависит от длины входного слова), а g является многочленом от длины x (таким образом, из каждой вершины дерева, кроме последней, исходит по ребер, где
— этот многочлен).
В отличие от составляющих класс PH классов полиномиальной иерархии, про PH доподлинно известно, что он замкнут относительно пересечения, объединения и дополнения языков. Это означает, что если языки и
принадлежат PH, то языки
,
и
принадлежат PH.
Для доказательства достаточно предъявить игры, распознающие эти комбинации языков, если имеются игры, распознающие и
. Для дополнения передадим право первого хода другому игроку и в качестве предиката выигрыша возьмем
. Для пересечения возьмем две игры, распознающие
и
, такими, что количество ходов в них одинаковое, а вторую начинает не тот игрок, который делает последний ход в первой. После этого в каждую концевую вершину первой игры добавим вторую игру, а в качестве предиката выигрыша возьмем
, где
и
— разбиение всей последовательности ходов на две: часть, соответствующая первой игре, и часть, соответствующая второй. Для объединения возьмем игры, распознающие
и
, с одинаковым количеством ходов и одинаковым первым игроком. Создадим новую вершину, соответствующую другому игроку, и прицепим к ней одно дерево первой игры (над этим ребром напишем слово 00...0) и оставшиеся
ребер второй игры. Первое слово игры обозначим z, а остальную часть последовательности слов —
, а в качестве предиката выигрыша возьмем
.
По определению, в класс PH включены все классы полиномиальной иерархии, в том числе P и NP. Кроме того, он содержит вероятностные классы, такие как класс BPP (т.к. BPP содержится в классе ). Сам класс PH включен в класс PSPACE и класс PPP (класс задач, которые решаются за полиномиальное время на машине Тьюринга с доступом к оракулу класса PP).
Открытые проблемы
Установлено, что P = NP, тогда и только тогда, когда P = PH. Это утверждение может облегчить доказательство того, что P ≠ NP (если это так), поскольку нужно будет лишь отделить P от более общего класса, чем NP.
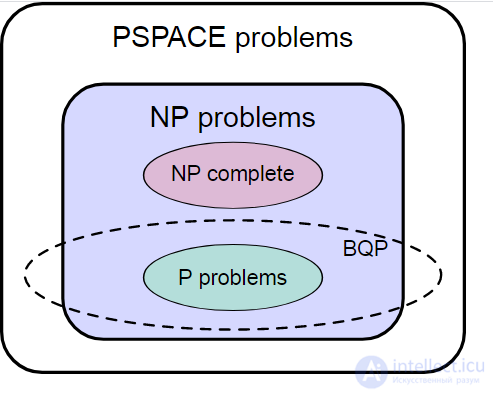
В теории алгоритмов классом сложности BQP (от англ. bounded error quantum polynomial time) называется класс проблем разрешимости, которые могут быть решены квантовым компьютером за полиномиальное время (время работы над задачей полиномиально зависит от размера входных данных), обеспечив при этом вероятность получения верного ответа как минимум 2/3 для любого входа. Является квантовым аналогом класса BPP.
Другими словами, задача относится к классу BQP, если существует квантовый алгоритм (алгоритм для квантового компьютера), решающий данную проблему с высокой вероятностью и работающий гарантированно не более чем за полиномиальное время. Для произвольного запуска алгоритма вероятность получения неверного ответа должна быть не более 1/3.
В теории сложности вычислений классом NC (от англ. Nick’s Class) называют множество задач разрешимости, разрешимых за полилогарифмическое время на параллельном компьютере с полиномиальным числом процессоров. Другими словами, задача принадлежит классу NC, если существуют константы и
такие, что она может быть решена за время
при использовании
параллельных процессоров. Стивен Кук назвал его «Классом Ника» в честь Ника Пиппенжера[en], который провел обширные исследования схем с полилогарифмической глубиной и полиномиальным размером.
Так же, как класс P можно считать классом податливых задач (Тезис Кобхэма[en]), так и NC можно считать классом задач, которые могут быть эффективно решены на параллельном компьютере. NC — это подмножество P, потому что параллельные полилогарифмические вычисления можно симулировать с помощью последовательных полиномиальных вычислений. Неизвестно, верно ли NP = P, но большинство ученых считает, что нет, из чего следует, что скорее всего существуют податливые задачи, которые последовательны «от природы», и не могут быть существенно ускорены при использовании параллелизма. Так же, как класс NP-полных задач можно считать классом «скорее всего неподатливых» задач, так и класс P-полных задач, при сведении к NC, можно считать «скорее всего не параллелизуемым» или «скорее всего последовательным от природы».
Параллельный компьютер в определении можно считать параллельной машиной с произвольным доступом (PRAM — от англ. parallel, random-access machine). Это параллельный компьютер с центральным пулом памяти, любой процессор которого может получить доступ к любому биту за константное время. На определение NC не влияет способ, с помощью которого PRAM осуществляет одновременный доступ нескольких процессоров к одному биту.
NC может быть определен, как множество задач разрешимости, разрешимых распределенной Булевой схемой с полилогарифмической глубиной и полиномиальным числом вентилей.
NC включает в себя много задач, в том числе:
Часто алгоритмы для этих задач придумывались отдельно и не могли быть наивной адаптацией известных алгоритмов — Метод Гаусса и алгоритм Евклида полагаются на то, что операции выполняются последовательно.
NCi — это множество задач разрешимости, разрешимых распределенными булевыми схемами с полиномиальным количеством вентилей (с количеством входов, не большим двух) и глубиной , или разрешимых за время
параллельным компьютером с полиномиальным числом процессоров. Очевидно,
что представляет собой NC-иерархию.
Мы можем связать классы NC с классами памяти L, NL и AC :
Классы NC и AC одинаково определены, за исключением неограниченности количества входов у вентилей для класса AC. Для каждого верно :
Следствием этого является NC = AC. Известно, что оба включения строгие для . Похожим образом можем получить, что NC эквивалентен множеству задач, решаемых на переменной машине Тьюринга с числом выборов на каждом шаге не большим, чем двух, и с O(log n) памяти и
альтерациями.
Один из больших открытых вопросов теории сложности вычислений — является ли собственным каждое вложение NC-иерархии. Как было замечено Пападимитриу, если для какого-т верно NCi = NCi+1, то NCi = NCj для всех
, и как следствие, NCi = NC. Это наблюдение называется сворачиванием NC-иерархии, потому что даже из одного равенстве в цепи вложений:
следует, что вся NC-иерархия «сворачивается» до какого-то уровня {\displaystyle i}. Таким образом, возможны два варианта:
Широко распространено мнение, что верно именно (1), хотя пока не обнаружено никаких доказательств в отношении истинности того или иного утверждения.
Ветвящаяся программа с переменными, шириной
и длиной
состоит из последовательности инструкций длины
. Каждая инструкция — это тройка
, где
— это индекс переменной, которую нужно проверить
, а
и
— это функции перестановки из
в
. Числа
называются состояниями ветвящейся программы. Программа начинается в состоянии 1, и каждая инструкция
изменяет состояние
в
или , в зависимости от того, равна ли
-ая переменная 0 или 1.
Семейство ветвящихся программ состоит из ветвящихся программ с переменными для каждого
.
Легко показать, что любой язык на
может быть распознан семейством ветвящихся программ с шириной 5 и экспоненциальной длиной, или семейством с экспоненциальной шириной и линейной длиной.
Каждый регулярный язык на может быть распознан семейством ветвящихся программ с константной шириной и линейным числом инструкций (так как ДКА может быть преобразован в ветвящуюся программу). BWBP обозначает класс языков, распознаваемых семейством ветвящихся программ с ограниченной шириной и полиномиальной длиной (англ BWBP — bounded width and polynomial length).[10].
Теорема Баррингтона[11] утверждает, что BWBP — это в точности нераспределенный NC1. Доказательство теоремы использует неразрешимость группы симметрии .[10]
Докажем, что ветвящаяся программа (ВП) с константной шириной и полиномиальным размером может быть превращена в схему из NC1.
От противного: пусть есть схема C из NC1. Без ограничения общности, будем считать что в ней используются только вентили И и НЕ.
Определение: ВП называется {\displaystyle \sigma }-вычисляющей булеву функцию
или
, если при {\displaystyle f=0}
она дает результат — тождественную перестановку, а при
ее результат —
-перестановка. Так как наша схема C описывает какую-то булеву функцию {\displaystyle f}
и только ее, можем взаимно заменять эти термины.
Для доказательства будем использовать две леммы:
Лемма 1: Если есть ВП, -вычисляющая
, то существует и ВП,
-вычисляющая
(то есть, равная
при
, и равная
при
.
Доказательство: так как и
— циклы, а любые два цикла являются сопряженными, то существует такая перестановка
, что
=
. Тогда домножим на
перестановки
и
из первой инструкции ВП слева (чтобы получить перестановки
и
), а перестановки из последней инструкции домножим на
справа (получим
и
). Если до наших действий (без ограничения общности)
был равен
, то теперь результат будет
, а если был равен {\displaystyle \sigma }
, то результат равен
. Так, мы получили ВП,
-вычисляющую {\displaystyle f}
, с той же длиной (количество инструкций не поменялось).
Примечание: если домножить вывод ВП на
справа, то очевидным образом получим ВП, {\displaystyle \sigma }
-вычисляющую функцию
.
Лемма 2: Если есть два ВП: -вычисляющая
и
-вычисляющая
с длинами
и
, где
и
— 5-цикличные перестановки, то существует ВП с 5-цикличной перестановкой
такая, что ВП
-вычисляет
, и ее размер не превосходит
+
.
Доказательство: Выложим «в ряд» инструкции четырех ВП: ,
, }
,
(строим обратные по лемме 1). Если одна или обе функции выдают 0, то результат большой программы {\displaystyle \varepsilon =id}
: например, при
. Если обе функции выдают 1, то
. Здесь
, что верно из-за того, что эти перестановки 5-цикличны (из-за неразрешимости группы симметрии {\displaystyle S_{5}}
). Длина новой ВП высчитывается по определению.
Доказательство теоремы
Будем доказывать по индукции. Предположим, что у нас есть схема C с входами и что для всех подсхем D и 5-цикличных перестановок {\displaystyle \sigma }
существует ВП,
-вычисляющая D. Покажем, что для всех 5-перестановок
существует ВП,
-вычисляющий C.
Размер итоговой ветвящейся программы не превосходит , где
— это глубина схемы. Если у схемы логарифмическая глубина, то у ВП полиномиальная длина.
Будем считать, что язык L принадлежит классу RP («randomized polynomial class» — случайный полиномиальный), если он допускается вероятностной машиной Тьюринга M, для которой выполнены следующие условия:
Примечание. Определение класса RP использует два понятия, которые не связаны между собой:
Примечание. Выбор в качестве порога ½ в данном случае не обязателен и данную константу можно заменить на другую (0 < {\displaystyle \epsilon } < 1). При этом RP будет содержать те же задачи, но языки, определяемые конкретными рандомизированными машинами Тьюринга, изменятся.
Если машина Тьюринга M отвечает «Да», то это гарантированно правда, в то время как «Нет» правда лишь в некоторых случаях. Класс сложности co-RP определяется аналогично, с той лишь разницей, что ответ «Нет» является гарантированной правдой, а «Да» не всегда. Класс BPP описывает алгоритмы, которые могут дать неправильный ответ в обоих случаях. Класс, являющийся пересечением RP и co-RP, называется ZPP.
Класс P является подмножеством класса RP, который, в свою очередь, является подмножеством класса NP. В том числе, P является подмножеством Co-RP, являющегося подмножеством Co-NP. При этом точно неизвестно, являются ли эти включения строгими. Большинство исследователей склоняется к версии, что P ≠ RP или RP ≠ NP, иначе P = NP (большинство ученых склоняется к тому, что это неправда). Также неизвестно, верно ли, что RP = Co-RP, и является ли RP подмножеством пересечения NP и Co-NP.
Ярким примером задачи, которая лежит в Co-RP, но неизвестно лежит ли она в P является задача проверки двух многочленов на равенство[en]: определить, является ли полиномиально выражение с несколькими целыми переменными тождественным нулем. Например, x · x − y · y − (x + y) · (x − y) — тождественный нуль, в то время как x · x + y · y — нет.
В теории вычислительной сложности ZPP (англ. zero-error probabilistic polynomial time — безошибочный вероятностный полиномиальный) — это класс задач с ответом «Да» либо «Нет», для которых существует вероятностная машина Тьюринга, удовлетворяющая следующим свойствам:
Существует альтернативный набор свойств:
Выбор одного из двух наборов свойств приводит к эквивалентным определениям класса ZPP. Машину Тьюринга, удовлетворяющую этим свойствам, иногда называют машиной Тьюринга типа Лас-Вегас.
Класс ZPP равен пересечению классов RP и Co-RP. Часто именно это принимается за определение ZPP. Чтобы продемонстрировать это, заметим, что любая задача принадлежащая одновременно RP и co-RP имеет алгоритм типа Лас-Вегас:
Заметим, что лишь один из алгоритмов A или B может дать неправильный ответ, и вероятность этого события равняется на каждом шаге 50 %. Таким образом, вероятность достигнуть k-го шага уменьшается экспоненциально относительно k. Это показывает, что математическое ожидание времени работы полиномиально. Из сказанного следует, что пересечение классов RP и co-RP содержится в ZPP.
Покажем, что ZPP содержится в пересечении RP и co-RP. Пусть имеется машина Тьюринга типа Лас-Вегас C, которая решает задачу. Обозначим математическое ожидание времени ее работы за M (по условию, оно конечно). Тогда можно построить следующий RP алгоритм:
Вероятность того, что ответ будет получен до момента останова, равняется ½ (из неравенства Маркова). Это в свою очередь означает, что вероятность ответа «Нет» при правильном ответе «Да» (такое могло случиться из-за преждевременной остановки C), равна ½, что удовлетворяет определению RP. Для доказательства включения ZPP в co-RP можно либо воспользоваться тем же рассуждением, либо заметить, что ZPP замкнут относительно взятия дополнения.
Исследование, описанное в статье про классы сложности алгоритмов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое классы сложности алгоритмов, класс сложности, класс ph, класс bqp, класс p, класс np класс bpp , класс l, класс nl, класс zpp , класс rp, класс nc и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов