Лекция
Привет, Вы узнаете о том , что такое a*, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое a*, а-стар, поиск пути , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
a* (произносится как « а-стар ») — это алгоритм обхода графа и поиска пути , который используется во многих областях компьютерных наук благодаря своей полноте, оптимальности и оптимальной эффективности При наличии взвешенного графа , исходного узла и целевого узла алгоритм находит кратчайший путь (относительно заданных весов) от источника до цели.
Одним из главных практических недостатков является его
Сложность пространства , где d — глубина самого поверхностного решения (длина кратчайшего пути от исходного узла до любого заданного целевого узла), а b — фактор ветвления (максимальное количество последователей для любого заданного состояния), поскольку он сохраняет все сгенерированные узлы в памяти. Таким образом, в практических системах маршрутизации путешествий он, как правило, уступает алгоритмам, которые могут предварительно обрабатывать граф для достижения лучшей производительности, , а также подходам с ограничением памяти; однако A* по-прежнему является лучшим решением во многих случаях.
Питер Харт , Нильс Нильссон и Бертрам Рафаэль из Стэнфордского исследовательского института (ныне SRI International ) впервые опубликовали алгоритм в 1968 году. Его можно рассматривать как расширение алгоритма Дейкстры . A* достигает лучшей производительности, используя эвристику для управления поиском.
По сравнению с алгоритмом Дейкстры, алгоритм A* находит только кратчайший путь от указанного источника до указанной цели, а не дерево кратчайших путей от указанного источника до всех возможных целей. Это необходимый компромисс для использования эвристики , направленной на конкретную цель . Для алгоритма Дейкстры, поскольку генерируется все дерево кратчайших путей, каждый узел является целью, и не может быть эвристики, направленной на конкретную цель.
A* был изобретен исследователями, работавшими над планированием пути робота Шейки.
A* был создан как часть проекта Shakey , целью которого было создание мобильного робота, который мог бы планировать свои собственные действия. Нильс Нильссон изначально предложил использовать алгоритм Graph Traverser для планирования пути Shakey. Graph Traverser руководствуется эвристической функцией h ( n ) , оценочным расстоянием от узла n до конечного узла: он полностью игнорирует g ( n ) , расстояние от начального узла до n . Бертрам Рафаэль предложил использовать сумму, g ( n )+ h ( n ) . Питер Харт изобрел концепции, которые мы сейчас называем допустимостью и согласованностью эвристических функций. A* изначально был разработан для поиска путей с наименьшей стоимостью, когда стоимость пути является суммой его стоимостей, но было показано, что A* можно использовать для поиска оптимальных путей для любой задачи, удовлетворяющей условиям алгебры стоимости.
Оригинальная статья A* 1968 года содержала теорему, утверждающую, что никакой алгоритм типа A* не может расширить меньше узлов, чем A*, если эвристическая функция согласована и правило разрешения конфликтов A* выбрано соответствующим образом. «Исправление» было опубликовано несколько лет спустя , утверждая, что согласованность не требуется, но это было показано ложным в 1985 году в окончательном исследовании оптимальности A* (теперь называемом оптимальной эффективностью) Дектера и Перла, которое дало пример A* с эвристикой, которая была допустимой, но не согласованной, расширяя произвольно больше узлов, чем альтернативный алгоритм типа A*.
Алгоритм поиска пути A*, перемещающийся по случайно сгенерированному лабиринту
Иллюстрация поиска A* для нахождения пути между двумя точками на графике. Слева направо все чаще используется эвристика, которая отдает предпочтение точкам, более близким к цели.
A* — это алгоритм информированного поиска или поиск по принципу «лучший первый» , то есть он сформулирован в терминах взвешенных графов : начиная с определенного начального узла графа, он стремится найти путь к заданному целевому узлу с наименьшей стоимостью (наименьшее пройденное расстояние, кратчайшее время и т. д.). Он делает это, поддерживая дерево путей, начинающихся в начальном узле, и расширяя эти пути по одному ребру за раз, пока не будет достигнут целевой узел.
На каждой итерации своего основного цикла A* необходимо определить, какой из своих путей следует расширить. Он делает это на основе стоимости пути и оценки стоимости, необходимой для расширения пути до цели. В частности, A* выбирает путь, который минимизирует
где n — следующий узел на пути, g ( n ) — стоимость пути от начального узла до n , а h ( n ) — эвристическая функция, которая оценивает стоимость самого дешевого пути от n до цели. Эвристическая функция специфична для проблемы. Если эвристическая функция допустима — то есть она никогда не переоценивает фактическую стоимость достижения цели — A* гарантированно вернет путь с наименьшей стоимостью от начала до цели.
Типичные реализации A* используют приоритетную очередь для выполнения повторного выбора узлов с минимальной (оцененной) стоимостью для расширения. Эта приоритетная очередь известна как открытое множество , край или граница . На каждом шаге алгоритма узел с наименьшим значением f ( x ) удаляется из очереди, значения f и g его соседей обновляются соответствующим образом, и эти соседи добавляются в очередь. Алгоритм продолжается до тех пор, пока удаленный узел (таким образом, узел с наименьшим значением f из всех узлов края) не станет целевым узлом. Значение f этой цели затем также является стоимостью кратчайшего пути, поскольку h в цели равно нулю в допустимой эвристике.
Описанный до сих пор алгоритм дает только длину кратчайшего пути. Чтобы найти фактическую последовательность шагов, алгоритм можно легко пересмотреть так, чтобы каждый узел на пути отслеживал своего предшественника. После запуска этого алгоритма конечный узел будет указывать на своего предшественника, и так далее, пока предшественник некоторого узла не станет начальным узлом.
Например, при поиске кратчайшего маршрута на карте h ( x ) может представлять собой расстояние по прямой до цели, поскольку это физически наименьшее возможное расстояние между любыми двумя точками. Для карты-сетки из видеоигры использование расстояния Taxicab или расстояния Чебышева становится лучшим вариантом в зависимости от набора доступных движений (4-х или 8-ми).
Если эвристика h удовлетворяет дополнительному условию h ( x ) ≤ d ( x , y ) + h ( y ) для каждого ребра ( x , y ) графа (где d обозначает длину этого ребра), то h называется монотонной или последовательной . С последовательной эвристикой A* гарантированно найдет оптимальный путь, не обрабатывая ни один узел более одного раза, и A* эквивалентно запуску алгоритма Дейкстры с уменьшенной стоимостью d' ( x , y ) = d ( x , y ) + h ( y ) − h ( x ) .
Иллюстрация поиска A* для нахождения пути от начального узла до конечного узла в задаче планирования движения робота . Пустые кружки представляют узлы в открытом наборе , т. е. те, которые еще предстоит исследовать, а заполненные кружки находятся в закрытом наборе. Цвет каждого закрытого узла указывает расстояние от цели: чем зеленее, тем ближе. Сначала можно увидеть, как A* движется по прямой в направлении цели, затем, столкнувшись с препятствием, он исследует альтернативные маршруты через узлы из открытого набора.
Пример алгоритма A* в действии, где узлы — это города, соединенные дорогами, а h(x) — это расстояние по прямой до целевой точки:
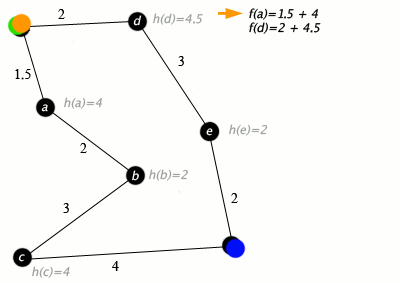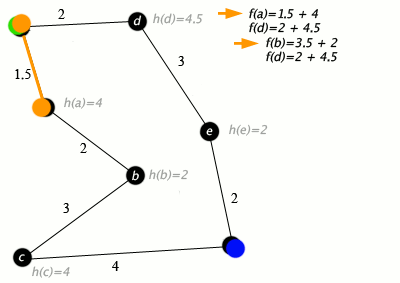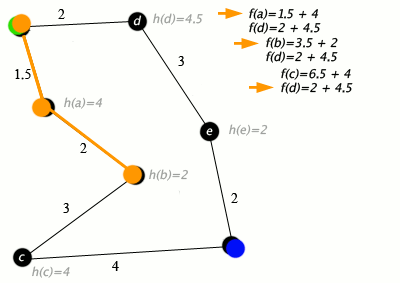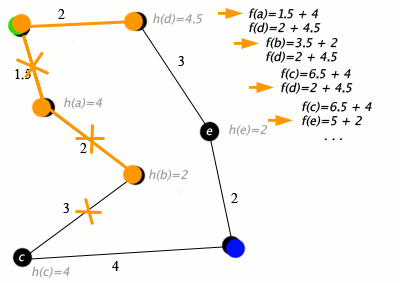
Обозначения: зеленый: начало; синий: цель; оранжевый: посещение
Алгоритм A* имеет реальные приложения. В этом примере ребра — это железные дороги, а h(x) — это расстояние по дуге большого круга (кратчайшее возможное расстояние на сфере) до цели. Алгоритм ищет путь между Вашингтоном, округ Колумбия, и Лос-Анджелесом.
Существует ряд простых оптимизаций или деталей реализации, которые могут существенно повлиять на производительность реализации A*. Первая деталь, которую следует отметить, заключается в том, что способ обработки приоритетной очередью связей может существенно влиять на производительность в некоторых ситуациях. Если связи разрываются, и очередь ведет себя в манере LIFO , A* будет вести себя как поиск в глубину среди путей с равной стоимостью (избегая исследования более одного одинаково оптимального решения).
Когда в конце поиска требуется путь, обычно для каждого узла сохраняется ссылка на родителя этого узла. В конце поиска эти ссылки можно использовать для восстановления оптимального пути. Если эти ссылки сохраняются, то может быть важно, чтобы один и тот же узел не появлялся в очереди приоритетов более одного раза (каждая запись соответствует другому пути к узлу, и каждая имеет свою стоимость). Стандартный подход здесь заключается в проверке того, появляется ли уже в очереди приоритетов узел, который должен быть добавлен. Если это так, то указатели приоритета и родителя изменяются, чтобы соответствовать пути с меньшей стоимостью. Стандартная двоичная куча на основе приоритетов напрямую не поддерживает операцию поиска одного из своих элементов, но ее можно дополнить хэш-таблицей , которая сопоставляет элементы с их положением в куче, позволяя выполнять эту операцию уменьшения приоритета за логарифмическое время. В качестве альтернативы куча Фибоначчи может выполнять те же операции уменьшения приоритета за постоянное амортизированное время .
Алгоритм Дейкстры , как еще один пример алгоритма поиска с равномерной стоимостью, можно рассматривать как частный случай A*, где 
для всех x .] Общий поиск в глубину может быть реализован с использованием A*, если учесть, что есть глобальный счетчик C, инициализированный очень большим значением. Каждый раз, когда мы обрабатываем узел, мы назначаем C всем его вновь обнаруженным соседям. После каждого назначения мы уменьшаем счетчик C на единицу. Таким образом, чем раньше обнаружен узел, тем выше его 
значение. И алгоритм Дейкстры, и поиск в глубину можно реализовать более эффективно без включения значение в каждом узле.
На конечных графах с неотрицательными весами ребер A* гарантированно завершается и является полным , т.е. он всегда найдет решение (путь от начала до цели), если оно существует. На бесконечных графах с конечным фактором ветвления и стоимостями ребер, которые отделены от нуля 
для некоторых фиксированныхε
), A* гарантированно завершится только в том случае, если существует решение.
Алгоритм поиска считается допустимым , если он гарантированно возвращает оптимальное решение. Если эвристическая функция, используемая A* , допустима , то A* допустим. Интуитивное «доказательство» этого таково:
Назовем узел закрытым, если он был посещен и не находится в открытом множестве. Мы закрываем узел, когда удаляем его из открытого множества. Основное свойство алгоритма A*, доказательство которого мы набросаем ниже, заключается в том, что когда н
закрыто, 
— это оптимистическая оценка (нижняя граница) истинного расстояния от начала до цели. Поэтому, когда узел цели, г
, закрыто, 
не больше истинного расстояния. Об этом говорит сайт https://intellect.icu . С другой стороны, оно не меньше истинного расстояния, поскольку оно есть длина пути к цели плюс эвристический термин.
Теперь мы увидим, что всякий раз, когда узел н закрыто, — оптимистическая оценка. Достаточно увидеть, что всякий раз, когда открытое множество не пусто, оно имеет по крайней мере один узел н на оптимальном пути к цели, для которой 
— истинное расстояние от начала, так как в этом случае + 
недооценивает расстояние до цели, и, следовательно, то же самое делает и меньшее значение, выбранное для закрытой вершины. Пусть 
— оптимальный путь от начала до цели. Пусть 
быть последним закрытым узлом на для которого 
— истинное расстояние от начала до цели (начало — одна из таких вершин). Следующий узел в имеет правильный значение, так как оно было обновлено, когда был закрыт, и он открыт, поскольку не закрыт.
Алгоритм A оптимально эффективен по отношению к набору альтернативных алгоритмов Alts на наборе задач P , если для каждой задачи P в P и каждого алгоритма A′ в Alts набор узлов, расширенный A при решении P, является подмножеством (возможно, равным) набора узлов, расширенного A′ при решении P. Окончательное исследование оптимальной эффективности A* принадлежит Рине Дехтер и Джуде Перл. [ Они рассмотрели множество определений Alts и P в сочетании с эвристикой A*, которая является просто допустимой или является как последовательной , так и допустимой. Самый интересный положительный результат, который они доказали, заключается в том, что A* с последовательной эвристикой оптимально эффективен по отношению ко всем допустимым алгоритмам поиска типа A* для всех «непатологических» задач поиска. Грубо говоря, их понятие непатологической задачи — это то, что мы теперь подразумеваем под «до разрешения конфликта». Этот результат не выполняется, если эвристика A* допустима, но не последовательна. В этом случае Дектер и Перл показали, что существуют допустимые алгоритмы типа A*, которые могут расширять произвольно меньше узлов, чем A*, на некоторых непатологических проблемах.
Оптимальная эффективность касается набора расширенных узлов, а не количества расширений узлов (количества итераций основного цикла A*). Когда используемая эвристика допустима, но не последовательна, возможно, что узел будет расширен A* много раз, экспоненциальное число раз в худшем случае. В таких обстоятельствах алгоритм Дейкстры может превзойти A* с большим отрывом. Однако более поздние исследования показали, что этот патологический случай возникает только в определенных надуманных ситуациях, когда вес ребра поискового графа экспоненциально зависит от размера графа, и что определенные непоследовательные (но допустимые) эвристики могут привести к уменьшению количества расширений узлов в поиске A*.
Поиск A*, который использует эвристику, которая в 5,0(=ε) раз больше последовательной эвристики , и получает неоптимальный путь
Хотя критерий допустимости гарантирует оптимальный путь решения, это также означает, что A* должен проверить все одинаково достойные пути, чтобы найти оптимальный путь. Чтобы вычислить приблизительные кратчайшие пути, можно ускорить поиск за счет оптимальности, ослабив критерий допустимости. Часто мы хотим ограничить это ослабление, чтобы гарантировать, что путь решения не хуже, чем (1 + ε ) раз от оптимального пути решения. Эта новая гарантия называется ε -допустимой.
Существует ряд ε -допустимых алгоритмов:
-оптимальные пути в целом.
.
.
-оптимально.
, где 0в противном случае
, и где 
— глубина поиска, а N — предполагаемая длина пути решения.
. использует две эвристические функции. Первая — это список FOCAL, который используется для выбора узлов-кандидатов, а вторая h F используется для выбора наиболее перспективного узла из списка FOCAL.
, где A и B — константы. Если не удается выбрать ни одного узла, алгоритм возвращается к функции 
, где C и D — константы.
, где 
, где λ и Λ — константы 
, π ( n ) является родительским узлом n , а ñ является последним расширенным узлом.Как эвристический алгоритм поиска, производительность A* во многом зависит от качества эвристической функции.
. Если эвристика близко приближается к истинной стоимости цели, A* может значительно сократить количество расширений узлов. С другой стороны, плохая эвристика может привести к множеству ненужных расширений.
В худшем случае A* расширяет все узлын
для которого 
, где
— стоимость оптимального целевого узла.
Предположим, что есть узел
в открытом списке 
, и это следующий узел, который будет расширен. Поскольку целевой узел имеет
, , целевой узел будет иметь меньшее значение f и будет расширен до .
Поэтому A* никогда не расширяет узлы с помощью
.
Предположим, что существует оптимальный алгоритм, который расширяет меньше узлов, в худшем случае с использованием той же эвристики. Это означает, что должен быть какой-то узел такой 
, однако алгоритм предпочитает не расширять его.
Теперь рассмотрим измененный график, где новое ребро стоимости
(
) добавляется к цели. Если 
, то новый оптимальный путь проходит через. Однако, поскольку алгоритм по-прежнему избегает расширения, он пропустит новый оптимальный путь, нарушив его оптимальность.
Следовательно, ни один оптимальный алгоритм, включающий A*, не может расширить меньше узлов, чемв худшем случае.
Худший случай сложности A* часто описывается как
, гдеб
является фактором разветвления и 
глубина самой поверхностной цели. Хотя это дает грубую интуицию, это не отражает точно фактическое поведение A*.
Более точная оценка учитывает количество узлов 
. Еслиεэто наименьшая возможная разница в 
-стоимость между отдельными узлами, то A* может расширяться до:
В худшем случае это отражает как временную, так и пространственную сложность.
Пространственная сложность A* примерно такая же, как и у всех других алгоритмов поиска по графу, поскольку он сохраняет все сгенерированные узлы в памяти. На практике это оказывается самым большим недостатком поиска A*, что приводит к разработке эвристических поисков с ограничением памяти, таких как итеративное углубление A* , ограниченный памятью A* и SMA* .
A* часто используется для решения общей проблемы поиска пути в таких приложениях, как видеоигры, но изначально он был разработан как общий алгоритм обхода графа. Он находит применение в различных задачах, включая задачу синтаксического анализа с использованием стохастических грамматик в обработке естественного языка . Другие случаи включают информационный поиск с онлайн-обучением.
Отличие A* от жадного алгоритма поиска по лучшему первому заключается в том, что он учитывает стоимость/пройденное расстояние g ( n ) .
Некоторые распространенные варианты алгоритма Дейкстры можно рассматривать как частный случай A*, где эвристикач
для всех узлов; в свою очередь, и Дейкстра, и A* являются частными случаями динамического программирования . Сам A* является частным случаем обобщения ветвей и границ .
A* похож на лучевой поиск , за исключением того, что лучевой поиск сохраняет ограничение на количество путей, которые он должен исследовать.
A* также можно адаптировать к алгоритму двунаправленного поиска , но необходимо уделить особое внимание критерию остановки.
Исследование, описанное в статье про a*, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое a*, а-стар, поиск пути и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов