Лекция
Привет, сегодня поговорим про от алгоритма к структуре данных, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое от алгоритма к структуре данных , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.
" Создается впечатление, что на примерах сортировок можно построить целый курс программирования. "
Никлаус Вирт
" Боюсь, что не сумею вам все это объяснить, - учтиво промолвила Алиса. - Я и сама ничего не понимаю. Столько превращений в один день хоть кого собьет с толку. "
Льюис Кэрролл
Постановка задачи, как правило, оставляет программисту возможность выбора пути для ее решения. Свидетельством тому служит разнообразие алгоритмических механизмов, включая не только упомянутые нами выше, но и некоторые другие. Возникают ли сомнения в том, что они должны входить в арсенал программиста?
Для начала вспомним что такое структуры данных и алгоритмы и какие они бывают?
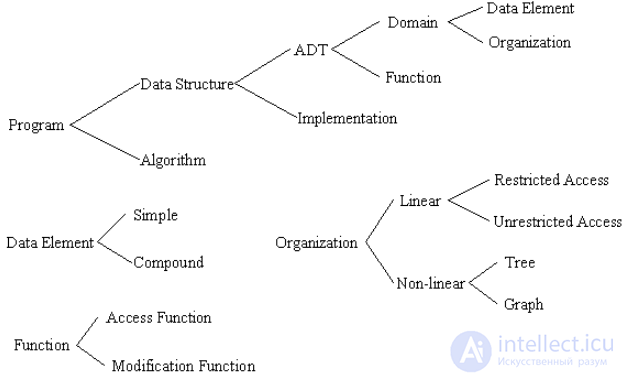
Что такое структуры данных?
Существют разные определения этого понятия.
Существует несколько общих структур данных: массивы, связанные списки, очереди, стеки, двоичные деревья, хеш-таблицы, графики и т. д. Эти структуры данных можно классифицировать как линейные или нелинейные структуры данных в зависимости от того, как данные концептуально организованы или агрегированы. .
Линейные структуры. К этой категории относятся массив, список, очередь и стек. Каждый из них представляет собой коллекцию, в которой свои записи хранятся в линейной последовательности, и в которую записи могут быть добавлены или удалены по желанию. Они различаются ограничениями, которые они накладывают на то, как эти записи могут быть добавлены, удалены или доступны. Общие ограничения включают FIFO и LIFO.
Нелинейные структуры. Деревья и графы - классические нелинейные структуры. Записи данных располагаются не в последовательности, а по разным правилам.
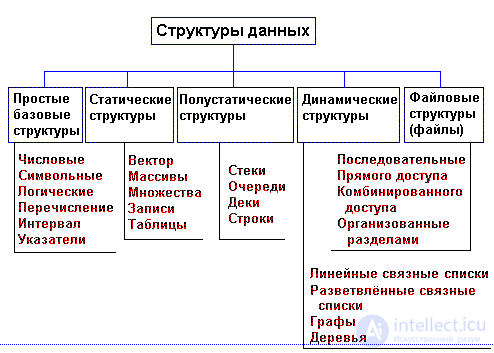
Рис. 1.1. Классификация структур данных
Что такое абстрактные типы данных (ADT)?
Помните цель разработки программного обеспечения? Надежность, адаптируемость и возможность повторного использования . Благодаря этим усилиям по написанию лучшего кода возникла новая метафора для использования и построения структур данных: абстрактный тип данных , который подчеркивает понятие абстрактности .
Когда мы говорим «тип данных», мы часто ссылаемся на примитивные типы данных, встроенные в язык, такие как целые, вещественные, символьные и логические. Целое число, скорее всего, реализовано или представлено в компьютере четырьмя байтами. Однако, когда мы используем целые числа, мы совершенно не беспокоимся о его внутреннем представлении или о том, как эти операции реализуются компилятором в машинном коде. Кроме того, мы знаем, что даже когда мы запускаем нашу программу на другом компьютере, поведение целого числа не меняется, даже если его внутреннее представление может измениться. Что мы знаем, так это то, что мы можем использовать примитивные типы данных через их рабочий интерфейс - '+', '-', '*' и '/' для целых чисел. Примитивные типы данных были абстрактными записями.
Стек или очередь - это пример ADT. Как стеки, так и очереди могут быть реализованы с использованием массива. Также возможно реализовать стеки и очереди, используя связанные списки. Это демонстрирует «абстрактный» характер стеков и очередей: как их можно рассматривать отдельно от их реализации.
Применяя идею абстракции к структурам данных, у нас есть ADT для структур данных. С одной стороны, ADT четко разделяет интерфейс и реализацию , пользователь видит только интерфейс и, следовательно, не должен вмешиваться в реализацию. С другой стороны, если реализация ADT изменится, код, который использует ADT, не сломается, поскольку интерфейс останется прежним. Таким образом, абстракция делает код более надежным и простым в обслуживании . Более того, как только ADT построен, его можно использовать несколько раз в различных контекстах. Например, ADT списка может использоваться непосредственно в коде приложения или может использоваться для построения другого ADT, такого как стек.
Как мне выбрать правильные структуры данных?
При написании программы одним из первых шагов является определение или выбор структур данных. Каковы «правильные» структуры данных для программы? Интерфейс операций , поддерживаемой структура данных является одним из факторов , которые следуют учитывать при выборе между несколькими доступными структурами данных. Еще одним важным фактором является эффективность структуры данных: сколько места занимает структура данных и каково время выполнения операций в ее интерфейсе?
Что такое алгоритм?
Есть много определений алгоритмов. Алгоритм - это процедура, конечный набор четко определенных инструкций для решения проблемы, которая при заданном начальном состоянии завершается в определенном конечном состоянии . Вычислительная сложность и эффективная реализация алгоритма важны для вычислений, и это зависит от подходящих структур данных.
Классификация алгоритмов по структуре:
Классификация алгоритмов в зависимости от ассимтотической сложности
Классификация конструктивных приемов :
Способы представления алгоритма : существует множество различных способов выразить алгоритм, включая естественный язык, псевдокод, блок-схемы и языки программирования. Выражения алгоритмов на естественном языке имеют тенденцию быть многословными и неоднозначными и редко используются для сложных или технических алгоритмов. Псевдокод и блок-схемы - это структурированные способы выражения алгоритмов, которые позволяют избежать многих двусмысленностей, характерных для операторов естественного языка, оставаясь при этом независимыми от конкретного языка реализации. Языки программирования в первую очередь предназначены для выражения алгоритмов в форме, которая может выполняться компьютером, но часто используются как способ определения или документирования алгоритмов.

Эффективность программы: время vs. Об этом говорит сайт https://intellect.icu . пространство. Интересно знать, сколько определенного ресурса (например, времени или хранилища) требуется для данного алгоритма. Были разработаны методы для анализа алгоритмов , чтобы получить такие количественные ответы, такие как большая нотация O . Например, время, необходимое для обхода массива из n слотов, пропорционально n , и мы говорим, что время имеет порядок O ( n ). Однако для доступа к i- му элементу в массиве требуется только постоянное время, которое не зависит от размера массива, поэтому имеет порядок O (1).
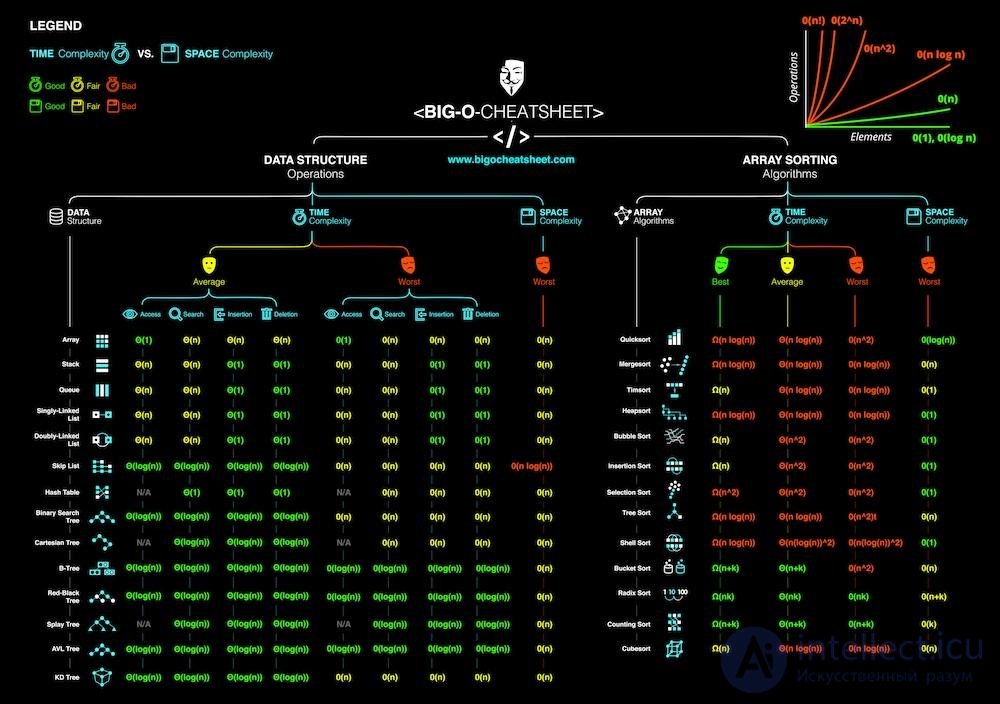
В самом деле, "сходу" написанная программа вполне может оказаться неэффективной. Но всякий ли программист удосуживается выяснить это? К сожалению, с характерными примерами "скрытой" неэффективности нам неоднократно приходилось сталкиваться, обсуждая с юными кодировщиками предложенные ими алгоритмические и программные решения. Наиболее популярны при этом доводы, что готовая программа, во-первых, работает, во-вторых, работает быстро, и вообще, мол, "чего вы от меня (или от нее, то бишь, программы) хотите".
Действительно, представленный продукт выглядит работоспособным, и трудно убедить кодировщика, что ему стоит поразмыслить еще. Дело в том, что уровень сложности учебных задач, с которыми начинающим программистам приходится иметь дело, не слишком высок. Если приходится строить алгоритм полиномиальной сложности, то обычно она не превышаетO(n2), в крайнем случае, O(n3). А мы уже знаем, что при небольших значениях n реальное время выполнения такого вычислительного процесса не дает повода для поисков лучшего решения. В то же время, подготовкой сколько-нибудь значительного набора данных, с целью проверки поведения программы при больших n, те же программисты себя не утруждают. Что касается сложности экспоненциальной, то таких задач в учебном плане, - мы имеем ввиду обыкновенный школьный курс информатики, - довольно мало, если они вообще представлены.
Итак, будем исходить из необходимости включить в "джентльменский набор" программиста как можно большее число базовых алгоритмов. Говоря "как можно больше", мы не планируем просто перенумеровать их, а затем, в порядке очередности, обсуждать. Все же целесообразно провести некоторую их классификацию.
С одним из вариантов подобной классификации вам пришлось столкнуться уже на раннем этапе знакомства с дисциплиной программирования. Имеется ввиду предваряющая алгоритмику классификация программных механизмов по типам - линейный алгоритм, ветвление и цикл.
Разумеется, обсуждение эффективности только начинается с появлением циклической обработки. И нам надо идти дальше. Заманчивой выглядит идея Вирта, вынесенная в эпиграф. Но цель, которую мы преследуем в этом разделе, гораздо скромнее: мы не замахиваемся на "целый" курс, а хотим лишь продемонстрировать различия в алгоритмическом содержании задач, возникающих перед программистом. Что нам мешает проделать нечто подобное - или хотя бы попытаться - на основе объекта, знакомого любому читателю, - таблицы умножения!? Итак, предлагаем отнестись к дальнейшим рассуждениям как к некоему развернутому упражнению по конструированию алгоритмов.
Естественно, прежде чем обратиться к таблице, следует поставить задачу. Примем следующую формулировку: "вычислить по входным значениям пары натуральных чисел соответствующее выходное значение - их произведение". На ключевое слово "вычислить" обратите внимание: его присутствие отражается в том, как построен следующий
Алгоритм 1. Умножение 1
Вернувшись на сколько-то лет назад, каждый из нас вспомнит, как его учили решать эту задачу в первом классе. Предположим, в порядке обсуждения, что входной тест включает числа 5 и 6 (очевидно, годится и любая другая пара однозначных чисел).
Возьмем кучку из 5 спичек; добавим к ним еще 5 из второй кучки; затем еще пять из третьей; и так далее, пока не соберем спички из всех 6 кучек вместе. Сколько всего у нас получилось спичек? Возможно, для умножения 5×6 вам предлагали в детстве интерпретацию "5 куч по 6 спичек", но автора учили именно так, - впрочем, сути это не меняет (рис. A4-1).

Рис. 1
Такое объяснение, или нечто в том же роде, описывает алгоритм умножения двух сомножителей - первого на второй - в классе натуральных чисел. Трудоемкость этого алгоритма составляет O(n), где n - второй сомножитель.
Алгоритм 2. Умножение 2
Несколько больше проблем вызовет ситуация большого числа кучек (пусть в новом примере их 26) и спичек в них (по 15 в каждой). Теперь уместно вспомнить алгоритм умножения "в столбик".
Рис. 2
Умножая здесь 6 на 15, по ходу вычислений мы должны умножить 6 на 5 (или 5 на 6), что позволяет свести многие шаги алгоритма A4-2 к вызовам Алгоритма 1. Можно предположить, что в свое время этот вариант алгоритма был одним из первых опытов читателя в применении метода сведения задачи к подзадачам.
Алгоритм 3. Умножение 3
Чем нас не устраивает - или может не устроить при наличии лучшего решения — Алгоритма 2? Естественно, многократными вызовами Алгоритма 1, чья эффективность сомнительна. Здесь-то, наконец, нам и пригодится таблица умножения.
Значение, которое постановка задачи предлагает вычислить, таблицей предоставляется непосредственно - на пересечении 5-й строки и 6-го столбца. Все бы хорошо, но остальные строки и столбцы оказываются "лишними", создавая проблему выбора именно той пары, которая нужна. Так возникают две однотипные подзадачи (вновь: декомпозиция!) - поиска 5-й, сверху, строки и, после этого, поиска в ней 6-го слева числа (рис. A4-3).
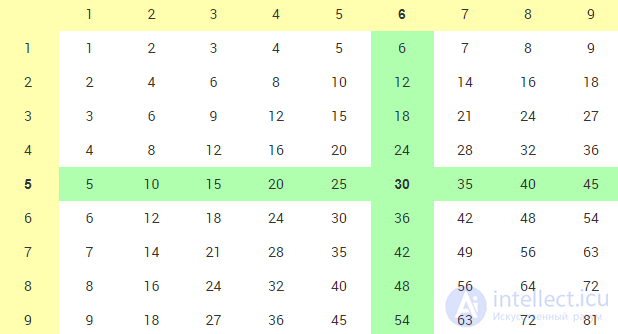
Рис. 3
Такой поиск отнюдь не является примитивной операцией. Он требует циклической обработки кандидатов в определенной последовательности - в нашем случае, перебор и проверку строк с 1-й по 5-ю, затем столбцов с 1-го по 6-й. Легко заметить, что очередность кандидатов в последовательности может быть установлена и иначе: скажем, от нижней строки - вверх и, затем, от правого крайнего столбца - влево. Но характер этих отличий лишь технический, они никак не влияют на оценку трудоемкости перебора входящих в последовательность элементов.
Нас же, разумеется, интересует алгоритмическое отличие. Принципиально иначе работает метод "разделяй и властвуй", хотя здесь мы его только упомянем, оставляя обсуждение механизма на будущее.
Таким образом, в нашей классификации надо предусмотреть место не единственному в своем роде механизму -последовательному поиску, а целому семейству алгоритмов поиска, в котором, кстати, есть и другие представители помимо двух уже упомянутых. Вот и технология поиска в таблице - в данном случае - разбивается на две самостоятельных подзадачи поиска в линейном массиве.
Вернемся еще раз к исходной постановке задачи. Оказывается, мы ее "незаметно" подменили - как только появилась таблица. Фактически, модификация формулировки связана с замещением ключевого слова "вычислить" словом "найти". То есть соответствующая постановка задачи, как только ее дополнили подходящей структурой данных, сразу подсказала нам иное алгоритмическое решение. О структурах данных мы поговорим ниже, а пока попробуем развить это соображение дальше.
Алгоритм 4. Умножение 4
Так, если мы расширим стандартную таблицу умножения до 15 строк и 26 столбцов, то интересующее нас произведение обнаружим в нижнем правом ее углу (рис. A4-4).

Рис. 4
По существу, постановка задачи и знакомство с Алгоритмом 3 продиктовали выбор структуры, а входные данные определили значения параметрам структуры.
Конечно, не всякое алгоритмическое решение стоит принимать, - но мы ведь пока только рассуждаем, а не кинулись сходу писать программный код. И здесь несложные рассуждения показывают, что Алгоритм 4 нас нас вряд ли устроит. Действительно, с ростом числа строк m и столбцов n - то есть значений входных параметров - размеры таблицы должны быть никак не меньше произведения указанных величин. Приходится вспоминать о емкостной сложности алгоритма, которая связана с хранениеминформации в выбранной структуре данных, и составит O(m·n).
Рассуждая далее, замечаем, что и с временнОй сложностью возникают проблемы. Мало выделить память под структуру; чтобы хранить данные, сначала надо их там разместить, а на это также потребуется время порядка O(m·n). Кстати, начальное размещение данных в выбранной структуре часто называют ее инициализацией. Итак, при однократном вычислении произведения 15×26, последний алгоритм нас не устраивает сразу по двум причинам: из-за неффективности расхода времени на этапе инициализации и из-за емкостной неффективности выбранной структуры.
Естественно, те же рассуждения актуальны для любой пары значений сомножителей. Как быть: ведь задачу умножения натуральных чисел приходится решать регулярно? В некомпьютерной практике (микрокалькуляторы - не в счет) мы нередко пользуемся двумя альтернативными алгоритмами, переключаясь в нужные моменты. Механизм заключается в том, чтобы числа с разрядностью более 1 перемножать в столбик, согласно Алгоритму 2, а для поразрядных операций обращаться к таблице умножения из Алгоритма 3. При таком подходе хранимая "в уме" - но в детстве инициализированная! - таблица умножения имеет привычные размеры 10×10 (или 9×9), и до Алгоритма 4 дело не доходит.
Однако на размерах таблицы 10×10 свет клином не сошелся. Читателю, наверно, любопытно узнать, что австралийские школьники "зубрят" таблицу 13×13. Стало быть, и здесь есть место выбору. Ну, а при компьютерной обработке, когда используется двоичная система счисления, таблица становится совсем небольшой - 2×2. Есть ли смысл инициализировать ее в оперативной памяти, или используются иные алгоритмы, мы обсудим в Главе B, где пойдет речь о компьютерной арифметике.
Впрочем, не станем отвлекаться. Надеюсь, читатель не забыл, что наша цель - обрисовать круг задач и алгоритмов, встречающихся в практике программирования и, естественно, в нашем курсе. А таблица умножения служит нам "всего лишь" модельным объектом. Зато в нашу классификацию добавляется еще один метод решения задач - это компьютерное моделирование. Точнее, моделирование численное, при котором компьютер служит быстродействующим исполнителем и демонстратором результатов обработки. Глубоко вторгаться в эту самостоятельную область информатики мы не намерены, ограничимся лишь одним примером. Имеем ввиду визуализаторы алгоритмов, которых в нашем курсе немало. В самом деле, это всего лишь модели, и применение их для реализации - в полном объеме - возможностей и целей соответствующих алгоритмов отнюдь не предусмотрено.
Обратим теперь внимание, что в рассмотренных алгоритмах мы учитываем - пусть иногда и неявно, но при кодировании, безусловно, в явном виде - форму представления информации. Так, говоря о данных, мы всюду как-то их типизировали, например, в Алгоритме 1 относя к натуральным числам. Что уж говорить о машинной арифметике, где форма, в значительной степени, диктует алгоритмы обработки.
Для представления данных мы также воспользовались термином "структура", не уточняя содержание, поскольку читатель встречался с этим понятием в языке программирования. В алгоритмике структуры данных понимают несколько шире, чем в конкретном языке программирования, но общие характеристики понятий совпадают. Во всяком случае, имеется ввиду конечная совокупность элементов, связанных - внутри структуры - неким порядком. Установленный порядок дает возможность различать элементы структуры по месту расположения в ней или относительно друг друга.
Язык программирования может допускать или не допускать манипулирование всей структурой как целым, но всегда допускает обработку составляющих ее элементов в отдельности. В алгоритмике актуальны обе возможности. Каждой обрабатываемой структуре приписывается ее собственный набор операций, и в этом смысле возможности языка обычно уже. Так, отдельныеалгоритмические операции нередко приходится эмулировать последовательностью операций, допускаемых рамками языка. Подробно эти вопросы также ждут своего обсуждения, - мы перейдем к нему, начиная с Главы D.
В указанном смысле при обработке таблицы умножения разрешены операции - и, соответственно, регламентированы механизмы их реализации - прямого обращения к строке или столбцу по заданному номеру, запись значения элемента таблицы при ее инициализации, чтение элемента.
Упражнение 1 Возможно, Ваше знакомство с ЭВМ до сих пор не требовало знания устройства оперативной памяти. В таком случае, выясните, что собой представляет оперативная память как структура (размещения) данных.
Упражнение 2 Если мы задумаемся о способе хранения таблицы умножения, то, вероятно, решим, что нужны еще какие-то операции. Какие?
Наконец (а возможно, с этого следовало как раз начинать), объединение элементов в структуру требует, чтобы они обладали неким - по крайней мере, одним - общим свойством. В нашей модельной задаче этим признаком является принадлежность элементов к классу натуральных чисел.
Упражнение 3 Можно ли рассматривать ряд натуральных чисел в качестве структуры данных?
Упражнение 4 На какой структуре данных вы остановились бы при описании воинского подразделения на параде?
Представим, что в ячейках таблицы умножения, помимо цифрового значения, разместили также и его словесное обозначение, например, "30, thirty". Этот вариант мог бы нам пригодиться, скажем, как методическое пособие при обучении числительным английского языка. Тогда значением элемента структуры является вся запись "30, thirty", ключом записи будет "30", а информационная часть - "thirty" - доступна по ключу.
Для выбранного представления понятия ключ и номер (или индекс) элемента не являются взаимозаменяемыми. Назначение ключа - в идентификации элемента структуры, назначение индекса - обеспечивать доступ к элементу. Так, в таблице на рис. A4-3 ключи присутствуют в явном виде: в левом столбце размещены ключи строк, а в верхней строке - ключи столбцов. Номера же строк и столбцов связаны со способом отображения структуры на конкретном носителе. Например, вполне можно левый столбец и верхнюю строку убрать из той же таблицы, оставив ее без ключей.
Здесь внимательный читатель может упрекнуть нас в различном применении понятия элемент при рассмотрении примеров. Действительно, то мы понимаем под элементом строку (или столбец), то элемент лежит на их пересечении. Фактически, таблица из строк, таблица из столбцов и "просто" таблица умножения лишь внешне, на книжной странице, выглядят одинаково, но, с точки зрения доступа, они различны. Различие определяется уже типом составляющих структуры элементов. Но не только им. Соответственно, речь идет о разных структурах, и манипулировать этими тремя таблицами придется также по-разному.
Упражнение 5 Какой из трех вариантов целесообразнее с точки зрения применения "по назначению" при размещении таблицы в памяти ЭВМ?
Упражнение 7 Поскольку нас, в не меньшей степени, будет интересовать возможность отображения и других структур данных в памяти ЭВМ, то полезно вспомнить, как располагаются в памяти компьютера данные, описываемые в языке программирования как составные.
Упражнение 8 Напишите программу "изучения английских числительных по таблице умножения". Используйте язык программирования, а не электронные таблицы. Но ваша программа может работать по принципу электронной таблицы.
В заключение могу сказать, что, к сожалению, нет никакой возможности «сократить» путь. Ты можешь просто погрузиться с головой в эти темы. Начать писать код, заниматься его отладкой, читать правильный код других людей, чтобы понять, где, как и почему сами свернули не туда. Это сложно, но с каждой новой попыткой твои навыки будут расти, а по мере их роста все станет проще и понятнее.
К сожалению, в одной статье не просто дать все знания про от алгоритма к структуре данных. Но я - старался. Если ты проявишь интерес к раскрытию подробностей,я обязательно напишу продолжение! Надеюсь, что теперь ты понял что такое от алгоритма к структуре данных и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Алгоритмы и теория алгоритмов
Термины: Алгоритмы и теория алгоритмов