Порядок роста сложности алгоритмов кратко

Привет, сегодня поговорим про порядок роста сложности, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое порядок роста сложности, классы сложности алгоритмов, сложность алгоритм , настоятельно рекомендую прочитать все из категории Алгоритмы и теория алгоритмов.

1 Порядок роста алгоритмов и их классификация.

Точное знание количества операций, выполненных алгоритмом, не играет существенной роли в анализе алгоритмов. Куда важнее скорость роста этого числа при росте объема входных данных. Эта скорость называется порядком роста алгоритма. Нас интересует только общий характер поведения алгоритмов, а не подробности этого поведения. При анализе алгоритмов нас скорее будет интересовать класс порядка роста, к которому относится алгоритм, чем точное количество выполняемых им операций каждого типа (табл. 2.1).

Быстрорастущие функции доминируют над функциями с медленным ростом. Поэтому если было выявлено, что порядок роста алгоритма является суммой двух или нескольких функций, то часто отвергаются все функции кроме тех, которые растут быстрее всего. Если, например, установлено, что алгоритм делает сравнений, то говорится, что порядок роста алгоритма равен.

Таблица 2.1 – Некоторые классы порядков роста

Количество элементов входа алгоритма
1	O(1)	O(1)	O(1)	O(1)	O(1)	O(2)
10	3	10	33	100	1000	1024
20	4	20	86	400	8000	1048576
50	6	50	282	2500	125000
100	7	100	664	10000	1000000

Скорость роста сложности алгоритма играет важную роль, и определяется старшим, доминирующим членом формулы.

Хотя в анализе алгоритмов к одному классу относят все функции, порядок роста которых совпадает до постоянного множителя, существует множество подобных классов. Например, порядок роста функции зависит от . Временную эффективность большого количества алгоритмов можно отнести к одному из нескольких основных классов (табл. 2.2).

Таблица 2.2 – Перечень основных классов алгоритмов в зависимости от временной эффективности

Класс	Название	Комментарий
1	константный	Если не учитывать эффективность алгоритмов в лучшем случае, к этому классу попадает очень небольшое количество алгоритмов.Обычно, при увеличении размера входных данных, увеличивается и время выполнения алгоритма.
log n	логарифмический	Обычно такая зависимость появляется в результате сокращения размера задачи на постоянное значение на каждом шаге итерации алгоритма. Об этом говорит сайт https://intellect.icu . В логарифмическом методе невозможна работа со всеми входными данными (и даже с некоторой их фиксированной частью). В этом случае время выполнения любого алгоритма будет находиться минимум в линейной зависимости от размера входных данных.
n	линейный	К этому классу относятся алгоритмы, выполняющие сканирование списка, состоящего из элементов, например, алгоритм поиска путем последовательного перебора.
n log n	n log n	К этому классу относится большинство алгоритмов декомпозиции, такие как алгоритмы сортировки слиянием или быстрой сортировки
n^2	квадратичный	Как правило, подобная зависимость характеризует эффективность алгоритмов, содержащих два встроенных циклы. В качестве типичных примеров достаточно назвать простой алгоритм сортировки и целый ряд операций, выполняемых над матрицами.
n^3	кубический	Как правило, подобная зависимость характеризует эффективность алгоритмов, содержащих три встроенных цикла. К этому классу относятся несколько довольно сложных алгоритмов линейной алгебры.
2^n	экспоненциальный	Данная зависимость типична для алгоритмов, выполняющих обработку всех подмножеств некоторого множества, которая состоит из элементов. Часто термин «экспоненциальный» используется в широком смысле и означает очень высокие порядки роста, т.е. включая более быстрые по сравнению сэкспоненциальным, порядки роста.
n!	факториальная	Данная зависимость типична для алгоритмов, выполняющих обработку всех перестановок некоторого множества, которая состоит из элементов.

2. Асимптотический анализ алгоритмов.

Рассматривая входные данные достаточно больших размеров для оценки только такой величины, как порядок роста времени работы алгоритма, мы определяем асимптотическую эффективность алгоритмов. Это означает, что нас интересует только то, как время работы алгоритма растет с увеличением размера входных данных до бесконечности. Обычно алгоритм, эффективный в асимптотическом смысле, будет продуктивным для всех входных данных, за исключением очень маленьких.

Для того чтобы можно было сравнивать между собой эти порядки роста и классифицировать их, были введены условные обозначения:

O(n) (произносится как «О большое»),

Θ(n) («тетабольшое»)

Ω(n) («омега большое»).

Обозначим через t(n) время выполнения алгоритма. Через g(n) обозначим Функции t(n) и g(n) могут быть любыми неотрицательными функциями, определенными на множестве натуральных чисел.

Говоря нестрого, обозначение O(g(n)) – это множество всех функций, порядок роста которых при достаточно больших не превышает (т.е. меньше или равен) значения некоторой константы, умноженной на значение функции g(n) .

Второе обозначение Ω(g(n)) , – это множество всех функций, порядок роста которых при достаточно больших не меньше (т.е. больше или равен) значения некоторой константы, умноженной на значение функции g(n) .

Наконец, обозначение Θ (g(n)) – это множество всех функций, порядок роста которых при достаточно больших равен значению константы, умноженной на значение функции g(n) .

3 Основные определения.

Основным показателем сложности алгоритма является время, необходимое для решения задачи и объем требуемой памяти.

Также при анализе сложности для класса задач определяется некоторое число, характеризующее некоторый объем данных – размер входа.

Итак, можем сделать вывод, что сложность алгоритм а – функция размера входа.

Сложность алгоритма может быть различной при одном и том же размере входа, но различных входных данных.

Существуют понятия сложности в худшем, среднем или лучшем случае. Обычно, оценивают сложность в худшем случае.

Временная сложность в худшем случае – функция размера входа, равная максимальному количеству операций, выполненных в ходе работы алгоритма при решении задачи данного размера.

Ёмкостная сложность в худшем случае – функция размера входа, равная максимальному количеству ячеек памяти, к которым было обращение при решении задач данного размера.

порядок роста сложности (или аксиоматическая сложность) описывает приблизительное поведение функции сложности алгоритма при большом размере входа. Из этого следует, что при оценке временной сложности нет необходимости рассматривать элементарные операции, достаточно рассматривать шаги алгоритма.

Шаг алгоритма – совосовокупность последовательно-расположенных элементарных операций, время выполнения которых не зависит от размера входа, то есть ограничена сверху некоторой константой.

Ниже приведен список некоторых наиболее часто используемых обозначений Big O и их сравнение производительности с различными размерами входных данных.

Сложность операций структуры данных

Сложность алгоритмов сортировки массивов

Обозначение Big O

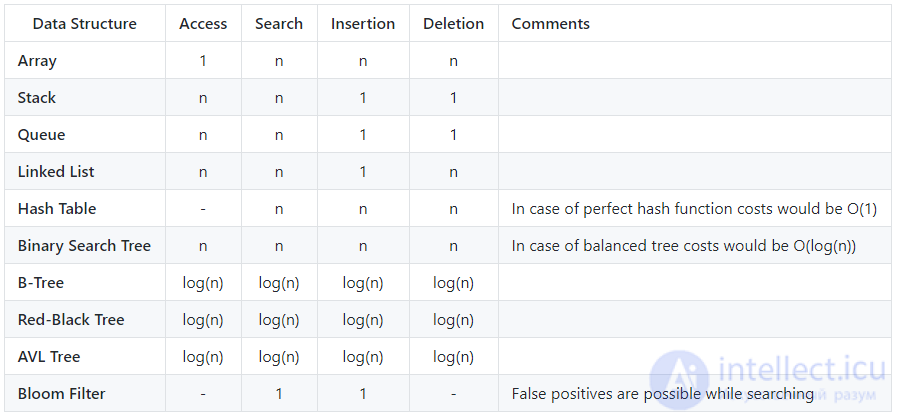
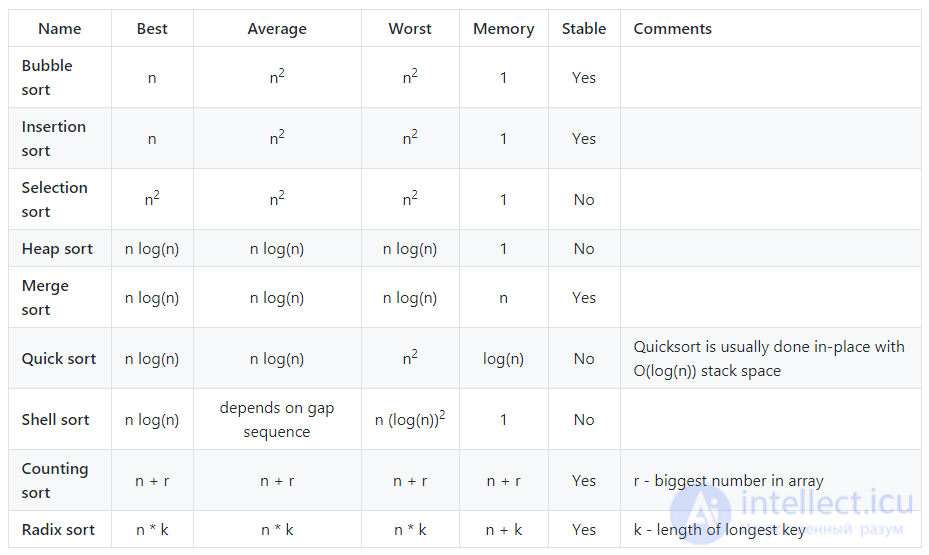
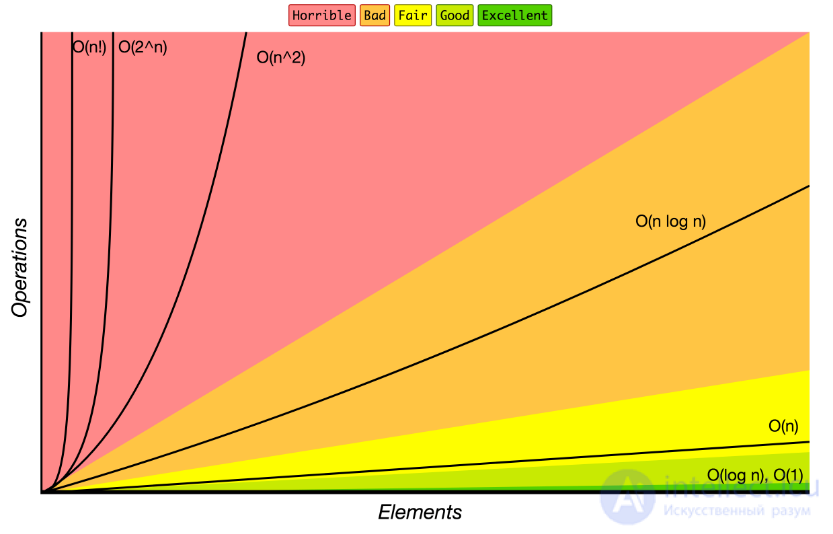
Обозначение Big O используется для классификации алгоритмов в соответствии с тем, как растут их требования к времени выполнения или месту при увеличении размера входных данных. На графике ниже вы можете найти наиболее распространенные порядки роста алгоритмов, указанных в обозначениях Big O.

Вау!! 😲 Ты еще не читал? Это зря!

• алгоритм
• асимптотический анализ алгоритмов

На этом все! Теперь вы знаете все про порядок роста сложности, Помните, что это теперь будет проще использовать на практике. Надеюсь, что теперь ты понял что такое порядок роста сложности, классы сложности алгоритмов, сложность алгоритм и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмы и теория алгоритмов

Из статьи мы узнали кратко, но содержательно про порядок роста сложности